高中数学高考2022届高考数学一轮复习(新高考版) 第3章 §3 2　导数与函数的单调性课件PPT

这是一份高中数学高考2022届高考数学一轮复习(新高考版) 第3章 §3 2　导数与函数的单调性课件PPT，共60页。PPT课件主要包含了考试要求，内容索引，主干梳理基础落实，题型突破核心探究，课时精练，单调递增，单调递减，常数函数，题组一思考辨析，1＋∞等内容，欢迎下载使用。
1.结合实例，借助几何直观了解函数的单调性与导数的关系.2.能利用导数研究函数的单调性，会求函数的单调区间(其中多项式 函数一般不超过三次).
ZHUGANSHULI JICHULUOSHI
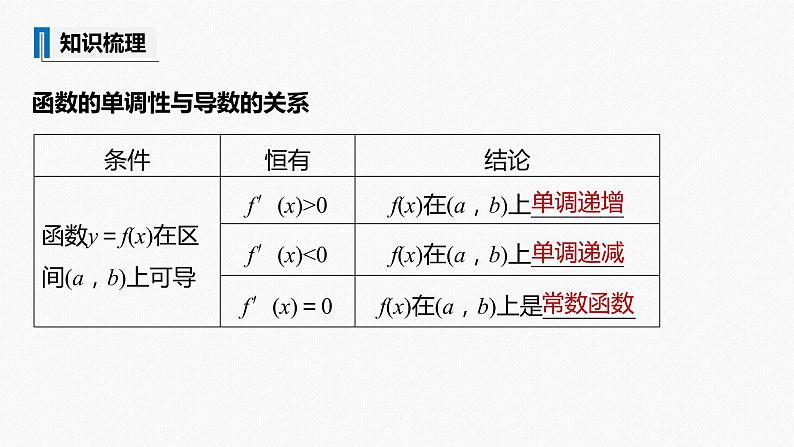
函数的单调性与导数的关系
1.“f′(x)>0在(a，b)上成立”是“f(x)在(a，b)上单调递增”的什么条件？
提示　若f(x)在(a，b)上单调递增，则f′(x)≥0，所以“f′(x)>0在(a，b)上成立”是“f(x)在(a，b)上单调递增”的充分不必要条件.
2.若函数f(x)在区间(a，b)上存在递增区间，则在区间(a，b)上，f′(x)应满足什么条件？
提示　若f(x)在(a，b)上存在递增区间，则当x∈(a，b)时，f′(x)>0有解.
1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)如果函数f(x)在某个区间内恒有f′(x)＝0，则f(x)在此区间内没有单调性.(　　)(2)在(a，b)内f′(x)≤0且f′(x)＝0的根有有限个，则f(x)在(a，b)内单调递减.(　　)(3)若函数f(x)在定义域上都有f′(x)>0，则f(x)在定义域上一定单调递增.(　　)(4)函数f(x)＝x－sin x在R上是增函数.(　　)
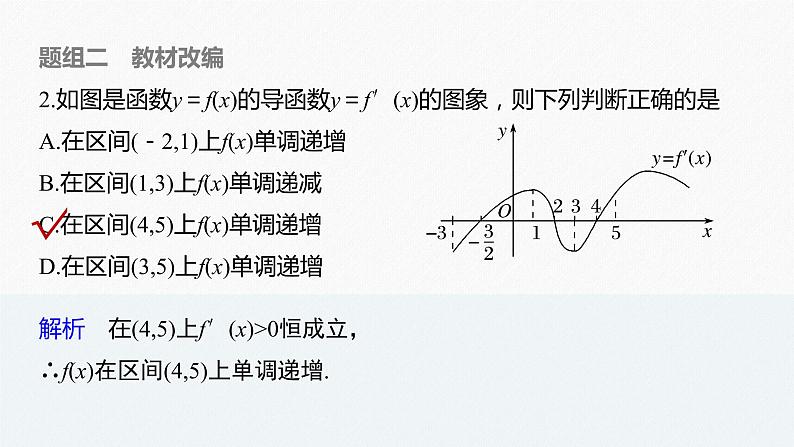
题组二　教材改编2.如图是函数y＝f(x)的导函数y＝f′(x)的图象，则下列判断正确的是A.在区间(－2,1)上f(x)单调递增B.在区间(1,3)上f(x)单调递减C.在区间(4,5)上f(x)单调递增D.在区间(3,5)上f(x)单调递增
解析　在(4,5)上f′(x)>0恒成立，∴f(x)在区间(4,5)上单调递增.
3.函数y＝xcs x－sin x在下面哪个区间上单调递增
解析　y′＝－xsin x，经验证，4个选项中只有在(π，2π)内y′>0恒成立，∴y＝xcs x－sin x在(π，2π)上单调递增.
4.函数f(x)＝(x－2)ex的单调递增区间为 　.
解析　f(x)的定义域为R，f′(x)＝(x－1)ex，令f′(x)＝0，得x＝1，当x∈(1，＋∞)时，f′(x)>0；当x∈(－∞，1)时，f′(x)0)在[2，＋∞)上单调递增，则a的取值范围是 .
∵函数在[2，＋∞)上单调递增，∴[2，＋∞)⊆[a，＋∞)，∴a≤2.又a>0，∴00，∴00时，f(x)在(0，a)上单调递减，在(a，＋∞)上单调递增.
(2)g(x)＝(x－a－1)ex－(x－a)2.
解　g(x)的定义域为R，g′(x)＝(x－a)ex－2(x－a)＝(x－a)(ex－2)，令g′(x)＝0，得x＝a或x＝ln 2，①当a>ln 2时，x∈(－∞，ln 2)∪(a，＋∞)时，f′(x)>0，x∈(ln 2，a)时，f′(x)f(0)，
命题点2　根据函数的单调性求参数的值(范围)例3　已知函数f(x)＝ln x－ ax2－2x(a≠0)在[1,4]上单调递减，则a的取值范围是 .
解析　因为f(x)在[1,4]上单调递减，
引申探究本例中，若f(x)在[1,4]上存在单调递减区间，求a的取值范围.
解　因为f(x)在[1,4]上存在单调递减区间，则f′(x)－1，又因为a≠0，所以a的取值范围是(－1,0)∪(0，＋∞).
根据函数单调性求参数的一般思路(1)利用集合间的包含关系处理：y＝f(x)在(a，b)上单调，则区间(a，b)是相应单调区间的子集.(2)f(x)为增(减)函数的充要条件是对任意的x∈(a，b)都有f′(x)≥0(f′(x)≤0)，且在(a，b)内的任一非空子区间上，f′(x)不恒为零，应注意此时式子中的等号不能省略，否则会漏解.(3)函数在某个区间上存在单调区间可转化为不等式有解问题.
跟踪训练2　(1)已知y＝f(x)是定义在R上的函数，且f(2)＝5，对任意的x都有f′(x)< ，则f(x)< x＋4的解集是 .
∴F(x)为R上的减函数，又F(2)＝f(2)－1＝4，
即F(x)2.
(2)(2020·深圳调研)设函数f(x)＝ x2－9ln x在区间[a－1，a＋1]上单调递减，则实数a的取值范围是 .
因为函数f(x)在区间[a－1，a＋1]上单调递减，
　　以抽象函数为背景、题设条件或所求结论中具有“f(x)±g(x)，f(x)g(x)，　 ”等特征式、旨在考查导数运算法则的逆向、变形应用能力的客观题，是近几年高考试卷中的一位“常客”，常以压轴题小题的形式出现，解答这类问题的有效策略是将前述式子的外形结构特征与导数运算法则结合起来，合理构造出相关的可导函数，然后利用该函数的性质解决问题.
一、构造y＝f(x)±g(x)型可导函数例1　设f(x)为R上的奇函数，当x≥0时，f′(x)－cs x