高中数学高考第1节 集合 教案

这是一份高中数学高考第1节 集合 教案，共11页。
[最新考纲] 1．了解集合的含义，体会元素与集合的属于关系；能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题．2．理解集合之间包含与相等的含义，能识别给定集合的子集；在具体情境中，了解全集与空集的含义．3．(1)理解两个集合的并集与交集的含义，会求两个简单集合的并集与交集．(2)理解在给定集合中一个子集的补集的含义，会求给定子集的补集．(3)能使用Venn图表达集合间的基本关系及集合的基本运算．
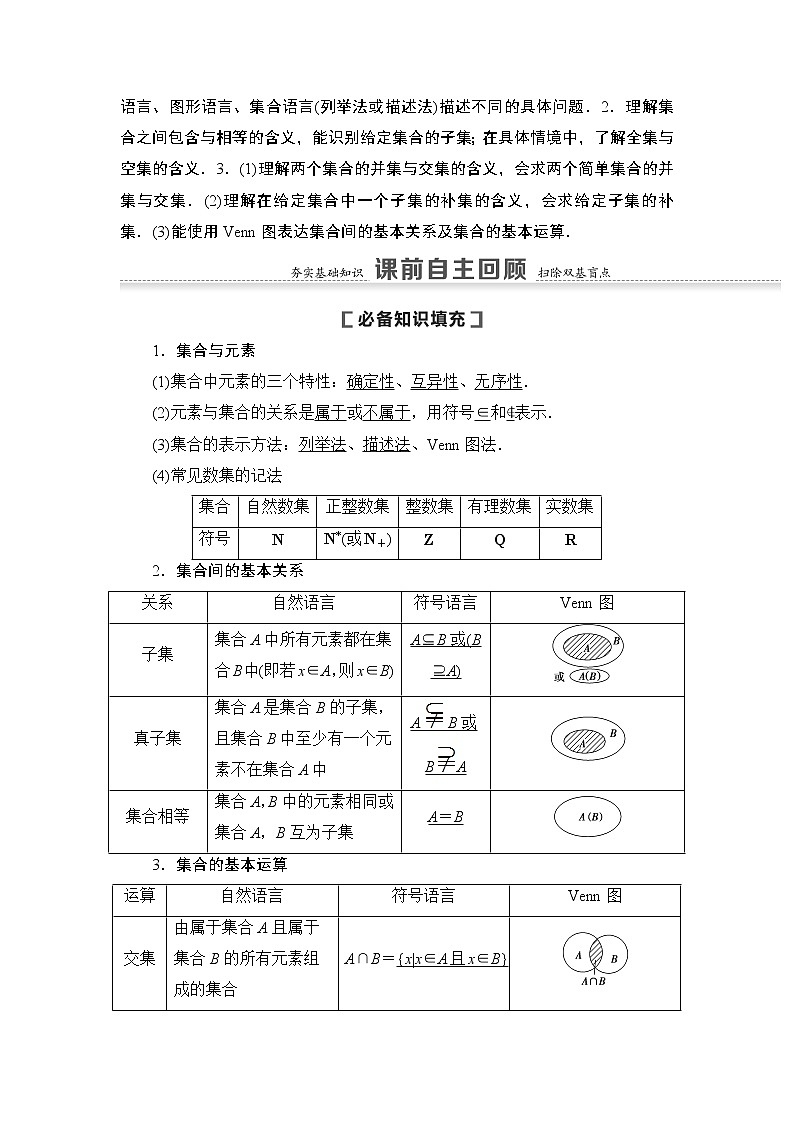
1．集合与元素
(1)集合中元素的三个特性：确定性、互异性、无序性．
(2)元素与集合的关系是属于或不属于，用符号∈和∉表示．
(3)集合的表示方法：列举法、描述法、Venn图法．
(4)常见数集的记法
2．集合间的基本关系
3．集合的基本运算
eq \([常用结论])
1．集合子集的个数
对于有限集合A，其元素个数为n，则集合A的子集个数为2n，真子集个数为2n－1，非空真子集个数为2n－2．
2．集合的运算性质
(1)并集的性质：A∪∅＝A；A∪A＝A；A∪B＝B∪A；A∪B＝A⇔B⊆A．
(2)交集的性质：A∩∅＝∅；A∩A＝A；A∩B＝B∩A；A∩B＝A⇔A⊆B．
(3)补集的性质：A∪(∁UA)＝U；A∩(∁UA)＝∅；∁U(∁UA)＝A；∁U(A∩B)＝(∁UA)∪(∁UB)；∁U(A∪B)＝(∁UA)∩(∁UB)．
一、思考辨析(正确的打“√”，错误的打“×”)
(1)任何一个集合都至少有两个子集．( )
(2){x|y＝x2}＝{y|y＝x2}＝{(x，y)|y＝x2}．( )
(3)若{x2,1}＝{0,1}，则x＝0,1．( )
(4)直线y＝x＋3与y＝－2x＋6的交点组成的集合是{1,4}．( )
[答案] (1)× (2)× (3)× (4)×
二、教材改编
1．若集合A＝{x∈N|x≤2eq \r(2)}，a＝eq \r(2)，则下列结论正确的是( )
A．{a}⊆A B．a⊆A
C．{a}∈A D．a∉A
D [由题意知A＝{0,1,2}，由a＝eq \r(2)，知a∉A．]
2．已知集合M＝{0,1,2,3,4}，N＝{1,3,5}，则集合M∪N的子集的个数为________．
64 [∵M＝{0,1,2,3,4}，N＝{1,3,5}，
∴M∪N＝{0,1,2,3,4,5}，
∴M∪N的子集有26＝64个．]
3．已知U＝{α|0°＜α＜180°}，A＝{x|x是锐角}，B＝{x|x是钝角}，则∁U(A∪B)＝________．
[答案] {x|x是直角}
4．方程组eq \b\lc\{\rc\ (\a\vs4\al\c1(x＋y＝1，,2x－y＝1))的解集为________．
eq \b\lc\{\rc\}(\a\vs4\al\c1(\f(2,3)，\f(1,3))) [由eq \b\lc\{\rc\ (\a\vs4\al\c1(x＋y＝1，,2x－y＝1，))得eq \b\lc\{\rc\ (\a\vs4\al\c1(x＝\f(2,3)，,y＝\f(1,3)，))
故方程组的解集为eq \b\lc\{\rc\}(\a\vs4\al\c1(\f(2,3)，\f(1,3)))．]
5．已知集合A＝{x|－2＜x＜3}，集合B＝{x|x－1＜0}，则A∩B＝________，A∪B＝________．
(－2,1) (－∞，3) [∵A＝{x|－2＜x＜3}，B＝{x|x－1＜0}＝{x|x＜1}，
∴A∩B＝{x|－2＜x＜1}，A∪B＝{x|x＜3}．]
考点1 集合的概念
与集合中的元素有关的问题的求解思路
(1)确定集合的元素是什么，即集合是数集还是点集．
(2)看清元素的限制条件．
(3)根据限制条件求参数的值或确定集合中元素的个数．
1．已知集合A＝{(x，y)|x2＋y2≤3，x∈Z，y∈Z}，则A中元素的个数为( )
A．9 B．8 C．5 D．4
A [由x2＋y2≤3知，－eq \r(3)≤x≤eq \r(3)，－eq \r(3)≤y≤eq \r(3)．又x∈Z，y∈Z，所以x∈{－1,0,1}，y∈{－1,0,1}，所以A中元素的个数为9，故选A．]
2．已知集合A＝{m＋2,2m2＋m}，若3∈A，则m的值为________．
－eq \f(3,2) [由题意得m＋2＝3或2m2＋m＝3，
则m＝1或m＝－eq \f(3,2)．
当m＝1时，m＋2＝3且2m2＋m＝3，根据集合中元素的互异性可知不满足题意；
当m＝－eq \f(3,2)时，m＋2＝eq \f(1,2)，而2m2＋m＝3，符合题意，故m＝－eq \f(3,2)．]
3．若集合A＝{x∈R|ax2－3x＋2＝0}中只有一个元素，则a＝________．
0或eq \f(9,8) [当a＝0时，显然成立；当a≠0时，Δ＝(－3)2－8a＝0，即a＝eq \f(9,8)．]
4．已知a，b∈R，若eq \b\lc\{\rc\}(\a\vs4\al\c1(a，\f(b,a)，1))＝{a2，a＋b,0}，则a2 020＋b2 020＝________．
1 [由已知得a≠0，则eq \f(b,a)＝0，
所以b＝0，于是a2＝1，即a＝1或a＝－1，又根据集合中元素的互异性可知a＝1应舍去，因此a＝－1，故a2 020＋b2 020＝(－1)2 020＋02 020＝1．]
(1)求解此类问题时，要特别注意集合中元素的互异性，如T2，T4．(2)常用分类讨论的思想方法求解集合问题，如T3．
考点2 集合的基本关系
判断两集合关系的方法
(1)列举法：用列举法表示集合，再从元素中寻求关系．
(2)化简集合法：用描述法表示的集合，若代表元素的表达式比较复杂，往往需化简表达式，再寻求两个集合的关系．
(1)(2019·唐山模拟)设集合M＝{x|x2－x＞0}，N＝eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(\f(1,x)＜1))))，则( )
A．MN B．NM
C．M＝N D．M∪N＝R
(2)已知集合A＝{x|x2－3x＋2＝0，x∈R}，B＝{x|0＜x＜5，x∈N}，则满足条件A⊆C⊆B的集合C的个数为( )
A．1 B．2 C．3 D．4
(3)已知集合A＝{x|－2≤x≤5}，B＝{x|m＋1≤x≤2m－1}，若B⊆A，则实数m的取值范围为________．
(1)C (2)D (3)(－∞，3] [(1)集合M＝{x|x2－x＞0}＝{x|x＞1或x＜0}，N＝eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(\f(1,x)＜1))))＝{x|x＞1或x＜0}，所以M＝N．故答案为C．
(2)因为A＝{1,2}，B＝{1,2,3,4}，A⊆C⊆B，则集合C可以为：{1,2}，{1,2,3}，{1,2,4}，{1,2,3,4}共4个．
(3)因为B⊆A，
所以①若B＝∅，则2m－1＜m＋1，此时m＜2．
②若B≠∅，则eq \b\lc\{\rc\ (\a\vs4\al\c1(2m－1≥m＋1，,m＋1≥－2，,2m－1≤5.))解得2≤m≤3．
由①②可得，符合题意的实数m的取值范围为(－∞，3]．]
[母题探究]
1．(变问法)本例(3)中，若BA，求m的取值范围．
[解] 因为BA，
①若B＝∅，成立，此时m＜2．
②若B≠∅，则eq \b\lc\{\rc\ (\a\vs4\al\c1(2m－1≥m＋1，,m＋1≥－2，,2m－1≤5，))且边界点不能同时取得，解得2≤m≤3．
综合①②，m的取值范围为(－∞，3]．
2．(变问法)本例(3)中，若A⊆B，求m的取值范围．
[解] 若A⊆B，则eq \b\lc\{\rc\ (\a\vs4\al\c1(m＋1≤－2，,2m－1≥5，))即eq \b\lc\{\rc\ (\a\vs4\al\c1(m≤－3，,m≥3.))所以m的取值范围为∅．
3．(变条件)若将本例(3)中的集合A改为A＝{x|x＜－2或x＞5}，试求m的取值范围．
[解] 因为B⊆A，
所以①当B＝∅时，2m－1＜m＋1，即m＜2，符合题意．
②当B≠∅时，eq \b\lc\{\rc\ (\a\vs4\al\c1(m＋1≤2m－1，,m＋1＞5))或eq \b\lc\{\rc\ (\a\vs4\al\c1(m＋1≤2m－1，,2m－1＜－2，))
解得eq \b\lc\{\rc\ (\a\vs4\al\c1(m≥2，,m＞4))或eq \b\lc\{\rc\ (\a\vs4\al\c1(m≥2，,m＜－\f(1,2)，))即m＞4．
综上可知，实数m的取值范围为(－∞，2)∪(4，＋∞)．
(1)已知两个集合间的关系求参数时，关键是将条件转化为元素或区间端点间的关系，进而转化为参数所满足的关系，常用数轴、Venn图等来直观解决这类问题．
(2)空集是任何集合的子集，当题目条件中有B⊆A时，应分B＝∅和B≠∅两种情况讨论．
1．设M为非空的数集，M⊆{1,2,3}，且M中至少含有一个奇数元素，则这样的集合M共有( )
A．6个 B．5个 C．4个 D．3个
A [由题意知，M＝{1}，{3}，{1,2}，{1,3}，{2,3}，{1,2,3}，共6个．]
2．若集合A＝{1,2}，B＝{x|x2＋mx＋1＝0，x∈R}，且B⊆A，则实数m的取值范围为________．
[－2,2) [①若B＝∅，则Δ＝m2－4＜0，
解得－2＜m＜2，符合题意；
②若1∈B，则12＋m＋1＝0，
解得m＝－2，此时B＝{1}，符合题意；
③若2∈B，则22＋2m＋1＝0，
解得m＝－eq \f(5,2)，此时B＝eq \b\lc\{\rc\}(\a\vs4\al\c1(2，\f(1,2)))，不合题意．
综上所述，实数m的取值范围为[－2,2)．]
考点3 集合的基本运算
集合运算三步骤
集合的运算
(1)(2019·全国卷Ⅰ)已知集合U＝{1,2,3,4,5,6,7}，A＝{2,3,4,5}，B＝{2,3,6,7}，则B∩∁UA＝( )
A．{1,6} B．{1,7}
C．{6,7} D．{1,6,7}
(2)(2019·全国卷Ⅱ)已知集合A＝{x|x＞－1}，B＝{x|x＜2}，则A∩B＝( )
A．(－1，＋∞) B．(－∞，2)
C．(－1,2) D．∅
(3)(2019·全国卷Ⅲ)已知集合A＝{－1,0,1,2}，B＝{x|x2≤1}，则A∩B＝( )
A．{－1,0,1} B．{0,1}
C．{－1,1} D．{0,1,2}
(1)C (2)C (3)A [(1)由题意知∁UA＝{1,6,7}，又B＝{2,3,6,7}，∴B∩∁UA＝{6,7}，故选C．
(2)∵A＝{x|x＞－1}，B＝{x|x＜2}，∴A∩B＝{x|－1＜x＜2}，即A∩B＝(－1,2)．
故选C．
(3)由题意可知B＝{x|－1≤x≤1}，
又∵A＝{－1,0,1,2}，
∴A∩B＝{－1,0,1}，
故选A．]
[逆向问题]
已知A，B均为集合U＝{1,3,5,7,9}的子集，且A∩B＝{3}，(∁UB)∩A＝{9}，则A＝( )
A．{1,3} B．{3,7,9}
C．{3,5,9} D．{3,9}
D [法一：(直接法)因为A∩B＝{3}，所以3∈A，又(∁UB)∩A＝{9}，所以9∈A．若5∈A，则5∉B(否则5∈A∩B)，从而5∈∁UB，则(∁UB)∩A＝{5,9}，与题中条件矛盾，故5∉A．同理，1∉A,7∉A，故A＝{3,9}．
法二：(Venn图)如图所示．
]
集合运算的常用方法
(1)若集合中的元素是离散的，常用Venn图求解．
(2)若集合中的元素是连续的实数，则用数轴表示，此时要注意端点的情况．
利用集合的运算求参数
(1)已知集合M＝{x|0＜x＜5}，N＝{x|m＜x＜6}，若M∩N＝{x|3＜x＜n}，则m＋n等于( )
A．9 B．8 C．7 D．6
(2)集合A＝{0,2，a}，B＝{1，a2}，若A∪B＝{0,1,2,4,16}，则a的值为( )
A．0 B．1 C．2 D．4
(1)B (2)D [(1)因为M∩N＝{x|0＜x＜5}∩{x|m＜x＜6}＝{x|3＜x＜n}，所以m＝3，n＝5，因此m＋n＝8．故选B．
(2)根据并集的概念，可知{a，a2}＝{4,16}，故只能是a＝4．]
利用集合的运算求参数的值或取值范围的方法
(1)若集合中的元素能一一列举，则一般先用观察法得到不同集合中元素之间的关系，再列方程(组)求解．
(2)与不等式有关的集合，一般利用数轴解决，要注意端点值能否取到．
提醒：在求出参数后，注意结果的验证(满足互异性)．
[教师备选例题]
1．已知集合A＝{(x，y)|x2＋y2≤1，x，y∈Z}，B＝{(x，y)||x|≤2，|y|≤2，x，y∈Z}，定义集合AB＝{(x1＋x2，y1＋y2)|(x1，y1)∈A，(x2，y2)∈B}，则AB中元素的个数为( )
A．77 B．49 C．45 D．30
C [如图，集合A表示如图所示的所有圆点“”，集合B表示如图所示的所有圆点“”＋所有圆点“”，集合AB显然是集合{(x，y)||x|≤3，|y|≤3，x，y∈Z}中除去四个点{(－3，－3)，(－3,3)，(3，－3)，(3,3)}之外的所有整点(即横坐标与纵坐标都为整数的点)，则集合AB表示如图所示的所有圆点“”＋所有圆点“”＋所有圆点“”，共45个．故AB中元素的个数为45．故选C．
]
2．设集合A＝{x|x2＋2x－3＞0}，集合B＝{x|x2－2ax－1≤0，a＞0}，若A∩B中恰含有一个整数，则实数a的取值范围是( )
A．eq \b\lc\(\rc\)(\a\vs4\al\c1(0，\f(3,4))) B．eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(3,4)，\f(4,3)))
C．eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(3,4)，＋∞)) D．(1，＋∞)
B [A＝{x|x2＋2x－3＞0}＝{x|x＞1或x＜－3}，设函数f(x)＝x2－2ax－1，因为函数f(x)＝x2－2ax－1图象的对称轴为直线x＝a(a＞0)，f(0)＝－1＜0，根据对称性可知若A∩B中恰有一个整数，则这个整数为2，所以有eq \b\lc\{\rc\ (\a\vs4\al\c1(f2≤0，,f3＞0，))即eq \b\lc\{\rc\ (\a\vs4\al\c1(4－4a－1≤0，,9－6a－1＞0，))所以eq \b\lc\{\rc\ (\a\vs4\al\c1(a≥\f(3,4)，,a＜\f(4,3)，))
即eq \f(3,4)≤a＜eq \f(4,3)．故选B．]
1．(2019·许昌、洛阳三模)已知集合A＝{x|y＝eq \r(－x2＋1)}，B＝(0,1)，则A∩B＝( )
A．(0,1) B．(0,1]
C．(－1,1) D．[－1,1]
A [由题意得A＝[－1,1]，又B＝(0,1)，∴A∩B＝(0,1)．故选A．]
2．(2019·合肥巢湖一模)已知集合A＝{x|x＜3}，B＝{x|x＞a}，若A∩B≠∅，则实数a的取值范围为( )
A．[3，＋∞) B．(3，＋∞)
C．(－∞，3) D．(－∞，3]
C [因为A∩B≠∅，所以结合数轴(图略)可知实数a的取值范围是a＜3，故选C．]
3．(2019·安徽宣城八校联考期末)如图，设全集U＝N，集合A＝{1,3,5,7,8}，B＝{1,2,3,4,5}，则图中阴影部分表示的集合为( )
A．{2,4} B．{7,8}
C．{1,3,5} D．{1,2,3,4,5}
A [由题图可知阴影部分表示的集合为(∁UA)∩B，因为集合A＝{1,3,5,7,8}，B＝{1,2,3,4,5}，U＝N，所以(∁UA)∩B＝{2,4}．故选A．]
4．已知A＝{1,2,3,4}，B＝{a＋1,2a}．若A∩B＝{4}，则a＝________．
3 [因为A∩B＝{4}，所以a＋1＝4或2a＝4．若a＋1＝4，则a＝3，此时B＝{4,6}，符合题意；若2a＝4，则a＝2，此时B＝{3,4}，不符合题意．综上，a＝3．]
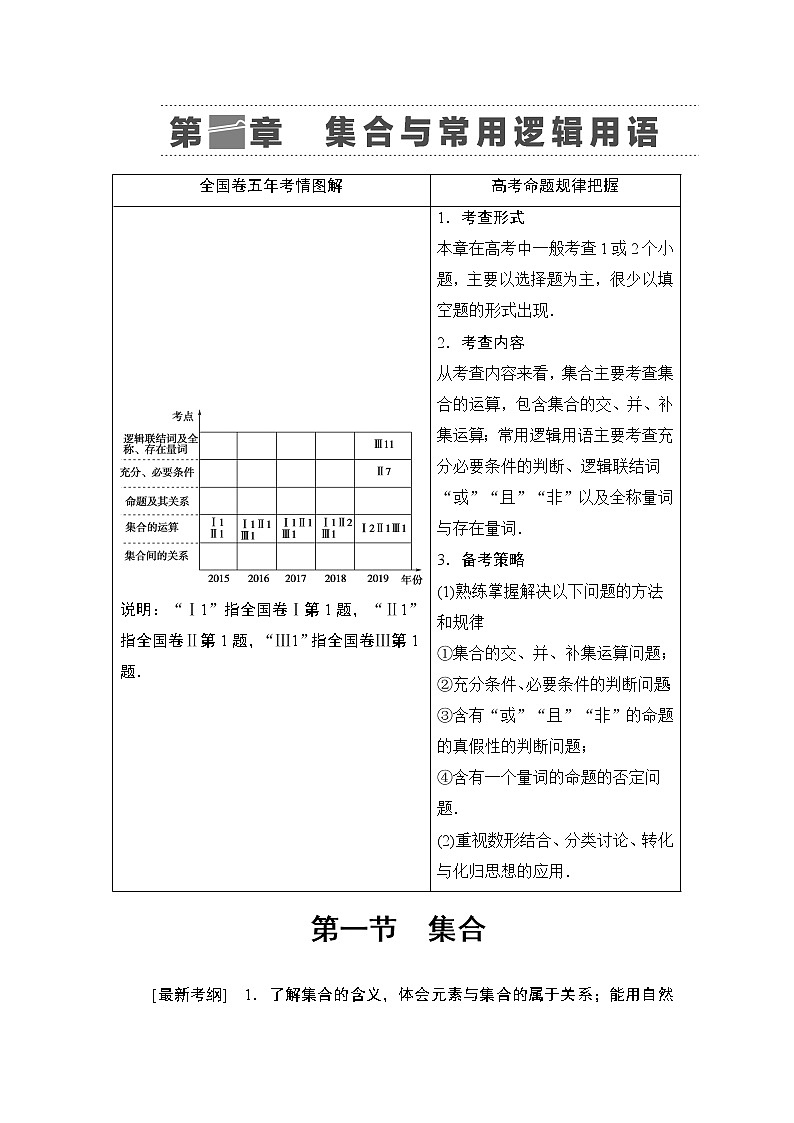
全国卷五年考情图解
高考命题规律把握
说明：“Ⅰ1”指全国卷Ⅰ第1题，“Ⅱ1”指全国卷Ⅱ第1题，“Ⅲ1”指全国卷Ⅲ第1题．
1．考查形式
本章在高考中一般考查1或2个小题，主要以选择题为主，很少以填空题的形式出现．
2．考查内容
从考查内容来看，集合主要考查集合的运算，包含集合的交、并、补集运算；常用逻辑用语主要考查充分必要条件的判断、逻辑联结词“或”“且”“非”以及全称量词与存在量词．
3．备考策略
(1)熟练掌握解决以下问题的方法和规律
①集合的交、并、补集运算问题；
②充分条件、必要条件的判断问题；
③含有“或”“且”“非”的命题的真假性的判断问题；
④含有一个量词的命题的否定问题．
(2)重视数形结合、分类讨论、转化与化归思想的应用．
集合
自然数集
正整数集
整数集
有理数集
实数集
符号
N
N*(或N＋)
Z
Q
R
关系
自然语言
符号语言
Venn图
子集
集合A中所有元素都在集合B中(即若x∈A，则x∈B)
A⊆B或(B⊇A)
真子集
集合A是集合B的子集，且集合B中至少有一个元素不在集合A中
AB或BA
集合相等
集合A，B中的元素相同或集合A，B互为子集
A＝B
运算
自然语言
符号语言
Venn图
交集
由属于集合A且属于集合B的所有元素组成的集合
A∩B＝{x|x∈A且x∈B}
并集
由所有属于集合A或属于集合B的元素组成的集合
A∪B＝{x|x∈A或x∈B}
补集
由全集U中不属于集合A的所有元素组成的集合
∁UA＝{x|x∈U且x∉A}