高中数学高考第4讲　第1课时　三角函数的图象与性质(一)

这是一份高中数学高考第4讲　第1课时　三角函数的图象与性质(一)，共16页。试卷主要包含了知识梳理，教材衍化等内容，欢迎下载使用。

一、知识梳理
1．用五点法作正弦函数和余弦函数的简图
(1)正弦函数y＝sin x，x∈[0，2π]的图象中，五个关键点是：(0，0)，eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，1))，(π，0)，eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)π，－1))，(2π，0)．
(2)余弦函数y＝cs x，x∈[0，2π]的图象中，五个关键点是：(0，1)，eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)，0))，(π，－1)，eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,2)，0))，(2π，1)．
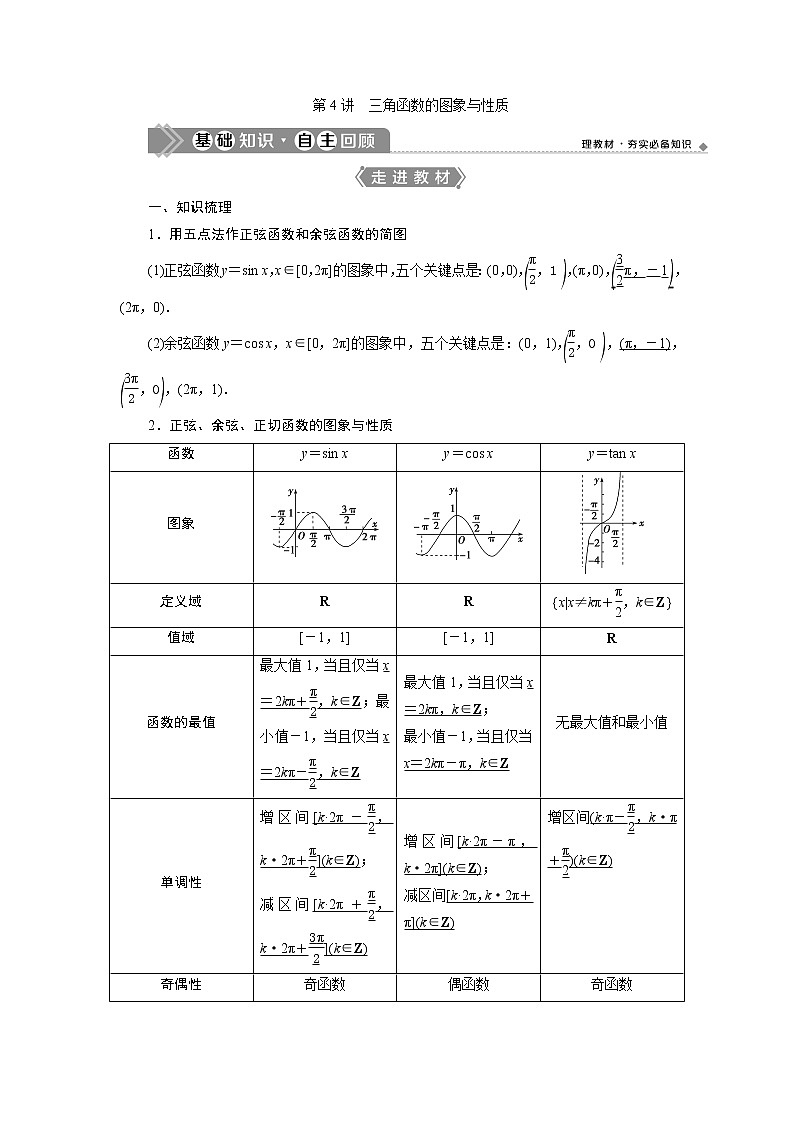
2．正弦、余弦、正切函数的图象与性质
3.周期函数的定义
对于函数f(x)，如果存在一个非零常数T，使得当x取定义域内的每一个值时，都有f(x＋T)＝f(x)，那么函数f(x)就叫做周期函数，非零常数T叫做这个函数的周期；函数y＝Asin(ωx＋φ)和y＝Acs(ωx＋φ)的周期均为T＝eq \f(2π,|ω|)；函数y＝Atan(ωx＋φ)的周期为T＝eq \f(π,|ω|).
常用结论
1．函数y＝sin x与y＝cs x的对称轴分别是经过其图象的最高点或最低点且垂直于x轴的直线，如y＝cs x的对称轴为x＝kπ(k∈Z)，而不是x＝2kπ(k∈Z)．
2．对于y＝tan x不能认为其在定义域上为增函数，而是在每个区间eq \b\lc\(\rc\)(\a\vs4\al\c1(kπ－\f(π,2)，kπ＋\f(π,2)))(k∈Z)内为增函数．
二、教材衍化
1．若函数y＝2sin 2x－1的最小正周期为T，最大值为A，则( )
A．T＝π，A＝1 B．T＝2π，A＝1
C．T＝π，A＝2 D．T＝2π，A＝2
答案：A
2．函数y＝tan 2x的定义域是( )
A．eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|(\a\vs4\al\c1(x≠kx＋\f(π,4)，k∈Z)))) B．eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|(\a\vs4\al\c1(x≠\f(kπ,2)＋\f(π,8)，k∈Z))))
C．eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|(\a\vs4\al\c1(x≠kπ＋\f(π,8)，k∈Z)))) D．eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|(\a\vs4\al\c1(x≠\f(kπ,2)＋\f(π,4)，k∈Z))))
答案：D
3．函数y＝3－2cseq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,4)))的最大值为________，此时x＝________．
答案：5 eq \f(3π,4)＋2kπ(k∈Z)
一、思考辨析
判断正误(正确的打“√”，错误的打“×”)
(1)y＝cs x在第一、二象限内是减函数．( )
(2)若y＝ksin x＋1，x∈R，则y的最大值是k＋1.( )
(3)若非零实数T是函数f(x)的周期，则kT(k是非零整数)也是函数f(x)的周期．( )
(4)函数y＝sin x图象的对称轴方程为x＝2kπ＋eq \f(π,2)(k∈Z)．( )
(5)函数y＝tan x在整个定义域上是增函数．( )
答案：(1)× (2)× (3)√ (4)× (5)×
二、易错纠偏
常见误区eq \b\lc\|(\a\vs4\al\c1( ))(1)忽视y＝Asin x(或y＝Acs x)中A对函数单调性的影响；
(2)忽视正、余弦函数的有界性；
(3)不注意正切函数的定义域．
1．函数y＝1－2cs x的单调递减区间是________．
答案：[2kπ－π，2kπ](k∈Z)
2．函数f(x)＝sin2x＋eq \r(3)cs x－eq \f(3,4)eq \b\lc\(\rc\)(\a\vs4\al\c1(x∈\b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,2)))))的最大值是________．
解析：f(x)＝sin2x＋eq \r(3)cs x－eq \f(3,4)＝1－cs2x＋eq \r(3)cs x－eq \f(3,4)＝－eq \b\lc\(\rc\)(\a\vs4\al\c1(cs x－\f(\r(3),2)))eq \s\up12(2)＋1，cs x∈[0，1]，当cs x＝eq \f(\r(3),2)时，f(x)取得最大值1.
答案：1
3．函数y＝cs xtan x的值域是________．
解析：y＝cs xtan x＝sin x
又cs x≠0，
所以sin x≠±1，
所以y＝sin x∈(－1，1)．
答案：(－1，1)
第1课时 三角函数的图象与性质(一)
考点一 三角函数的定义域(基础型)
eq \a\vs4\al(复习,指导)eq \b\lc\|(\a\vs4\al\c1( ))求三角函数定义域实际上是构造简单的三角不等式(组)，常借助三角函数线或三角函数图象来求解．
1．函数f(x)＝－2taneq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,6)))的定义域是( )
A．eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|(\a\vs4\al\c1(x≠\f(π,6)))))
B．eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|(\a\vs4\al\c1(x≠－\f(π,12)))))
C．eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|(\a\vs4\al\c1(x≠kπ＋\f(π,6)))（k∈Z）))
D．eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|(\a\vs4\al\c1(x≠\f(kπ,2)＋\f(π,6)))（k∈Z）))
解析：选D．由2x＋eq \f(π,6)≠kπ＋eq \f(π,2)，得x≠eq \f(kπ,2)＋eq \f(π,6)(k∈Z)．
2．函数y＝lg sin x＋eq \r(cs x －\f(1,2))的定义域为________．
解析：要使函数有意义，则有eq \b\lc\{(\a\vs4\al\c1(sin x>0，,cs x－\f(1,2)≥0，))
即eq \b\lc\{(\a\vs4\al\c1(sin x>0，,cs x≥\f(1,2)，))
解得eq \b\lc\{(\a\vs4\al\c1(2kπ