高中数学高考第5节 函数y＝Asin(ωx＋φ)的图象及三角函数模型的简单应用 教案

这是一份高中数学高考第5节 函数y＝Asin(ωx＋φ)的图象及三角函数模型的简单应用 教案，共14页。

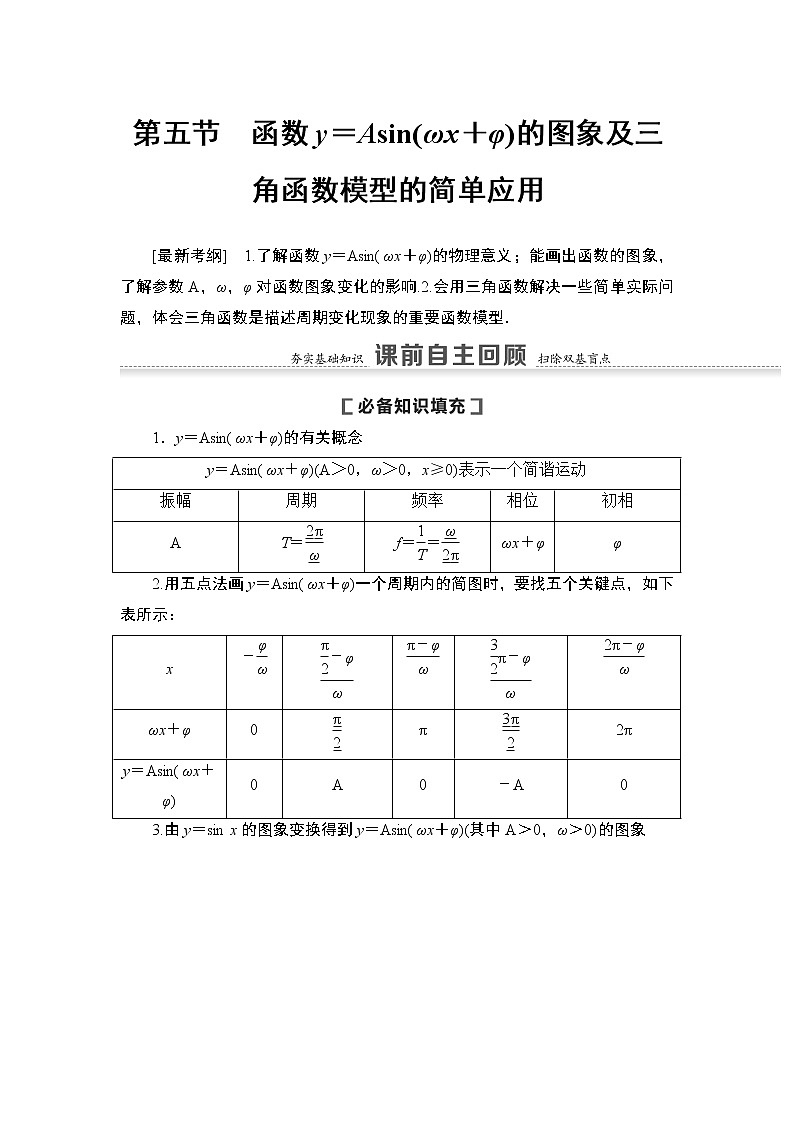
1．y＝Asin(ωx＋φ)的有关概念
2.用五点法画y＝Asin(ωx＋φ)一个周期内的简图时，要找五个关键点，如下表所示：
3.由y＝sin x的图象变换得到y＝Asin(ωx＋φ)(其中A＞0，ω＞0)的图象
eq \([常用结论])
1．函数y＝Asin(ωx＋φ)＋k图象平移的规律：“左加右减，上加下减”．
2．由y＝sin ωx到y＝sin(ωx＋φ) 0)的变换：向左平移eq \f(φ,ω)个单位长度而非φ个单位长度．
一、思考辨析(正确的打“√”，错误的打“×”)
(1)利用图象变换作图时“先平移，后伸缩”与“先伸缩，后平移”中平移的单位长度一致．( )
(2)将y＝3sin 2x的图象左移eq \f(π,4)个单位后所得图象的解析式是y＝3sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,4))).( )
(3)y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,4)))的图象是由y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,4)))的图象向右平移eq \f(π,2)个单位得到的．( )
(4)函数y＝Acs(ωx＋φ)的最小正周期为T，那么函数图象的两个相邻对称中心之间的距离为eq \f(T,2).( )
[答案] (1)× (2)× (3)√ (4)√
二、教材改编
1．y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,2)x－\f(π,3)))的振幅、频率和初相分别为( )
A．2,4π，eq \f(π,3) B．2，eq \f(1,4π)，eq \f(π,3)
C．2，eq \f(1,4π)，－eq \f(π,3) D．2,4π，－eq \f(π,3)
C [由题意知A＝2，f＝eq \f(1,T)＝eq \f(ω,2π)＝eq \f(1,4π)，初相为－eq \f(π,3).]
2．为了得到函数y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,3)))的图象，可以将函数y＝2sin 2x的图象( )
A．向右平移eq \f(π,6)个单位长度
B．向右平移eq \f(π,3)个单位长度
C．向左平移eq \f(π,6)个单位长度
D．向左平移eq \f(π,3)个单位长度
A [y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,3)))＝2sin 2eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,6))).]
3．如图，某地一天从6～14时的温度变化曲线近似满足函数y＝Asin(ωx＋φ)＋b，则这段曲线的函数解析式为________．
y＝10sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,8)x＋\f(3π,4)))＋20，x∈[6,14] [从图中可以看出，从6～14时的是函数y＝Asin(ωx＋φ)＋b的半个周期
所以A＝eq \f(1,2)×(30－10)＝10，b＝eq \f(1,2)×(30＋10)＝20，
又eq \f(1,2)×eq \f(2π,ω)＝14－6，所以ω＝eq \f(π,8).
又eq \f(π,8)×10＋φ＝2π＋2kπ，k∈Z，取φ＝eq \f(3π,4)，
所以y＝10sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,8)x＋\f(3π,4)))＋20，x∈[6,14]．]
4．某地农业监测部门统计发现：该地区近几年的生猪收购价格每四个月会重复出现．下表是今年前四个月的统计情况：
选用一个函数来近似描述收购价格(元/斤)与相应月份之间的函数关系为________．
y＝6－cseq \f(π,2)x [设y＝Asin(ωx＋φ)＋B(A＞0，ω＞0)，由题意得A＝1，B＝6，T＝4，因为T＝eq \f(2π,ω)，所以ω＝eq \f(π,2)，所以y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)x＋φ))＋6.因为当x＝1时，y＝6，所以6＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)＋φ))＋6，结合表中数据得eq \f(π,2)＋φ＝2kπ，k∈Z，可取φ＝－eq \f(π,2)，所以y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,2)x－\f(π,2)))＋6＝6－cs eq \f(π,2)x.]
考点1 函数y＝Asin(ωx＋φ)的图象及变换
(1)y＝Asin(ωx＋φ)的图象可用“五点法”作简图得到，可通过变量代换z＝ωx＋φ计算五点坐标．
(2)由函数y＝sin x的图象通过变换得到y＝Asin(ωx＋φ)图象有两条途径：“先平移后伸缩”与“先伸缩后平移”．
已知函数y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3))).
(1)用“五点法”作出它在一个周期内的图象；
(2)[一题多解]说明y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))的图象可由y＝sin x的图象经过怎样的变换而得到．
[解] (1)描点画出图象，如图所示：
(2)法一：把y＝sin x的图象上所有的点向左平移eq \f(π,3)个单位长度，得到y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,3)))的图象；
再把y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,3)))的图象上所有点的横坐标缩短到原来的eq \f(1,2)倍(纵坐标不变)，得到y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))的图象；
最后把y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))上所有点的纵坐标伸长到原来的2倍(横坐标不变)，即可得到y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))的图象．
法二：将y＝sin x的图象上所有点的横坐标缩短为原来的eq \f(1,2)倍(纵坐标不变)，得到y＝sin 2x的图象；
再将y＝sin 2x的图象向左平移eq \f(π,6)个单位长度，得到y＝sineq \b\lc\[\rc\](\a\vs4\al\c1(2\b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,6)))))＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))的图象；
再将y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))的图象上所有点的纵坐标伸长为原来的2倍(横坐标不变)，即得到y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))的图象．
三角函数图象变换中的三个注意点
(1)变换前后，函数的名称要一致，若不一致，应先利用诱导公式转化为同名函数；
(2)要弄清变换的方向，即变换的是哪个函数的图象，得到的是哪个函数的图象，切不可弄错方向；
(3)要弄准变换量的大小，特别是平移变换中，函数y＝Asin x到y＝Asin(x＋φ)的变换量是|φ|个单位，而函数y＝Asin ωx到y＝Asin(ωx＋φ)时，变换量是eq \b\lc\|\rc\|(\a\vs4\al\c1(\f(φ,ω)))个单位．
1.要得到函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(5x－\f(π,4)))的图象，只需将函数y＝cs 5x的图象( )
A．向左平移eq \f(3π,20)个单位
B．向右平移eq \f(3π,20)个单位
C．向左平移eq \f(3π,4)个单位
D．向右平移eq \f(3π,4)个单位
B [函数y＝cs 5x＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(5x＋\f(π,2)))＝sin 5eq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,10)))，
y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(5x－\f(π,4)))＝sin 5eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(π,20)))，设平移φ个单位，
则eq \f(π,10)＋φ＝－eq \f(π,20)，
解得φ＝－eq \f(3π,20)，故把函数y＝cs 5x的图象向右平移eq \f(3π,20)个单位，可得函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(5x－\f(π,4)))的图象．]
2．若把函数y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(ωx－\f(π,6)))的图象向左平移eq \f(π,3)个单位长度，所得到的图象与函数y＝cs ωx的图象重合，则ω的一个可能取值是( )
A．2 B.eq \f(3,2)
C.eq \f(2,3) D.eq \f(1,2)
A [y＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(ωx＋\f(ω,3)π－\f(π,6)))和函数y＝cs ωx的图象重合，可得eq \f(ω,3)π－eq \f(π,6)＝eq \f(π,2)＋2kπ，k∈Z，则ω＝6k＋2，k∈Z.
∴2是ω的一个可能值．]
3．将函数f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(4x＋\f(π,3)))的图象向左平移φ(φ＞0)个单位后，得到的图象关于直线x＝eq \f(π,12)对称，则φ的最小值为________．
eq \f(5,24)π [把函数f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(4x＋\f(π,3)))的图象向左平移φ(φ＞0)个单位后，
可得y＝sineq \b\lc\[\rc\](\a\vs4\al\c1(4x＋φ＋\f(π,3)))＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(4x＋4φ＋\f(π,3)))的图象，
∵所得图象关于直线x＝eq \f(π,12)对称，∴4×eq \f(π,12)＋4φ＋eq \f(π,3)＝eq \f(π,2)＋kπ(k∈Z)，∴φ＝eq \f(kπ,4)－eq \f(π,24)(k∈Z)，
∵φ＞0，∴φmin＝eq \f(5π,24).]
考点2 由图象确定y＝Asin(ωx＋φ)的解析式
确定y＝Asin(ωx＋φ)＋B(A＞0，ω＞0)的解析式的步骤
(1)求A，B，确定函数的最大值M和最小值m，则A＝eq \f(M－m,2)，B＝eq \f(M＋m,2).
(2)求ω，确定函数的周期T，则ω＝eq \f(2π,T).
(3)求φ，常用方法有：
①代入法：把图象上的一个已知点代入(此时要注意该点在上升区间上还是在下降区间上)或把图象的最高点或最低点代入．
②五点法：确定φ值时，往往以寻找“五点法”中的特殊点作为突破口．具体如下：“第一点”(即图象上升时与x轴的交点)为ωx＋φ＝0；“第二点”(即图象的“峰点”)为ωx＋φ＝eq \f(π,2)；“第三点”(即图象下降时与x轴的交点)为ωx＋φ＝π；“第四点”(即图象的“谷点”)为ωx＋φ＝eq \f(3π,2)；“第五点”(即图象上升时与x轴的交点)为ωx＋φ＝2π.
(1)函数f(x)＝Asin(ωx＋φ)的部分图象如图所示，则f(x)＝________.
(2)(2019·重庆六校联考)函数f(x)＝Asin(ωx＋φ)eq \b\lc\(\rc\)(\a\vs4\al\c1(A，ω，φ是常数，A＞0，ω＞0，0＜φ＜\f(π,2)))的部分图象如图所示，则feq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,3)))＝________.
(1)2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6))) (2)－eq \f(\r(6),2) [(1)由题图可知，A＝2，T＝2eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,3)－\b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,6)))))＝π，所以ω＝2，由五点作图法可知2×eq \f(π,3)＋φ＝eq \f(π,2)，所以φ＝－eq \f(π,6)，所以函数的解析式为y＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x－\f(π,6))).
(2)由函数的图象可得A＝eq \r(2)，eq \f(1,4)×eq \f(2π,ω)＝eq \f(7π,12)－eq \f(π,3)，可得ω＝2，则2×eq \f(π,3)＋φ＝π＋2kπ(k∈Z)，又0＜φ＜eq \f(π,2)，所以φ＝eq \f(π,3)，故f(x)＝eq \r(2)sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3)))，所以feq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,3)))＝－eq \f(\r(6),2).]
一般情况下，ω的值是唯一确定的，但φ的值是不确定的，它有无数个，如果求出的φ的值不在指定范围内，可以通过加减eq \f(2π,ω)的整数倍达到目的．
1.(2019·开封模拟)如果存在正整数ω和实数φ使得函数f(x)＝sin2(ωx＋φ)的图象如图所示(图象经过点(1,0))，那么ω的值为( )
A．1 B．2
C．3 D．4
B [因为f(x)＝sin2(ωx＋φ)＝eq \f(1,2)－eq \f(1,2)cs 2(ωx＋φ)，所以函数f(x)的最小正周期T＝eq \f(2π,2ω)＝eq \f(π,ω)，由题图知eq \f(T,2)＜1，且eq \f(3T,4)＞1，即eq \f(4,3)＜T＜2，又ω为正整数，所以ω的值为2，故选B.]
2.(2019·合肥模拟)函数f(x)＝Asin(ωx＋φ)eq \b\lc\(\rc\)(\a\vs4\al\c1(A＞0，|φ|＜\f(π,2)))的图象如图所示，则下列说法正确的是( )
A．在区间eq \b\lc\[\rc\](\a\vs4\al\c1(\f(7π,6)，\f(13π,6)))上单调递减
B．在区间eq \b\lc\[\rc\](\a\vs4\al\c1(\f(7π,12)，\f(13π,12)))上单调递增
C．在区间eq \b\lc\[\rc\](\a\vs4\al\c1(\f(7π,12)，\f(13π,12)))上单调递减
D．在区间eq \b\lc\[\rc\](\a\vs4\al\c1(\f(7π,6)，\f(13π,6)))上单调递增
B [由题意得，A＝2，T＝4×eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,3)－\f(π,12)))＝π，故ω＝eq \f(2π,π)＝2.当x＝eq \f(π,12)时取得最大值2，所以2＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2×\f(π,12)＋φ))，且|φ|＜eq \f(π,2)，所以φ＝eq \f(π,3)，所以函数的解析式为f(x)＝2sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3))).当x∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(7π,12)，\f(13π,12)))时，2x＋eq \f(π,3)∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(3π,2)，\f(5π,2)))，又由正弦函数y＝sin x的图象与性质可知，函数y＝sin x在eq \b\lc\[\rc\](\a\vs4\al\c1(\f(3π,2)，\f(5π,2)))上单调递增，故函数f(x)在eq \b\lc\[\rc\](\a\vs4\al\c1(\f(7π,12)，\f(13π,12)))上单调递增．当x∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(7π,6)，\f(13π,6)))时，2x＋eq \f(π,3)∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(8π,3)，\f(14π,3)))，由函数y＝sin x的图象与性质知此区间上不单调，故选B.]
3.已知函数f(x)＝sin(πx＋θ)eq \b\lc\(\rc\)(\a\vs4\al\c1(|θ|＜\f(π,2)))的部分图象如图所示，且f(0)＝－eq \f(1,2)，则图中m的值为________．
eq \f(4,3) [因为f(0)＝sin θ＝－eq \f(1,2)，且|θ|＜eq \f(π,2)，所以θ＝－eq \f(π,6)，所以f(x)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(πx－\f(π,6)))，所以f(m)＝sineq \b\lc\(\rc\)(\a\vs4\al\c1(mπ－\f(π,6)))＝－eq \f(1,2)，所以mπ－eq \f(π,6)＝2kπ＋eq \f(7π,6)，k∈Z，所以m＝2k＋eq \f(4,3)，k∈Z.又周期T＝2，所以0＜m＜2，所以m＝eq \f(4,3).]
考点3 三角函数图象与性质的综合应用
已知函数f(x)＝eq \r(3)sineq \b\lc\(\rc\)(\a\vs4\al\c1(2ωx＋\f(π,3)))(ω＞0)的图象与x轴相邻两个交点的距离为eq \f(π,2).
(1)求函数f(x)的解析式；
(2)若将f(x)的图象向左平移m(m＞0)个单位长度得到函数g(x)的图象恰好经过点eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,3)，0))，求当m取得最小值时，g(x)在eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,6)，\f(7π,12)))上的单调递增区间．
[解] (1)函数f(x)的图象与x轴相邻两个交点的距离为eq \f(π,2)，
得函数f(x)的最小正周期为T＝2×eq \f(π,2)＝eq \f(2π,2ω)，得ω＝1，
故函数f(x)的解析式为f(x)＝eq \r(3)sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(π,3))).
(2)将f(x)的图象向左平移m(m＞0)个单位长度得到函数g(x)＝eq \r(3)sineq \b\lc\[\rc\](\a\vs4\al\c1(2x＋m＋\f(π,3)))＝eq \r(3)sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋2m＋\f(π,3)))的图象，根据g(x)的图象恰好经过点eq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(π,3)，0))，
可得eq \r(3)sineq \b\lc\(\rc\)(\a\vs4\al\c1(－\f(2π,3)＋2m＋\f(π,3)))＝0，即sineq \b\lc\(\rc\)(\a\vs4\al\c1(2m－\f(π,3)))＝0，
所以2m－eq \f(π,3)＝kπ(k∈Z)，m＝eq \f(kπ,2)＋eq \f(π,6)(k∈Z)，
因为m＞0，
所以当k＝0时，m取得最小值，且最小值为eq \f(π,6).
此时，g(x)＝eq \r(3)sineq \b\lc\(\rc\)(\a\vs4\al\c1(2x＋\f(2π,3))).
因为x∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,6)，\f(7π,12)))，所以2x＋eq \f(2π,3)∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,3)，\f(11π,6))).
当2x＋eq \f(2π,3)∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,3)，\f(π,2)))，即x∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,6)，－\f(π,12)))时，g(x)单调递增，
当2x＋eq \f(2π,3)∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(3π,2)，\f(11π,6)))，即x∈eq \b\lc\[\rc\](\a\vs4\al\c1(\f(5π,12)，\f(7π,12)))时，g(x)单调递增．
综上，g(x)在区间eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,6)，\f(7π,12)))上的单调递增区间是eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,6)，－\f(π,12)))和eq \b\lc\[\rc\](\a\vs4\al\c1(\f(5π,12)，\f(7π,12))).
研究y＝Asin(ωx＋φ)的性质时可将ωx＋φ视为一个整体，利用换元法和数形结合思想进行解题．
1.(2019·全国卷Ⅱ)若x1＝eq \f(π,4)，x2＝eq \f(3π,4)是函数f(x)＝sin ωx(ω＞0)两个相邻的极值点，则ω＝( )
A．2 B.eq \f(3,2) C．1 D.eq \f(1,2)
A [由题意及函数y＝sin ωx的图象与性质可知，
eq \f(1,2)T＝eq \f(3π,4)－eq \f(π,4)，∴T＝π，∴eq \f(2π,ω)＝π，∴ω＝2.
故选A.]
2．(2019·天津高考)已知函数f(x)＝Asin(ωx＋φ)(A＞0，ω＞0，|φ|＜π)是奇函数，将y＝f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)，所得图象对应的函数为g(x)．若g(x)的最小正周期为2π，且geq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)))＝eq \r(2)，则feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,8)))＝( )
A．－2 B．－eq \r(2)
C.eq \r(2) D．2
C [∵f(x)＝Asin(ωx＋φ)为奇函数， ∴φ＝kπ，k∈Z，又|φ|＜π，∴φ＝0，∴f(x)＝Asin ωx，则g(x)＝Asineq \b\lc\(\rc\)(\a\vs4\al\c1(\f(ω,2)x)).由g(x)的最小正周期T＝2π，得eq \f(ω,2)＝eq \f(2π,T)＝1，∴ω＝2.又geq \b\lc\(\rc\)(\a\vs4\al\c1(\f(π,4)))＝Asin eq \f(π,4)＝eq \f(\r(2),2)A＝eq \r(2)，∴A＝2，
∴f(x)＝2sin 2x，∴feq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3π,8)))＝2sin eq \f(3π,4)＝eq \r(2)，故选C.]
数学运算是解决数学问题的基本手段，通过运算可促进学生思维的发展；而逻辑推理是得到数学结论、构建数学体系的重要方式．运算和推理贯穿于探究数学问题的始终，可交替使用，相辅相成．
【例1】 为了使函数y＝sin ωx(ω＞0)在区间[0,1]上至少出现50次最大值，则ω的最小值为( )
A．98π B.eq \f(197,2)π
C.eq \f(199,2)π D．100π
B [由题意，至少出现50次最大值即至少需用49eq \f(1,4)个周期，所以eq \f(197,4)T＝eq \f(197,4)·eq \f(2π,ω)≤1，所以ω≥eq \f(197,2)π.]
[评析] 解决此类问题的关键在于结合条件弄清周期T＝eq \f(2π,ω)与所给区间的关系，从而建立不等关系．
【例2】 [一题多解]若f(x)＝2sin ωx(ω＞0)在区间eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)，\f(2π,3)))上是增函数，则ω的取值范围是________．
eq \b\lc\(\rc\](\a\vs4\al\c1(0，\f(3,4))) [法一：因为x∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)，\f(2π,3)))(ω＞0)，
所以ωx∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(ωπ,2)，\f(2πω,3)))，
因为f(x)＝2sin ωx在eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)，\f(2π,3)))上是增函数，
所以eq \b\lc\{\rc\ (\a\vs4\al\c1(－\f(π,2)ω≥－\f(π,2)，,\f(2π,3)ω≤\f(π,2)，,ω＞0，))
故0＜ω≤eq \f(3,4).
法二：画出函数f(x)＝2sin ωx(ω＞0)的图象如图所示．
要使f(x)在eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)，\f(2π,3)))上是增函数，需eq \b\lc\{\rc\ (\a\vs4\al\c1(－\f(π,2ω)≤－\f(π,2)，,\f(2π,3)≤\f(π,2ω)))(ω＞0)，
即0＜ω≤eq \f(3,4).
法三：由－eq \f(π,2)＋2kπ≤ωx≤eq \f(π,2)＋2kπ(k∈Z)得
－eq \f(π,2ω)＋eq \f(2kπ,ω)≤x≤eq \f(π,2ω)＋eq \f(2kπ,ω)(k∈Z)，
故f(x)的单调递增区间是eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2ω)＋\f(2kπ,ω)，\f(π,2ω)＋\f(2kπ,ω)))(k∈Z)，
由题意eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)，\f(2π,3)))⊆eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2ω)＋\f(2kπ,ω)，\f(π,2ω)＋\f(2kπ,ω)))(k∈Z，ω＞0)，
从而有eq \b\lc\{\rc\ (\a\vs4\al\c1(－\f(π,2ω)≤－\f(π,2)，,\f(π,2ω)≥\f(2π,3)，))即0＜ω≤eq \f(3,4).]
[评析] 根据正弦函数的单调递增区间，确定函数f(x)的单调递增区间，根据函数f(x)＝2sin ωx(ω＞0)在区间eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,2)，\f(2π,3)))上单调递增，建立不等式，即可求ω的取值范围．
【例3】 (1)已知f(x)＝sin ωx－cs ωxeq \b\lc\(\rc\)(\a\vs4\al\c1(ω＞\f(2,3)))，若函数f(x)图象的任何一条对称轴与x轴交点的横坐标都不属于区间(π，2π)，则ω的取值范围是________．(结果用区间表示)
(2)已知函数f(x)＝2sin ωx在区间eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,3)，\f(π,4)))上的最小值为－2，则ω的取值范围是________．
(1)eq \b\lc\[\rc\](\a\vs4\al\c1(\f(3,4)，\f(7,8))) (2) [(1)f(x)＝sin ωx－cs ωx＝eq \r(2)sineq \b\lc\(\rc\)(\a\vs4\al\c1(ωx－\f(π,4)))，
令ωx－eq \f(π,4)＝eq \f(π,2)＋kπ(k∈Z)，解得x＝eq \f(3π,4ω)＋eq \f(kπ,ω)(k∈Z)．
当k＝0时，eq \f(3π,4ω)≤π，即eq \f(3,4)≤ω，
当k＝1时，eq \f(3π,4ω)＋eq \f(π,ω)≥2π，即ω≤eq \f(7,8).
综上，eq \f(3,4)≤ω≤eq \f(7,8).
(2)显然ω≠0，分两种情况：
若ω＞0，当x∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,3)，\f(π,4)))时，－eq \f(π,3)ω≤ωx≤eq \f(π,4)ω.
因函数f(x)＝2sin ωx在区间eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,3)，\f(π,4)))上的最小值为－2，所以－eq \f(π,3)ω≤－eq \f(π,2)，解得ω≥eq \f(3,2).
若ω＜0，当x∈eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,3)，\f(π,4)))时，eq \f(π,4)ω≤ωx≤－eq \f(π,3)ω，
因函数f(x)＝2sin ωx在区间eq \b\lc\[\rc\](\a\vs4\al\c1(－\f(π,3)，\f(π,4)))上的最小值为－2，所以eq \f(π,4)ω≤－eq \f(π,2)，解得ω≤－2.
综上所述，符合条件的实数ω≤－2或ω≥eq \f(3,2).]
[评析] 这类三角函数题除了需要熟练掌握正弦函数、余弦函数、正切函数的单调性外，还必须知晓一个周期里函数最值的变化，以及何时取到最值，函数取到最值的区间要求与题目给定的区间的关系如何.
y＝Asin(ωx＋φ)(A＞0，ω＞0，x≥0)表示一个简谐运动
振幅
周期
频率
相位
初相
A
T＝eq \f(2π,ω)
f＝eq \f(1,T)＝eq \f(ω,2π)
ωx＋φ
φ
x
－eq \f(φ,ω)
eq \f(\f(π,2)－φ,ω)
eq \f(π－φ,ω)
eq \f(\f(3,2)π－φ,ω)
eq \f(2π－φ,ω)
ωx＋φ
0
eq \f(π,2)
π
eq \f(3π,2)
2π
y＝Asin(ωx＋φ)
0
A
0
－A
0
月份x
1
2
3
4
收购价格y(元/斤)
6
7
6
5
课外素养提升⑤ 逻辑推理与数学运算——三角函数中ω的确定方法
三角函数的周期T与ω的关系
三角函数的单调性与ω的关系