





高中数学北师大版 (2019)选择性必修 第一册3.1 离散型随机变量的均值示范课ppt课件
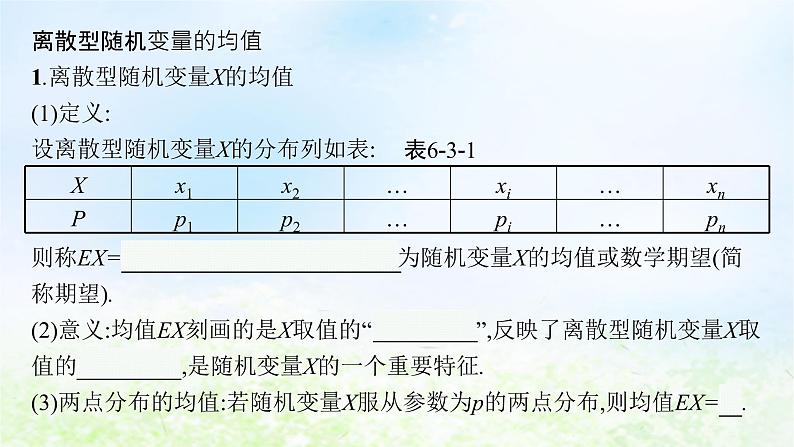
展开1.离散型随机变量X的均值(1)定义:设离散型随机变量X的分布列如表:则称EX= x1p1+x2p2+…+xipi+…+xnpn 为随机变量X的均值或数学期望(简称期望).(2)意义:均值EX刻画的是X取值的“ 中心位置 ”,反映了离散型随机变量X取值的 平均水平 ,是随机变量X的一个重要特征.(3)两点分布的均值:若随机变量X服从参数为p的两点分布,则均值EX= p .
若X为随机变量,则Y=aX+b(其中a,b为常数)也是随机变量,且P(Y=axi+b)=P(X=xi),i=1,2,3,…,n.EY=E(aX+b)=aEX+b.
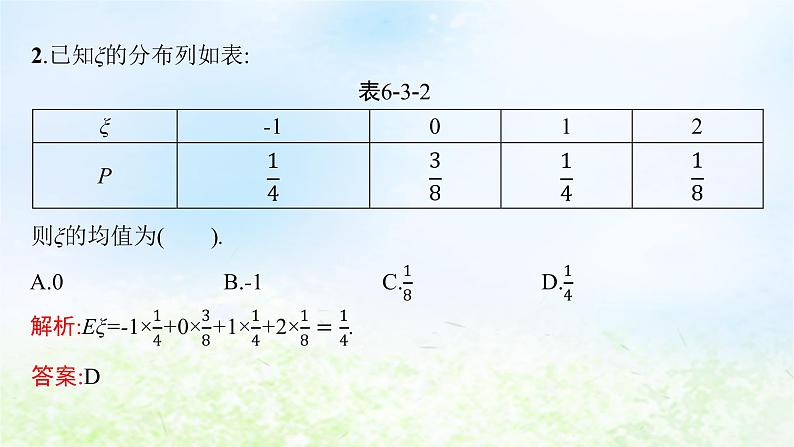
2.已知ξ的分布列如表:则ξ的均值为( ).
【例1】 在甲、乙等6个单位参加的一次演出活动中,每个单位的节目集中安排在一起,若采用抽签的方式随机确定各单位的演出顺序(序号为1,2,…,6),求:(1)甲、乙两单位的演出序号至少有一个为奇数的概率;(2)甲、乙两单位之间的演出单位个数ξ的分布列与均值.
解:只考虑甲、乙两单位的相对位置,故可用组合计算样本点数.(1)设A表示“甲、乙的演出序号至少有一个为奇数”,则 表示“甲、乙的演出序号均为偶数”,
本例条件不变,记甲单位的演出序号为x,乙单位的演出序号为y,随机变量η=x+y,求η的分布列和数学期望.
求离散型随机变量ξ的均值的步骤(1)根据ξ的实际意义,写出ξ的全部取值;(2)求出ξ取每个值的概率;(3)写出ξ的分布列;(4)利用定义求出均值.其中第(1)(2)两条是解答此类题目的关键,在求解过程中应注重分析概率的相关知识.
【例2】 已知随机变量X的分布列如表:(1)求m的值;(2)求EX;(3)若Y=2X-3,求EY.
1.该类题目属于已知离散型分布列求均值,求解方法是直接套用公式EX=x1p1+x2p2+…+xnpn求解.2.对于aX+b型的随机变量,可利用均值的性质求解,即E(aX+b)=aEX+b;也可以先列出aX+b的分布列,再用均值公式求解,比较两种方式显然前者较方便.
【例3】 随机抽取某厂的某种产品200件,经质检,其中一等品126件,二等品50件,三等品20件,次品4件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而生产1件次品亏损2万元,设生产1件产品的利润(单位:万元)为X.(1)求X的分布列;(2)求生产1件产品的平均利润(即X的均值);(3)经技术革新后,仍有四个等级的产品,但次品率降为1%,一等品率提高为70%,如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
(2)EX=6×0.63+2×0.25+1×0.1+(-2)×0.02=4.34(万元).(3)设技术革新后的三等品率为x,则此时生产1件产品的平均利润为EX=6×0.7+2×(1-0.7-0.01-x)+1×x+(-2)×0.01=4.76-x(万元) (0≤x≤0.29).依题意,EX≥4.73,即4.76-x≥4.73,解得x≤0.03,所以三等品率最多为3%.
高中数学北师大版 (2019)选择性必修 第一册3.1 离散型随机变量的均值教案配套课件ppt: 这是一份高中数学北师大版 (2019)选择性必修 第一册3.1 离散型随机变量的均值教案配套课件ppt,共36页。PPT课件主要包含了新知初探·课前预习,题型探究·课堂解透,平均水平,答案A,答案C,答案036,答案2376,易错警示,答案B,答案09等内容,欢迎下载使用。
北师大版 (2019)选择性必修 第一册3.1 离散型随机变量的均值作业ppt课件: 这是一份北师大版 (2019)选择性必修 第一册3.1 离散型随机变量的均值作业ppt课件,共21页。PPT课件主要包含了BCD等内容,欢迎下载使用。
高中数学北师大版 (2019)选择性必修 第一册第六章 概率3 离散型随机变量的均值与方差3.1 离散型随机变量的均值教学课件ppt: 这是一份高中数学北师大版 (2019)选择性必修 第一册第六章 概率3 离散型随机变量的均值与方差3.1 离散型随机变量的均值教学课件ppt,共35页。PPT课件主要包含了必备知识·探新知,知识点1,离散型随机变量的均值,平均取值,aEx+b,知识点2,两点分布的数学期望,关键能力·攻重难,典例1,典例2等内容,欢迎下载使用。













