



还剩15页未读,
继续阅读
所属成套资源:北师大版数学选择性必修第一册课件PPT全套
成套系列资料,整套一键下载
北师大版高中数学选择性必修第一册7-1-2一元线性回归方程第一课时课件
展开
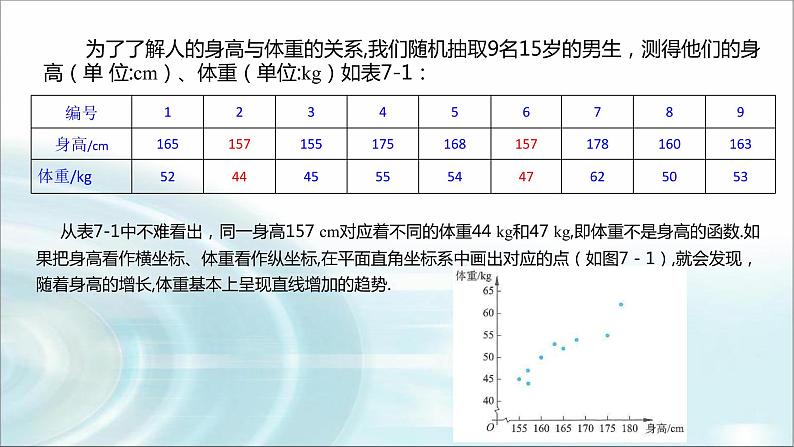
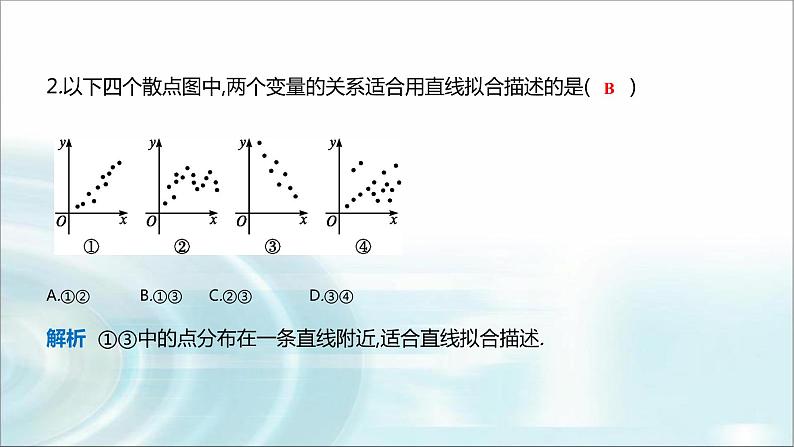
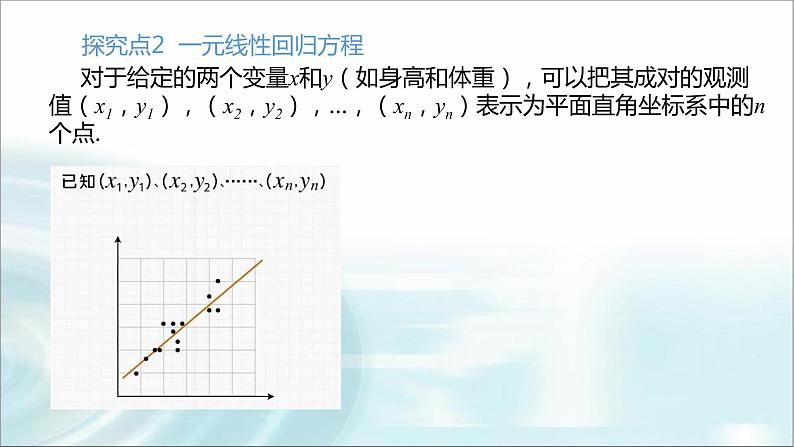
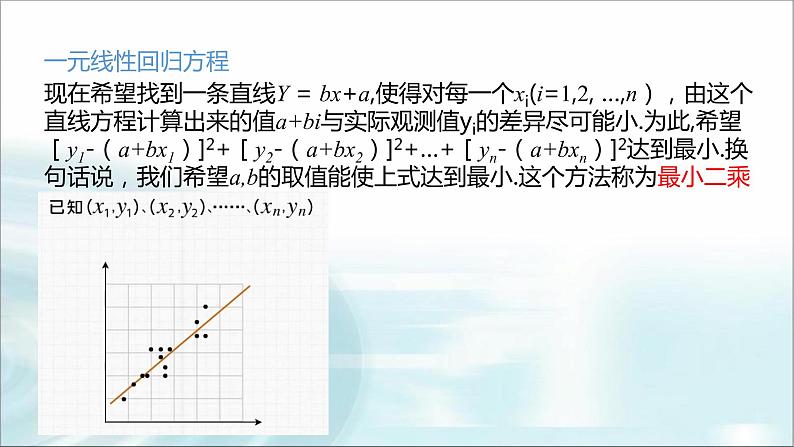
§1 第七章 案例统计§1 一元线性回归 1.1 直线拟合1.2一元线性回归方程(第一课时) 在现实生活中,反映量与量之间的函数关系非常普遍,但也存在一些量与量之间不满足函数关系,如人的身高与体重.一般说来,人的身高越高,体重就越重,二者确实有关系.但是身高相同的人,体重却不一定相同,也就是说,给定身高h没有唯一的体重m与之对应.在现实生活中,这样的例子还有很多,如人的年龄与血压、农作物的施肥量与产量等.探究点1 多直线拟合与曲线拟合探究导学为了了解人的身高与体重的关系,我们随机抽取9名15岁的男生,测得他们的身高(单 位:cm)、体重(单位:kg)如表7-1: 从表7-1中不难看出,同一身高157 cm对应着不同的体重44 kg和47 kg,即体重不是身高的函数.如果把身高看作横坐标、体重看作纵坐标,在平面直角坐标系中画出对应的点(如图7 - 1),就会发现,随着身高的增长,体重基本上呈现直线增加的趋势.1.在图7-1中,每个点对应的一对数据(xi, yi ),称为成对数据.这些点构成的图称为散点图.2.从散点图上可以看出,如果变量之间存在着某种关系,这些点会有一个大致趋势,这种趋势通常可以用一条光滑的曲线来近似地描述.这样近似描述的过程称为曲线拟合.3.若在两个变量x和y的散点图中,所有点看上去都在一条直线附近波动,此时就可以用一条直线 来近似地描述这两个量之间的关系,称之为直线拟合.2.以下四个散点图中,两个变量的关系适合用直线拟合描述的是( )A.①② B.①③ C.②③ D.③④解析 ①③中的点分布在一条直线附近,适合直线拟合描述.B探究点2 一元线性回归方程 对于给定的两个变量x和y(如身高和体重),可以把其成对的观测值(x1,y1),(x2,y2),…,(xn,yn)表示为平面直角坐标系中的n个点.一元线性回归方程现在希望找到一条直线Y = bx+a,使得对每一个xi(i=1,2, …,n),由这个直线方程计算出来的值a+bi与实际观测值yi的差异尽可能小.为此,希望[y1-(a+bx1)]2+[y2-(a+bx2)]2+…+[yn-(a+bxn)]2达到最小.换句话说,我们希望a,b的取值能使上式达到最小.这个方法称为最小二乘法.1.直线方程___________称作Y关于X的 ,相应的直线称作Y关于X的 , 是这个 .线性回归方程回归直线线性回归方程的系数 在这里需要强调的是:身高和体重之间并没有函数关系,我们得到的线性回归方程只是对其变化趋势的一种近似描述.对一个给定身高的人,人们可以用这个方程来估计这个人的体重,这是十分有意义的. 例1 在本章1.1节的练习中,从散点图可以看出,某小卖部6天卖出热茶的杯数Y(单位:杯)与当天气温X(单位:°C)之间存在近似的线性关系.数据如表7-2.(1)试用最小二乘法求岀Y关于X的线性回归方程;(2)如果某天的气温是-3℃,请预测这天可能会卖出热茶多少杯. D§1一课一练 149 第3题§1一课一练 149页 第5题§1一课一练 150页 第13题§1一课一练 155页 第2题§1 第七章 案例统计§2成对数据的线性相关性2.1 相关系数2.2成对数据的线性相关性分析 样本(线性)相关系数r的取值范围为[―1,1]. | r |值越接近1,随机变量之间的线性相关程度越强;| r |值越接近0,随机变量之间的线性相关程度越弱. 当r>0时,两个随机变量的值总体上变化趋势相同,此时称两个随机变量正相关; 当r<0时,两个随机变量的值总体上变化趋势相反,此时称两个随机变量负相关; 当r=0时,此时称两个随机变量线性不相关. 1.判断变量间的相关关系例1 解析:由这两个散点图可以判断,变量x与y负相关,u与v正相关.答案:CAC§1一课一练 166页 第5题
相关资料
更多









