

还剩16页未读,
继续阅读
成套系列资料,整套一键下载
北师大版高中数学选择性必修第一册直线与圆的位置关系学案含解析
展开
专题10 直线与圆的位置关系
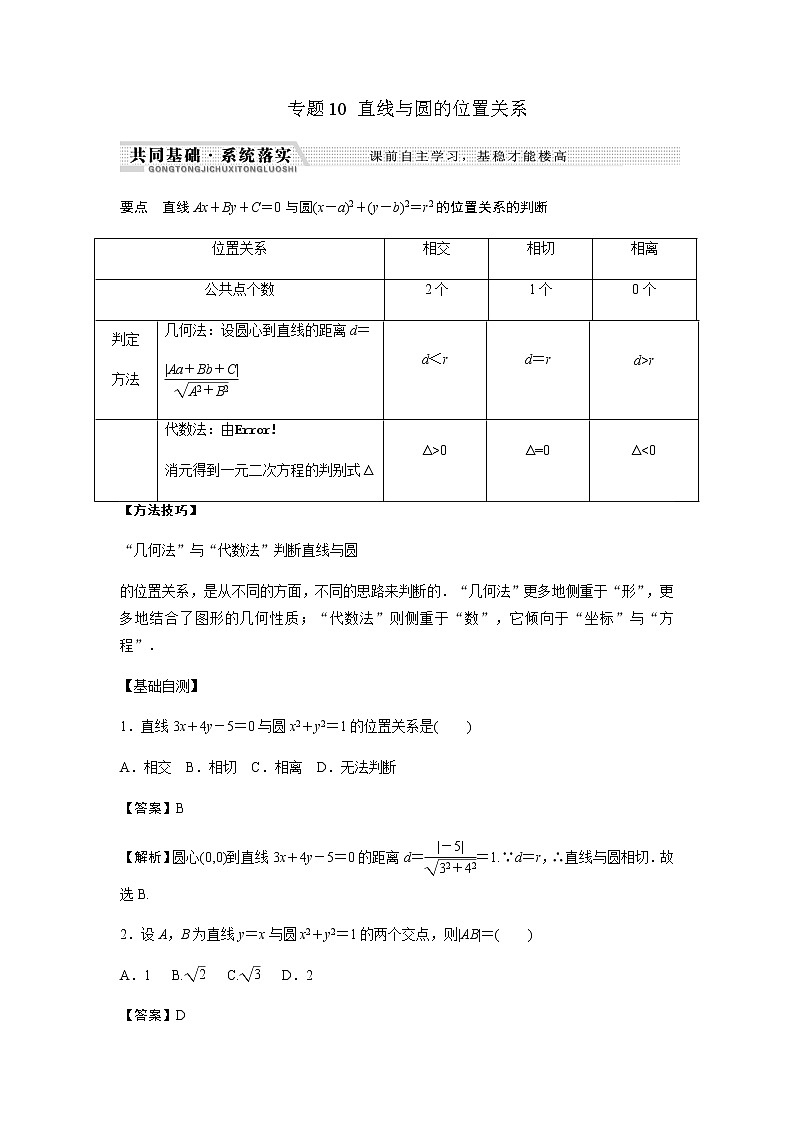
要点 直线Ax+By+C=0与圆(x-a)2+(y-b)2=r2的位置关系的判断
位置关系
相交
相切
相离
公共点个数
2个
1个
0个
判定
方法
几何法:设圆心到直线的距离d=
d<r
d=r
d>r
代数法:由
消元得到一元二次方程的判别式Δ
Δ>0
Δ=0
Δ<0
【方法技巧】
“几何法”与“代数法”判断直线与圆
的位置关系,是从不同的方面,不同的思路来判断的.“几何法”更多地侧重于“形”,更多地结合了图形的几何性质;“代数法”则侧重于“数”,它倾向于“坐标”与“方程”.
【基础自测】
1.直线3x+4y-5=0与圆x2+y2=1的位置关系是( )
A.相交 B.相切 C.相离 D.无法判断
【答案】B
【解析】圆心(0,0)到直线3x+4y-5=0的距离d==1.∵d=r,∴直线与圆相切.故选B.
2.设A,B为直线y=x与圆x2+y2=1的两个交点,则|AB|=( )
A.1 B. C. D.2
【答案】D
【解析】直线y=x过圆x2+y2=1的圆心C(0,0),则|AB|=2,故选D.
3.直线x+2y=0被圆C:x2+y2-6x-2y-15=0所截得的弦长等于________.
【答案】4
【解析】由已知圆心C(3,1),半径r=5.又圆心C到直线l的距离d==,则弦长=2=4.
题型一 直线与圆位置关系的判断
1.直线y=x+1与圆x2+y2=1的位置关系为( )
A.相切 B.相交但直线不过圆心 C.直线过圆心 D.相离
【答案】B
【解析】圆心(0,0)到直线y=x+1的距离d==.因为0<<1,故直线与圆相交但直线不过圆心,故选B.
2.已知圆C:x2+y2-4x=0,l是过点P(3,0)的直线,则( )
A.l与C相交 B.l与C相切 C.l与C相离 D.以上三个选项均有可能
【答案】A
【解析】将点P(3,0)的坐标代入圆的方程,得32+02-4×3=9-12=-3<0,∴点P(3,0)在圆内.
∴过点P的直线l必与圆C相交.故选A.
3.已知直线方程mx-y-m-1=0,圆的方程x2+y2-4x-2y+1=0.
若直线与圆相切,则m=________;
若直线与圆相离,则m的范围是________.
【答案】0或-,(-,0)
【解析】已知圆的标准方程为(x-2)2+(y-1)2=4,
即圆心为C(2,1),半径r=2
圆心C(2,1)到直线mx-y-m-1=0的距离d=.
若直线与圆相切,则d==r=2
解得m=0或m=-.
若直线与圆相离,则d>2,即-
判断直线与圆位置关系的三种方法
1.几何法:由圆心到直线的距离d与圆的半径r的大小关系判断.
2.代数法:根据直线与圆的方程组成的方程组解的个数来判断.
3.直线系法:若直线恒过定点,可通过判断点与圆的位置关系判断,但有一定的局限性,必须是过定点的直线系.
题型二 有关圆的切线问题
【例1】过点A(4,-3)作圆(x-3)2+(y-1)2=1的切线,求此切线方程.
【解析】因为(4-3)2+(-3-1)2=17>1,
所以点A在圆外,故切线有两条.
①若所求直线的斜率存在,设切线斜率为k,
则切线方程为y+3=k(x-4),即kx-y-4k-3=0.
设圆心为C,
因为圆心C(3,1)到切线的距离等于半径1,
所以=1,即|k+4|=,
所以k2+8k+16=k2+1,解得k=-.
所以切线方程为-x-y+-3=0,
即15x+8y-36=0.
②若直线斜率不存在,
圆心C(3,1)到直线x=4的距离为1,
这时直线x=4与圆相切,所以另一条切线方程为x=4.
综上,所求切线方程为15x+8y-36=0或x=4.
【方法技巧】
圆的切线的求法
1.点在圆上时:
求过圆上一点(x0,y0)的圆的切线方程:先求切点与圆心连线的斜率k,再由垂直关系得切线的斜率为-,由点斜式可得切线方程.如果斜率为零或不存在,则由图形可直接得切线方程x=x0或y=y0.
2.点在圆外时:
(1)几何法:设切线方程为y-y0=k(x-x0).由圆心到直线的距离等于半径,可求得k,也就是切线方程.
(2)代数法:设切线方程为y-y0=k(x-x0),与圆的方程联立,消去y后得到关于x的一元二次方程,由Δ=0求出k,可得切线方程.
特别注意:切线的斜率不存在的情况,不要漏解.
【变式训练】
1. 直线x+y+m=0与圆x2+y2=m相切,则m的值为( )
A.0或2 B.2 C. D.无解
【答案】B
【解析】由于直线与圆相切,故=,解得m=0(舍去)或m=2.故选B.
2.过点A(2,1),作圆的(x-3)2+(y-1)2=1切线,则切线方程为________.
【答案】(2)y=1
【解析】(2)因为(2-3)2+(1-1)2=1,所以点A(2,1)在圆上,从而A是切点,又过圆心(3,1)与点A的直线斜率为0,故所求切线的方程为y=1.
3. (多填题)已知圆C的圆心坐标是(0,m),半径长是r.若直线2x-y+3=0与圆C相切于点A(-2,-1),则m=______,r=________.
【答案】(3)-2,
【解析】法一:由题意得,圆心C(0,m)到直线2x-y+3=0的距离d==r,又r=|AC|=,所以=,解得m=-2,所以r=.
法二:根据题意画出图形,可知
A(-2,-1),C(0,m),B(0,3),
则|AB|==2,
|AC|==,
|BC|=|m-3|.
∵直线2x-y+3=0与圆C相切于点A,
∴∠BAC=90°,
∴|AB|2+|AC|2=|BC|2.
即20+4+(m+1)2=(m-3)2,
解得m=-2.
∴r=|AC|==.
题型三 有关圆的弦长问题
【例2】求直线l:3x+y-6=0被圆C:x2+y2-2y-4=0截得的弦长.
【分析】弦心距、半弦长与直径构成的直角三角形求解
【解析】法一:圆C:x2+y2-2y-4=0
可化为x2+(y-1)2=5,
其圆心坐标为(0,1),半径r=.
点(0,1)到直线l的距离为d==,
l=2=,所以截得的弦长为.
法二:设直线l与圆C交于A、B两点.
由得交点A(1,3),B(2,0),
所以弦AB的长为|AB|==.
【变式探究】若本例改为“过点(2,0)的直线被圆C:x2+y2-2y-4=0截得的弦长为,求该直线方程”,又如何求解?
【解析】由例题知,圆心C(0,1),半径r=,又弦长为,所以圆心到直线的距离
d===.
又直线过点(2,0),知直线斜率一定存在,
可设直线斜率为k,则直线方程为y=k(x-2),
所以d==,解得k=-3或k=,
所以直线方程为y=-3(x-2)或y=(x-2),
即3x+y-6=0或x-3y-2=0.
【方法技巧】
求弦长常用的三种方法
1.利用圆的半径r,圆心到直线的距离d,弦长l之间的关系(l)2+d2=r2解题.
2.利用交点坐标,若直线与圆的交点坐标易求出,求出交点坐标后,直接用两点间距离公式计算弦长.
3.利用弦长公式,设直线l:y=kx+b,与圆的两交点(x1,y1),(x2,y2),将直线方程代入圆的方程,消元后利用根与系数的关系得弦长
l=|x1-x2|=.
【变式训练】
1.过点(3,1)作圆(x-2)2+(y-2)2=4的弦,其中最短弦的长为________.
【答案】(1)2
【解析】(1)设点A(3,1),易知圆心C(2,2),半径r=2.当弦过点A(3,1)且与CA垂直时为最短弦,|CA|==,∴半弦长===,∴最短弦的长为2.
2.已知圆C的圆心与点P(-2,1)关于直线y=x+1对称,直线3x+4y-11=0与圆C相交于A,B两点,且|AB|=6,求圆C的方程.
【答案】(2)x2+(y+1)2=18
【解析】(2)设点P关于直线y=x+1的对称点为C(m,n),
则由⇒
故圆心C到直线3x+4y-11=0的距离
d==3,
所以圆C的半径的平方r2=d2+=18.
故圆C的方程为x2+(y+1)2=18.
题型四 直线与圆的方程的实际应用
【例3】为了适应市场需要,某地准备建一个圆形生猪储备基地(如图),它的附近有一条公路,从基地中心O处向东走1 km是储备基地的边界上的点A,接着向东再走7 km到达公路上的点B;从基地中心O向正北走8 km到达公路上的另一点C.现准备在储备基地的边界上选一点D,修建一条由D通往公路BC的专用线DE,求DE的最短距离.
【分析】建系→求圆O与直线BC的方程→利用直线与圆的位置关系求解.
【解析】以O为坐标原点,OB,OC所在的直线分别为x轴和y轴,建立平面直角坐标系,则圆O的方程为x2+y2=1.
因为点B(8,0),C(0,8),所以直线BC的方程为+=1,即x+y=8.
当点D选在与直线BC平行的直线(距BC较近的一条)与圆相切所成的切点处时,DE为最短距离.此时DE的最小值为-1=(4-1) km.
即DE的最短距离为(4-1) km.
【方法技巧】
求解直线与圆的方程的实际应用问题的四个步骤
1.认真审题,明确题意.
2.建立平面直角坐标系,用方程表示直线和圆,从而在实际问题中建立直线与圆的方程.
3.利用直线与圆的方程的有关知识求解问题.
4.把代数结果还原为实际问题的解释.
【变式训练】
1.台风中心从A地以20千米/时的速度向东北方向移动,离台风中心30千米内的地区为危险区,城市B在A的正东40千米处,B城市处于危险区内的时间为( )
A.0.5小时 B.1小时 C.1.5小时 D.2小时
【答案】(1)B
【解析】(1)以台风中心A为坐标原点建立平面直角坐标系,如图,
则台风中心在直线y=x上移动,又B(40,0)到y=x的距离为d=20,由|BE|=|BF|=30知|EF|=20,即台风中心从E到F时,B城市处于危险区内,时间为t==1小时.故选B.
2.如图为一座圆拱桥的截面图,当水面在某位置时,拱顶离水面2 m,水面宽12 m,当水面下降1 m后,水面宽为________m.
【答案】(1)B (2)2
【解析】(2)如图,以圆拱桥顶为坐标原点,以过圆拱顶点的竖直直线为y轴,建立平面直角坐标系.
设圆心为C,圆的方程为x2+(y+r)2=r2(r>0),水面所在弦的端点为A,B,则A(6,-2).将点A(6,-2)代入圆的方程,得r=10,
∴圆的方程为x2+(y+10)2=100.当水面下降1 m后,可设点A′(x0,-3)(x0>0),
将A′(x0,-3)代入圆的方程,得x0=,
∴当水面下降1 m后,水面宽为2x0=2(m).
【易错辨析】忽略了圆的一个隐含条件
【例4】已知圆的方程为x2+y2+ax+2y+a2=0,一定点A(1,2),要使过定点A(1,2)作圆的切线有两条,则a的取值范围为________.
【解析】圆的标准方程为(x+)2+(y+1)2=,圆心C坐标为(-,-1),半径r==,则4-3a2>0,解得-
化简得a2+a+9>0,不等式a2+a+9>0恒成立,
故a的取值范围是(-,)
【易错警示】
易错原因
纠错心得
忽视了圆的方程x2+y2+ax+2y+a2=0中有一个隐含条件,即D2+E2-4F>0
同学们在解答含有参数的问题时,要多一些严谨,以免遗漏某些条件,导致结果出错.
1.(2020·大埔县虎山中学高二期中)直线l: y-1=k(x-1)和圆x2+y2-2y=0的关系是( )
A.相离 B.相切或相交
C.相交 D.相切
【答案】C
【解析】l过定点A(1,1),∵12+12-2×1=0,∴点A在圆上,∵直线x=1过点A且为圆的切线,又l斜率存在,∴l与圆一定相交,故选C.
2.(2020·天津一中高二期末)若直线x-y=2被圆(x-a)2+y2=4所截得的弦长为2,则实数a的值为( )
A.0或4 B.0或3
C.-2或6 D.-1或
【答案】A
【解析】由圆的方程,可知圆心坐标为(a,0),半径r=2.又直线被圆截得的弦长为2,所以圆心到直线的距离d==.又d=,所以|a-2|=2,解得a=4或a=0.故选A.
3.(2020·江西南昌二中高二月考)由直线y=x+1上的一点向圆(x-3)2+y2=1引切线,则切线长的最小值为( )
A.1 B.2
C. D.3
【答案】C
【解析】因为切线长的最小值是当直线y=x+1上的点与圆心距离最小时取得,圆心(3,0)到直线y=x+1的距离为d==2,圆的半径为1,所以切线长的最小值为==,故选C.
4.(多选) (2020·山东潍坊第一中学高二月考)与圆C:x2+y2-4x+2=0相切,且在x,y轴上的截距相等的直线方程为( )
A.x+y=0 B.x-y=0
C.x=0 D.x+y=4
【答案】ABD
【解析】圆C的方程可化为(x-2)2+y2=2.可分为两种情况讨论:
(1)直线在x,y轴上的截距均为0,易知直线斜率必存在,设直线方程为y=kx,则=,解得k=±1;
(2)直线在x,y轴上的截距均不为0,则可设直线方程为+=1(a≠0),即x+y-a=0(a≠0),则=,解得a=4(a=0舍去).
5.(2020·山东省郓城第一中学高二月考)一辆卡车宽1.6米,要经过一个半径为3.6米的半圆形隧道,则这辆卡车的平顶车蓬蓬顶距地面的高度不得超过( )
A.1.4米 B.3.5米
C.3.6米 D.2米
【答案】B
【解析】建立如图所示的平面直角坐标系.如图设蓬顶距地面高度为h,则A(0.8,h-3.6)所在圆的方程为: x2+(y+3.6)2=3.62,把A(0.8,h-3.6)代入得0.82+h2=3.62.∴h=4≈3.5(米).
6.(2020·五莲县教学研究室高二期中)若点P(1,2)在以坐标原点为圆心的圆上,则该圆在点P处的切线方程为________.
【答案】x+2y-5=0
【解析】设切线斜率为k,则由已知得: k·kOP=-1.
∴k=-.∴切线方程为x+2y-5=0.
7.(2020·重庆市万州沙河中学高二月考)已知圆C的圆心是直线x-y+1=0与x轴的交点,且圆C与直线x+y+3=0相切,则圆C的方程为____________________.
【答案】 (x+1)2+y2=2
【解析】令y=0得x=-1,所以直线x-y+1=0与x轴的交点为(-1,0).因为直线x+y+3=0与圆相切,
所以圆心到直线的距离等于半径,
即r==,
所以圆C的方程为(x+1)2+y2=2.
8.(2020·江苏省南通中学高二期中)点M,N在圆x2+y2+kx+2y+4=0上,且点M,N关于直线x-y+1=0对称,则该圆的半径是________.
【答案】1
【解析】由题知,直线x-y+1=0过圆心,
即-+1+1=0,∴k=4.∴r==1.
9.(2020·苏州市相城区陆慕高级中学高二月考)已知直线方程mx-y-m-1=0,圆的方程x2+y2-4x-2y+1=0.当m为何值时,圆与直线:
(1)有两个公共点;
(2)只有一个公共点;
(3)没有公共点.
【解析】法一:将直线mx-y-m-1=0代入圆的方程化简整理得,
(1+m2)x2-2(m2+2m+2)x+m2+4m+4=0.
则Δ=4m(3m+4).
(1)当Δ>0,即m>0或m<-时,直线与圆相交,即直线与圆有两个公共点;
(2)当Δ=0,即m=0或m=-时,直线与圆相切,即直线与圆只有一个公共点;
(3)当Δ<0,即-
即圆心为C(2,1),半径r=2.
圆心C(2,1)到直线mx-y-m-1=0的距离
d== .
(1)当d<2,即m>0或m<-时,直线与圆相交,即直线与圆有两个公共点;
(2)当d=2,即m=0或m=-时,直线与圆相切,即直线与圆只有一个公共点;
(3)当d>2,即-
(1)求圆A的方程;
(2)当|MN|=2时,求直线l的方程.
【解析】(1)设圆A的半径为r.∵圆A与直线l1:x+2y+7=0相切,∴r==2.
∴圆A的方程为(x+1)2+(y-2)2=20.
(2)①当直线l与x轴垂直时,直线l的方程为x=-2,
易得|MN|=2,符合题意;
②当直线l与x轴不垂直时,
设直线l的方程为y=k(x+2),即kx-y+2k=0.
取MN的中点Q,连接AQ,则AQ⊥MN.
∵|MN|=2,∴|AQ|==1,
∴=1,得k=,
∴直线l的方程为3x-4y+6=0.
综上,直线l的方程为x=-2或3x-4y+6=0.
11. (2020·运城市景胜中学高二期中)瑞士数学家欧拉(LeonhardEuler)1765年在其所著的《三角形的几何学》一书中提出:任意三角形的外心、重心、垂心在同一条直线上,后人称这条直线为欧拉线.已知的顶点,,其欧拉线方程为,则顶点的坐标可以是( )
A. B. C. D.
【答案】AD
【解析】设的垂直平分线为,
的外心为欧拉线方程为
与直线的交点为,
,①
由,,重心为,
代入欧拉线方程,得,②
由 ①②可得或 .故选:AD
12. (2020·宜宾市叙州区第一中学校高二月考)设有一组圆:().下列四个命题中真命题的是( )
A.存在一条定直线与所有的圆均相切
B.存在一条定直线与所有的圆均相交
C.存在一条定直线与所有的圆均不相交
D.所有的圆均不经过原点
【答案】BD
【解析】圆心为,半径为,
,,,,,圆与圆是内含关系,因此不可能有直线与这两个圆都相切,从而A错误;
易知圆心在直线上,此直线与所有圆都相交,B正确;
若取无穷大,则所有直线都与圆相交,C错;
将代入圆方程得,即,等式左边是奇数,右边是偶数,因此方程无整数解,即原点不在任一圆上,D正确.故选:BD.
13.(2020·四川邻水实验学校高二期中)过原点O作圆x2+y2-6x-8y+20=0的两条切线,设切点分别为P,Q,则线段PQ的长为________.
【答案】4
【解析】圆的方程化为标准方程为(x-3)2+(y-4)2=5,示意图如图所示.则圆心为O′(3,4),r=.切线长|OP|==2.
∴|PQ|=2·=2×=4.
14. (2020·福建厦门双十中学高二月考)已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的右上方.
(1)求圆C的方程;
(2)过点M(1,0)的直线与圆C交于A,B两点(A在x轴上方),问在x轴正半轴上是否存在定点N,使得x轴平分∠ANB?若存在,请求出点N的坐标;若不存在,请说明理由.
【解析】(1)设圆心C(a,0),则=2⇒a=0或a=-5(舍).所以圆C:x2+y2=4.
(2)当直线AB⊥x轴时,x轴平分∠ANB.
当直线AB的斜率存在时,设直线AB的方程为y=k(x-1),N(t,0),A(x1,y1),B(x2,y2),
由得,(k2+1)x2-2k2x+k2-4=0,
所以x1+x2=,x1x2=.若x轴平分∠ANB,则kAN=-kBN⇒+=0⇒+=0⇒2x1x2-(t+1)(x1+x2)+2t=0⇒-+2t=0⇒t=4,
所以当点N为(4,0)时,能使得∠ANM=∠BNM总成立.
15.(2020·湖北高二期中)在①圆经过,②圆心在直线上,③圆截轴所得弦长为8且圆心的坐标为整数;这三个条件中任选一个,补充在下面的问题中,进行求解.
已知圆经过点,且______;
(1)求圆的方程;
(2)已知直线经过点,直线与圆相交所得的弦长为8,求直线的方程.
【答案】B
【解析】选条件①,
(1)设圆的方程为,
依题意有,
解得,,,
所以圆的方程为,
即圆的标准方程为:.
(2)设圆心到直线的距离为,
则弦长,
当直线的斜率不存在时,,所以直线的斜率存在,
设其方程为,即,
,解得,,
所以所求直线的方程为或.
选条件②,
(1)设圆的方程为,
因为圆经过点,,且圆心在直线上
依题意有,
解得,,,
所以圆的方程为.
(2)设圆心到直线的距离为,
则弦长,
当直线的斜率不存在时,,所以直线的斜率存在,
设其方程为,即,
,解得,,
所以所求直线的方程为或.
选条件③,
设圆的方程为,
由圆经过点,,故,
又因为圆截轴所得弦长为8,
故方程的两个实数根的差的绝对值为.
所以,即
解方程组,
得,,或,,,
由于圆心的坐标为整数,
故圆的方程为
(2)设圆心到直线的距离为,
则弦长,
当直线的斜率不存在时,,所以直线的斜率存在,
设其方程为,即,
,解得,,
所以所求直线的方程为或.
要点 直线Ax+By+C=0与圆(x-a)2+(y-b)2=r2的位置关系的判断
位置关系
相交
相切
相离
公共点个数
2个
1个
0个
判定
方法
几何法:设圆心到直线的距离d=
d<r
d=r
d>r
代数法:由
消元得到一元二次方程的判别式Δ
Δ>0
Δ=0
Δ<0
【方法技巧】
“几何法”与“代数法”判断直线与圆
的位置关系,是从不同的方面,不同的思路来判断的.“几何法”更多地侧重于“形”,更多地结合了图形的几何性质;“代数法”则侧重于“数”,它倾向于“坐标”与“方程”.
【基础自测】
1.直线3x+4y-5=0与圆x2+y2=1的位置关系是( )
A.相交 B.相切 C.相离 D.无法判断
【答案】B
【解析】圆心(0,0)到直线3x+4y-5=0的距离d==1.∵d=r,∴直线与圆相切.故选B.
2.设A,B为直线y=x与圆x2+y2=1的两个交点,则|AB|=( )
A.1 B. C. D.2
【答案】D
【解析】直线y=x过圆x2+y2=1的圆心C(0,0),则|AB|=2,故选D.
3.直线x+2y=0被圆C:x2+y2-6x-2y-15=0所截得的弦长等于________.
【答案】4
【解析】由已知圆心C(3,1),半径r=5.又圆心C到直线l的距离d==,则弦长=2=4.
题型一 直线与圆位置关系的判断
1.直线y=x+1与圆x2+y2=1的位置关系为( )
A.相切 B.相交但直线不过圆心 C.直线过圆心 D.相离
【答案】B
【解析】圆心(0,0)到直线y=x+1的距离d==.因为0<<1,故直线与圆相交但直线不过圆心,故选B.
2.已知圆C:x2+y2-4x=0,l是过点P(3,0)的直线,则( )
A.l与C相交 B.l与C相切 C.l与C相离 D.以上三个选项均有可能
【答案】A
【解析】将点P(3,0)的坐标代入圆的方程,得32+02-4×3=9-12=-3<0,∴点P(3,0)在圆内.
∴过点P的直线l必与圆C相交.故选A.
3.已知直线方程mx-y-m-1=0,圆的方程x2+y2-4x-2y+1=0.
若直线与圆相切,则m=________;
若直线与圆相离,则m的范围是________.
【答案】0或-,(-,0)
【解析】已知圆的标准方程为(x-2)2+(y-1)2=4,
即圆心为C(2,1),半径r=2
圆心C(2,1)到直线mx-y-m-1=0的距离d=.
若直线与圆相切,则d==r=2
解得m=0或m=-.
若直线与圆相离,则d>2,即-
判断直线与圆位置关系的三种方法
1.几何法:由圆心到直线的距离d与圆的半径r的大小关系判断.
2.代数法:根据直线与圆的方程组成的方程组解的个数来判断.
3.直线系法:若直线恒过定点,可通过判断点与圆的位置关系判断,但有一定的局限性,必须是过定点的直线系.
题型二 有关圆的切线问题
【例1】过点A(4,-3)作圆(x-3)2+(y-1)2=1的切线,求此切线方程.
【解析】因为(4-3)2+(-3-1)2=17>1,
所以点A在圆外,故切线有两条.
①若所求直线的斜率存在,设切线斜率为k,
则切线方程为y+3=k(x-4),即kx-y-4k-3=0.
设圆心为C,
因为圆心C(3,1)到切线的距离等于半径1,
所以=1,即|k+4|=,
所以k2+8k+16=k2+1,解得k=-.
所以切线方程为-x-y+-3=0,
即15x+8y-36=0.
②若直线斜率不存在,
圆心C(3,1)到直线x=4的距离为1,
这时直线x=4与圆相切,所以另一条切线方程为x=4.
综上,所求切线方程为15x+8y-36=0或x=4.
【方法技巧】
圆的切线的求法
1.点在圆上时:
求过圆上一点(x0,y0)的圆的切线方程:先求切点与圆心连线的斜率k,再由垂直关系得切线的斜率为-,由点斜式可得切线方程.如果斜率为零或不存在,则由图形可直接得切线方程x=x0或y=y0.
2.点在圆外时:
(1)几何法:设切线方程为y-y0=k(x-x0).由圆心到直线的距离等于半径,可求得k,也就是切线方程.
(2)代数法:设切线方程为y-y0=k(x-x0),与圆的方程联立,消去y后得到关于x的一元二次方程,由Δ=0求出k,可得切线方程.
特别注意:切线的斜率不存在的情况,不要漏解.
【变式训练】
1. 直线x+y+m=0与圆x2+y2=m相切,则m的值为( )
A.0或2 B.2 C. D.无解
【答案】B
【解析】由于直线与圆相切,故=,解得m=0(舍去)或m=2.故选B.
2.过点A(2,1),作圆的(x-3)2+(y-1)2=1切线,则切线方程为________.
【答案】(2)y=1
【解析】(2)因为(2-3)2+(1-1)2=1,所以点A(2,1)在圆上,从而A是切点,又过圆心(3,1)与点A的直线斜率为0,故所求切线的方程为y=1.
3. (多填题)已知圆C的圆心坐标是(0,m),半径长是r.若直线2x-y+3=0与圆C相切于点A(-2,-1),则m=______,r=________.
【答案】(3)-2,
【解析】法一:由题意得,圆心C(0,m)到直线2x-y+3=0的距离d==r,又r=|AC|=,所以=,解得m=-2,所以r=.
法二:根据题意画出图形,可知
A(-2,-1),C(0,m),B(0,3),
则|AB|==2,
|AC|==,
|BC|=|m-3|.
∵直线2x-y+3=0与圆C相切于点A,
∴∠BAC=90°,
∴|AB|2+|AC|2=|BC|2.
即20+4+(m+1)2=(m-3)2,
解得m=-2.
∴r=|AC|==.
题型三 有关圆的弦长问题
【例2】求直线l:3x+y-6=0被圆C:x2+y2-2y-4=0截得的弦长.
【分析】弦心距、半弦长与直径构成的直角三角形求解
【解析】法一:圆C:x2+y2-2y-4=0
可化为x2+(y-1)2=5,
其圆心坐标为(0,1),半径r=.
点(0,1)到直线l的距离为d==,
l=2=,所以截得的弦长为.
法二:设直线l与圆C交于A、B两点.
由得交点A(1,3),B(2,0),
所以弦AB的长为|AB|==.
【变式探究】若本例改为“过点(2,0)的直线被圆C:x2+y2-2y-4=0截得的弦长为,求该直线方程”,又如何求解?
【解析】由例题知,圆心C(0,1),半径r=,又弦长为,所以圆心到直线的距离
d===.
又直线过点(2,0),知直线斜率一定存在,
可设直线斜率为k,则直线方程为y=k(x-2),
所以d==,解得k=-3或k=,
所以直线方程为y=-3(x-2)或y=(x-2),
即3x+y-6=0或x-3y-2=0.
【方法技巧】
求弦长常用的三种方法
1.利用圆的半径r,圆心到直线的距离d,弦长l之间的关系(l)2+d2=r2解题.
2.利用交点坐标,若直线与圆的交点坐标易求出,求出交点坐标后,直接用两点间距离公式计算弦长.
3.利用弦长公式,设直线l:y=kx+b,与圆的两交点(x1,y1),(x2,y2),将直线方程代入圆的方程,消元后利用根与系数的关系得弦长
l=|x1-x2|=.
【变式训练】
1.过点(3,1)作圆(x-2)2+(y-2)2=4的弦,其中最短弦的长为________.
【答案】(1)2
【解析】(1)设点A(3,1),易知圆心C(2,2),半径r=2.当弦过点A(3,1)且与CA垂直时为最短弦,|CA|==,∴半弦长===,∴最短弦的长为2.
2.已知圆C的圆心与点P(-2,1)关于直线y=x+1对称,直线3x+4y-11=0与圆C相交于A,B两点,且|AB|=6,求圆C的方程.
【答案】(2)x2+(y+1)2=18
【解析】(2)设点P关于直线y=x+1的对称点为C(m,n),
则由⇒
故圆心C到直线3x+4y-11=0的距离
d==3,
所以圆C的半径的平方r2=d2+=18.
故圆C的方程为x2+(y+1)2=18.
题型四 直线与圆的方程的实际应用
【例3】为了适应市场需要,某地准备建一个圆形生猪储备基地(如图),它的附近有一条公路,从基地中心O处向东走1 km是储备基地的边界上的点A,接着向东再走7 km到达公路上的点B;从基地中心O向正北走8 km到达公路上的另一点C.现准备在储备基地的边界上选一点D,修建一条由D通往公路BC的专用线DE,求DE的最短距离.
【分析】建系→求圆O与直线BC的方程→利用直线与圆的位置关系求解.
【解析】以O为坐标原点,OB,OC所在的直线分别为x轴和y轴,建立平面直角坐标系,则圆O的方程为x2+y2=1.
因为点B(8,0),C(0,8),所以直线BC的方程为+=1,即x+y=8.
当点D选在与直线BC平行的直线(距BC较近的一条)与圆相切所成的切点处时,DE为最短距离.此时DE的最小值为-1=(4-1) km.
即DE的最短距离为(4-1) km.
【方法技巧】
求解直线与圆的方程的实际应用问题的四个步骤
1.认真审题,明确题意.
2.建立平面直角坐标系,用方程表示直线和圆,从而在实际问题中建立直线与圆的方程.
3.利用直线与圆的方程的有关知识求解问题.
4.把代数结果还原为实际问题的解释.
【变式训练】
1.台风中心从A地以20千米/时的速度向东北方向移动,离台风中心30千米内的地区为危险区,城市B在A的正东40千米处,B城市处于危险区内的时间为( )
A.0.5小时 B.1小时 C.1.5小时 D.2小时
【答案】(1)B
【解析】(1)以台风中心A为坐标原点建立平面直角坐标系,如图,
则台风中心在直线y=x上移动,又B(40,0)到y=x的距离为d=20,由|BE|=|BF|=30知|EF|=20,即台风中心从E到F时,B城市处于危险区内,时间为t==1小时.故选B.
2.如图为一座圆拱桥的截面图,当水面在某位置时,拱顶离水面2 m,水面宽12 m,当水面下降1 m后,水面宽为________m.
【答案】(1)B (2)2
【解析】(2)如图,以圆拱桥顶为坐标原点,以过圆拱顶点的竖直直线为y轴,建立平面直角坐标系.
设圆心为C,圆的方程为x2+(y+r)2=r2(r>0),水面所在弦的端点为A,B,则A(6,-2).将点A(6,-2)代入圆的方程,得r=10,
∴圆的方程为x2+(y+10)2=100.当水面下降1 m后,可设点A′(x0,-3)(x0>0),
将A′(x0,-3)代入圆的方程,得x0=,
∴当水面下降1 m后,水面宽为2x0=2(m).
【易错辨析】忽略了圆的一个隐含条件
【例4】已知圆的方程为x2+y2+ax+2y+a2=0,一定点A(1,2),要使过定点A(1,2)作圆的切线有两条,则a的取值范围为________.
【解析】圆的标准方程为(x+)2+(y+1)2=,圆心C坐标为(-,-1),半径r==,则4-3a2>0,解得-
化简得a2+a+9>0,不等式a2+a+9>0恒成立,
故a的取值范围是(-,)
【易错警示】
易错原因
纠错心得
忽视了圆的方程x2+y2+ax+2y+a2=0中有一个隐含条件,即D2+E2-4F>0
同学们在解答含有参数的问题时,要多一些严谨,以免遗漏某些条件,导致结果出错.
1.(2020·大埔县虎山中学高二期中)直线l: y-1=k(x-1)和圆x2+y2-2y=0的关系是( )
A.相离 B.相切或相交
C.相交 D.相切
【答案】C
【解析】l过定点A(1,1),∵12+12-2×1=0,∴点A在圆上,∵直线x=1过点A且为圆的切线,又l斜率存在,∴l与圆一定相交,故选C.
2.(2020·天津一中高二期末)若直线x-y=2被圆(x-a)2+y2=4所截得的弦长为2,则实数a的值为( )
A.0或4 B.0或3
C.-2或6 D.-1或
【答案】A
【解析】由圆的方程,可知圆心坐标为(a,0),半径r=2.又直线被圆截得的弦长为2,所以圆心到直线的距离d==.又d=,所以|a-2|=2,解得a=4或a=0.故选A.
3.(2020·江西南昌二中高二月考)由直线y=x+1上的一点向圆(x-3)2+y2=1引切线,则切线长的最小值为( )
A.1 B.2
C. D.3
【答案】C
【解析】因为切线长的最小值是当直线y=x+1上的点与圆心距离最小时取得,圆心(3,0)到直线y=x+1的距离为d==2,圆的半径为1,所以切线长的最小值为==,故选C.
4.(多选) (2020·山东潍坊第一中学高二月考)与圆C:x2+y2-4x+2=0相切,且在x,y轴上的截距相等的直线方程为( )
A.x+y=0 B.x-y=0
C.x=0 D.x+y=4
【答案】ABD
【解析】圆C的方程可化为(x-2)2+y2=2.可分为两种情况讨论:
(1)直线在x,y轴上的截距均为0,易知直线斜率必存在,设直线方程为y=kx,则=,解得k=±1;
(2)直线在x,y轴上的截距均不为0,则可设直线方程为+=1(a≠0),即x+y-a=0(a≠0),则=,解得a=4(a=0舍去).
5.(2020·山东省郓城第一中学高二月考)一辆卡车宽1.6米,要经过一个半径为3.6米的半圆形隧道,则这辆卡车的平顶车蓬蓬顶距地面的高度不得超过( )
A.1.4米 B.3.5米
C.3.6米 D.2米
【答案】B
【解析】建立如图所示的平面直角坐标系.如图设蓬顶距地面高度为h,则A(0.8,h-3.6)所在圆的方程为: x2+(y+3.6)2=3.62,把A(0.8,h-3.6)代入得0.82+h2=3.62.∴h=4≈3.5(米).
6.(2020·五莲县教学研究室高二期中)若点P(1,2)在以坐标原点为圆心的圆上,则该圆在点P处的切线方程为________.
【答案】x+2y-5=0
【解析】设切线斜率为k,则由已知得: k·kOP=-1.
∴k=-.∴切线方程为x+2y-5=0.
7.(2020·重庆市万州沙河中学高二月考)已知圆C的圆心是直线x-y+1=0与x轴的交点,且圆C与直线x+y+3=0相切,则圆C的方程为____________________.
【答案】 (x+1)2+y2=2
【解析】令y=0得x=-1,所以直线x-y+1=0与x轴的交点为(-1,0).因为直线x+y+3=0与圆相切,
所以圆心到直线的距离等于半径,
即r==,
所以圆C的方程为(x+1)2+y2=2.
8.(2020·江苏省南通中学高二期中)点M,N在圆x2+y2+kx+2y+4=0上,且点M,N关于直线x-y+1=0对称,则该圆的半径是________.
【答案】1
【解析】由题知,直线x-y+1=0过圆心,
即-+1+1=0,∴k=4.∴r==1.
9.(2020·苏州市相城区陆慕高级中学高二月考)已知直线方程mx-y-m-1=0,圆的方程x2+y2-4x-2y+1=0.当m为何值时,圆与直线:
(1)有两个公共点;
(2)只有一个公共点;
(3)没有公共点.
【解析】法一:将直线mx-y-m-1=0代入圆的方程化简整理得,
(1+m2)x2-2(m2+2m+2)x+m2+4m+4=0.
则Δ=4m(3m+4).
(1)当Δ>0,即m>0或m<-时,直线与圆相交,即直线与圆有两个公共点;
(2)当Δ=0,即m=0或m=-时,直线与圆相切,即直线与圆只有一个公共点;
(3)当Δ<0,即-
即圆心为C(2,1),半径r=2.
圆心C(2,1)到直线mx-y-m-1=0的距离
d== .
(1)当d<2,即m>0或m<-时,直线与圆相交,即直线与圆有两个公共点;
(2)当d=2,即m=0或m=-时,直线与圆相切,即直线与圆只有一个公共点;
(3)当d>2,即-
(1)求圆A的方程;
(2)当|MN|=2时,求直线l的方程.
【解析】(1)设圆A的半径为r.∵圆A与直线l1:x+2y+7=0相切,∴r==2.
∴圆A的方程为(x+1)2+(y-2)2=20.
(2)①当直线l与x轴垂直时,直线l的方程为x=-2,
易得|MN|=2,符合题意;
②当直线l与x轴不垂直时,
设直线l的方程为y=k(x+2),即kx-y+2k=0.
取MN的中点Q,连接AQ,则AQ⊥MN.
∵|MN|=2,∴|AQ|==1,
∴=1,得k=,
∴直线l的方程为3x-4y+6=0.
综上,直线l的方程为x=-2或3x-4y+6=0.
11. (2020·运城市景胜中学高二期中)瑞士数学家欧拉(LeonhardEuler)1765年在其所著的《三角形的几何学》一书中提出:任意三角形的外心、重心、垂心在同一条直线上,后人称这条直线为欧拉线.已知的顶点,,其欧拉线方程为,则顶点的坐标可以是( )
A. B. C. D.
【答案】AD
【解析】设的垂直平分线为,
的外心为欧拉线方程为
与直线的交点为,
,①
由,,重心为,
代入欧拉线方程,得,②
由 ①②可得或 .故选:AD
12. (2020·宜宾市叙州区第一中学校高二月考)设有一组圆:().下列四个命题中真命题的是( )
A.存在一条定直线与所有的圆均相切
B.存在一条定直线与所有的圆均相交
C.存在一条定直线与所有的圆均不相交
D.所有的圆均不经过原点
【答案】BD
【解析】圆心为,半径为,
,,,,,圆与圆是内含关系,因此不可能有直线与这两个圆都相切,从而A错误;
易知圆心在直线上,此直线与所有圆都相交,B正确;
若取无穷大,则所有直线都与圆相交,C错;
将代入圆方程得,即,等式左边是奇数,右边是偶数,因此方程无整数解,即原点不在任一圆上,D正确.故选:BD.
13.(2020·四川邻水实验学校高二期中)过原点O作圆x2+y2-6x-8y+20=0的两条切线,设切点分别为P,Q,则线段PQ的长为________.
【答案】4
【解析】圆的方程化为标准方程为(x-3)2+(y-4)2=5,示意图如图所示.则圆心为O′(3,4),r=.切线长|OP|==2.
∴|PQ|=2·=2×=4.
14. (2020·福建厦门双十中学高二月考)已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的右上方.
(1)求圆C的方程;
(2)过点M(1,0)的直线与圆C交于A,B两点(A在x轴上方),问在x轴正半轴上是否存在定点N,使得x轴平分∠ANB?若存在,请求出点N的坐标;若不存在,请说明理由.
【解析】(1)设圆心C(a,0),则=2⇒a=0或a=-5(舍).所以圆C:x2+y2=4.
(2)当直线AB⊥x轴时,x轴平分∠ANB.
当直线AB的斜率存在时,设直线AB的方程为y=k(x-1),N(t,0),A(x1,y1),B(x2,y2),
由得,(k2+1)x2-2k2x+k2-4=0,
所以x1+x2=,x1x2=.若x轴平分∠ANB,则kAN=-kBN⇒+=0⇒+=0⇒2x1x2-(t+1)(x1+x2)+2t=0⇒-+2t=0⇒t=4,
所以当点N为(4,0)时,能使得∠ANM=∠BNM总成立.
15.(2020·湖北高二期中)在①圆经过,②圆心在直线上,③圆截轴所得弦长为8且圆心的坐标为整数;这三个条件中任选一个,补充在下面的问题中,进行求解.
已知圆经过点,且______;
(1)求圆的方程;
(2)已知直线经过点,直线与圆相交所得的弦长为8,求直线的方程.
【答案】B
【解析】选条件①,
(1)设圆的方程为,
依题意有,
解得,,,
所以圆的方程为,
即圆的标准方程为:.
(2)设圆心到直线的距离为,
则弦长,
当直线的斜率不存在时,,所以直线的斜率存在,
设其方程为,即,
,解得,,
所以所求直线的方程为或.
选条件②,
(1)设圆的方程为,
因为圆经过点,,且圆心在直线上
依题意有,
解得,,,
所以圆的方程为.
(2)设圆心到直线的距离为,
则弦长,
当直线的斜率不存在时,,所以直线的斜率存在,
设其方程为,即,
,解得,,
所以所求直线的方程为或.
选条件③,
设圆的方程为,
由圆经过点,,故,
又因为圆截轴所得弦长为8,
故方程的两个实数根的差的绝对值为.
所以,即
解方程组,
得,,或,,,
由于圆心的坐标为整数,
故圆的方程为
(2)设圆心到直线的距离为,
则弦长,
当直线的斜率不存在时,,所以直线的斜率存在,
设其方程为,即,
,解得,,
所以所求直线的方程为或.
相关资料
更多









