高中数学北师大版 (2019)选择性必修第一册2.2 空间向量的运算图片ppt课件

展开

这是一份高中数学北师大版 (2019)选择性必修第一册2.2 空间向量的运算图片ppt课件，共22页。PPT课件主要包含了内容索引，自主预习新知导学，合作探究释疑解惑，空间向量的夹角，图3-2-5，答案A，图3-2-6，两个向量的数量积，图3-2-7，图3-2-8等内容，欢迎下载使用。

(1)定义:已知两个非零向量a,b,如图3-2-5,在空间中任取一点O,作 =b,则 ∠AOB 叫作向量a与b的夹角,记作.通常规定 0≤≤π .在此规定下,两个向量的夹角被唯一确定,并且=.(2)当= 0 时,向量a与b方向相同;当= π 时,向量a与b方向相反;当= 时,称向量a,b互相垂直,记作a⊥b.规定:零向量与任意向量垂直.
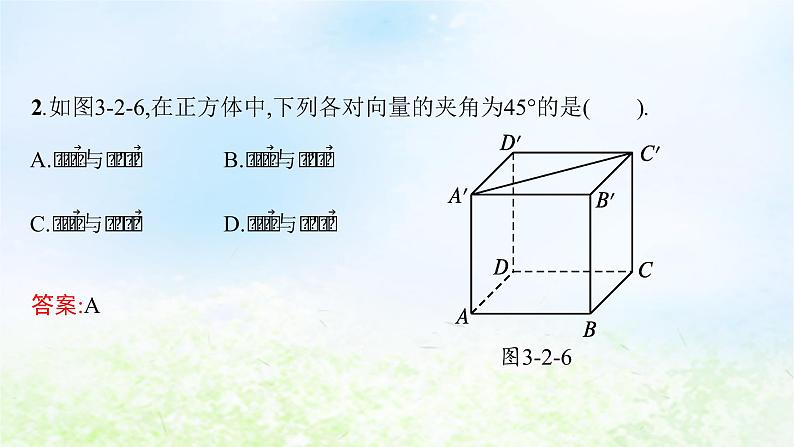
2.如图3-2-6,在正方体中,下列各对向量的夹角为45°的是(　　).
1.空间向量的数量积(1)定义:已知两个空间向量a,b,把 |a||b|cs 叫作a与b的数量积,记作a·b,即a·b=|a||b|cs.(2)与平面向量类似,空间向量的数量积也是一个实数,有如下性质:①cs= (a≠0,b≠0);③a⊥b⇔ a·b=0 .
(3)与平面向量类似,空间向量的数量积运算也满足如下运算律:①交换律:a·b=b·a;②分配律:a·(b+c)= a·b+a·c ;③(λa)·b=λ(a·b)(λ∈R).
2.已知|a|=2,|b|= ,=45°,则a·(2b-a)=(　　).A.0B.1C.-1D.解析:a·(2b-a)=2|a||b|cs 45°-|a|2=4-4=0.答案:A
三、投影向量与投影数量
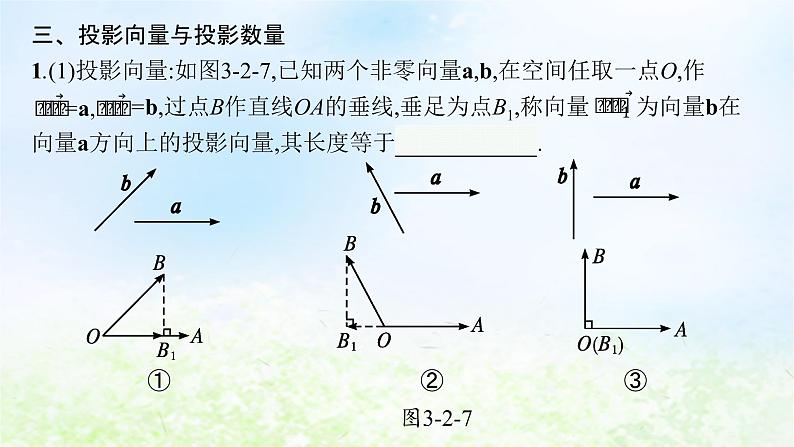
1.(1)投影向量:如图3-2-7,已知两个非零向量a,b,在空间任取一点O,作 =b,过点B作直线OA的垂线,垂足为点B1,称向量为向量b在向量a方向上的投影向量,其长度等于 ||b|cs| .
当为锐角时,|b|cs>0(如图3-2-7①);当为钝角时,|b|cs<0(如图3-2-7②);当= 时,|b|cs=0(如图3-2-7③).
(2)投影数量:称|b|cs为投影向量的数量,也称为向量b在向量a方向上的投影数量.向量b在向量a方向上的投影数量为|b|·cs= ,其中a0表示与向量a(a≠0)同方向的单位向量.
2.已知|a|=8,|b|=4,=120°,则向量b在a方向上的投影数量为(　　).A.4B.-4C.2D.-2解析:向量b在a方向上的投影数量为|b|cs=4×cs 120°=-2.答案:D
【例1】如图3-2-8,已知空间四边形ABCD的每条边和对角线的长都等于3,E,F分别是AB,AD的中点,试计算:
1.空间向量运算的两种方法(1)利用定义:利用a·b=|a||b|cs并结合运算律进行计算.(2)利用图形:计算两个向量的数量积,可先将各向量移到同一顶点,利用图形寻找夹角,再代入数量积公式进行运算.2.在几何体中求空间向量数量积的步骤(1)首先将各向量分解成已知模和夹角的向量的组合形式.(2)利用向量的运算律将数量积展开,转化为已知模和夹角的向量的数量积.(3)代入a·b=|a||b|cs求解.
【例2】如图3-2-9,已知正四面体OABC的棱长为1,E,F分别是AB,OC的中点,求向量成角的余弦值.
如图3-2-10,在空间四边形OACB中,OB=OC,AB=AC,求证:OA⊥BC.
证明:因为OB=OC,AB=AC,OA=OA,所以△OAC≌△OAB,所以∠AOC=∠AOB.
求两个向量的夹角,可以把两个向量的起点平移到同一点,从而转化为求平面角的大小;也可以利用向量的数量积定义a·b=|a||b|cs,求出cs= 的值,然后确定的大小.

相关课件更多