数学选择性必修 第一册3.1 空间向量基本定理说课课件ppt

这是一份数学选择性必修 第一册3.1 空间向量基本定理说课课件ppt，共22页。PPT课件主要包含了课标要求，素养要求等内容，欢迎下载使用。

3.2 空间向量运算的坐标表示及应用 第1课时 空间向量运算的坐标表示、空间向量平行（共线）和垂直的条件
空间向量基本定理 如果向量a,b,c是空间三个不共面的向量，p是空间任意一个向量,那么存在唯一的三元有序实数组(x,y,z),使得
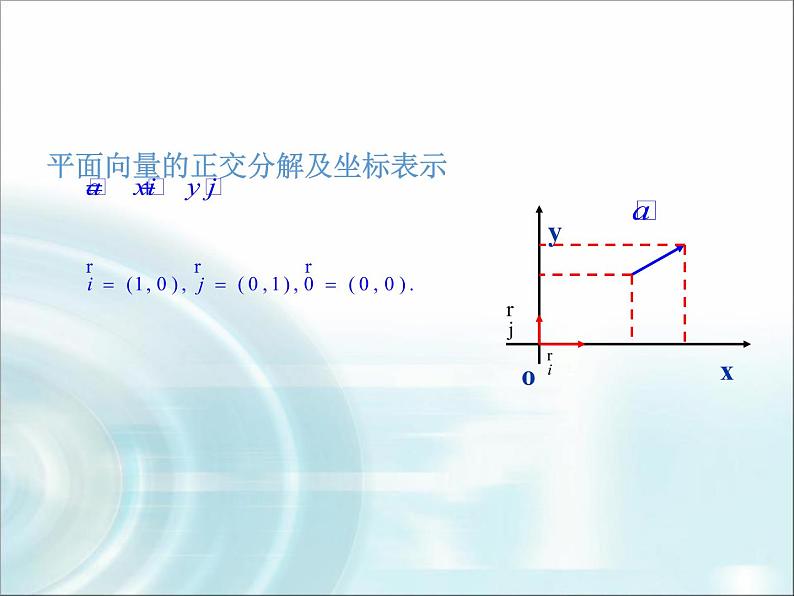
平面向量的正交分解及坐标表示
平面向量运算的坐标表示：
空间向量运算的坐标表示又是怎样的呢 ?
类比是我们探究规律的重要方法
1.理解标准正交基和坐标向量.2.掌握有向线段空间向量的坐标表示，能在适当的坐标系中写出向量的坐标.3.掌握空间向量的坐标运算法则.4.空间向量平行和垂直的条件.
1.掌握空间向量的坐标运算规律,培养数学运算素养.2.会判断两个向量的共线或垂直,培养数学抽象素养.
探究点1 空间向量的基底和基向量
在空间直角坐标系O-xyz中，分别沿x轴、y轴、z轴正方向作单位向量i,j,k,这三个互相垂直的单位向量就构成空间向量的一组基{i,j,k,},这组基叫作标准正交基. 根据空间向量基本定理,对于任意一个向量p,都存在唯一的三元有序实数组(x,y,z)，使得 p=xi+yj+zk.
任意给出一个三元有序实数组(x,y,z),也可找到唯一的一个向量p=xi+yj+zk与之对应. 就在空间向量与三元有序实数组之间建立了 一一对应的关系,把三元有序实数组(x,y,z)叫作向量p在标准正交基{i,j,k,}下的坐标，记作
单位向量i,j,k都叫作坐标向量. xi,yj,zk实际上分别是向量p在i,j,k方向上所作的投影向量, x,y,z分别是向量p在i,j,k方向上所作投影向量的数量.
探究点2 向量在空间直角坐标系中的坐标
设向量a=（x1,y1,z1），b=（x2,y2,z2），由空间向量的运算法则，得：
（1）a+b =（x1+x2，y1+y2，z1+z2）；（2）a-b =（x1-x2，y1-y2，z1-z2）;（3）λa =（λx1,λy1,λz1），λ∈R;（4）a·b =x1x2+y1y2+z1z2.
探究点3 空间向量的运算法则
例2 已知向量a=(-l,-3,2)，b=(1,2,0),求：(1)2a；(2) (a+2b)·(-2a+b).
解 (1) 2a=2(-1,-3,2) = (-2,-6,4).(2)因为a+2b=(-1,-3,2)+2(1,2,0)= (-1,-3,2) + (2,4,0)= (1,1,2),-2a+b =-2( - 1,-3,2) + (1,2,0)=(2,6,-4) + (1,2,0)= (3,8,-4),所以(a+2b)·(-2a+b)= (l,l,2)·(3,8,-4)= 1×3 + 1×8+2×(-4) =3.
探究点4 空间向量平行(共线)和垂直的条件
当b≠0时，a∥b⇔∃λ∈R,使得a=λb.如果设向量a=（x1,y1,z1），b=（x2,y2,z2），那么当b≠0时, x1=λx2，a∥b⇔∃λ∈R,使得， y1=λy2， z1=λz2,
1.点A(1,-2,11),B(4,2,3),C(6,-1,4)，则三角形ABC的形状是( )
A. 等腰三角形     B.等边三角形 C. 直角三角形      D. 等腰直角三角形