高中数学高考第16讲 导数的应用——导数与函数的极值、最值（学生版）

这是一份高中数学高考第16讲 导数的应用——导数与函数的极值、最值（学生版），共9页。试卷主要包含了函数的极值，函数的最值等内容，欢迎下载使用。
思维导图
知识梳理
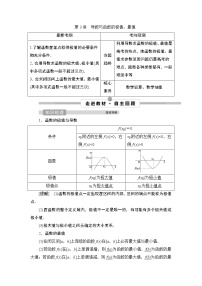
1．函数的极值
(1)函数的极小值：
函数y＝f(x)在点x＝a的函数值f(a)比它在点x＝a附近其他点的函数值都小，f′(a)＝0；而且在点x＝a附近的左侧f′(x)＜0，右侧f′(x)＞0，则点a叫做函数y＝f(x)的极小值点，f(a)叫做函数y＝f(x)的极小值．
(2)函数的极大值：
函数y＝f(x)在点x＝b的函数值f(b)比它在点x＝b附近其他点的函数值都大，f′(b)＝0；而且在点x＝b附近的左侧f′(x)＞0，右侧f′(x)＜0，则点b叫做函数y＝f(x)的极大值点，f(b)叫做函数y＝f(x)的极大值．
2．函数的最值
(1)在闭区间[a，b]上连续的函数f(x)在[a，b]上必有最大值与最小值．
(2)若函数f(x)在[a，b]上单调递增，则f(a)为函数的最小值，f(b)为函数的最大值；若函数f(x)在[a，b]上单调递减，则f(a)为函数的最大值，f(b)为函数的最小值．
题型归纳
题型1 利用导数解决函数的极值问题——根据函数图象判断函数极值
【例1-1】（2020春•宜宾期末）如图是函数的导函数的图象，则函数的极大值点的个数为
A．3B．2C．1D．0
【例1-2】（2019秋•未央区校级期末）函数的图象如图所示，则关于函数的说法正确的是
A．函数有3个极值点
B．函数在区间上是增加的
C．函数在区间上是增加的
D．当时，函数取得极大值
【跟踪训练1-1】（2019秋•临渭区期末）已知函数的导函数的图象如图所示，则关于的结论正确的是
A．在区间上为减函数
B．在处取得极小值
C．在区间，上为增函数
D．在处取得极大值
【跟踪训练1-2】（2019秋•咸阳期末）已知函数的导函数的图象如图，则下列叙述正确的是
A．函数在上单调递减
B．函数在处取得极大值
C．函数在处取得极值
D．函数只有一个极值点
【名师指导】
由图象判断函数y＝f(x)的极值，要抓住两点：(1)由y＝f′(x)的图象与x轴的交点，可得函数 y＝f(x)的可能极值点；(2)由导函数y＝f′(x)的图象可以看出y＝f′(x)的值的正负，从而可得函数y＝f(x)的单调性．两者结合可得极值点．
题型2 利用导数解决函数的极值问题——已知函数求极值或极值点
【例2-1】（2020春•顺义区期末）已知函数，则的极大值点为
A．B．C．D．
【例2-2】（2020春•海淀区校级期末）函数的一个极小值点为
A．B．C．D．
【跟踪训练2-1】（2020春•乐山期中）函数的极小值是
A．4B．2C．D．
【跟踪训练2-2】（2020春•龙岩期末）函数的极大值为 ．
【名师指导】
求函数的极值或极值点的步骤
(1)求导数f′(x)，不要忘记函数f(x)的定义域；
(2)求方程f′(x)＝0的根；
(3)检查在方程的根的左右两侧f′(x)的符号，确定极值点或函数的极值．
题型3 利用导数解决函数的极值问题——已知函数的极值点或极值求参数的值或范围
【例3-1】（2020春•赤峰期末）若函数存在极值点，则实数的取值范围是
A．B．，C．D．，
【例3-2】（2020春•荆州期末）若当时，函数有两个极值点，则实数的取值范围是
A．，B．C．D．
【跟踪训练3-1】（2020春•潍坊期末）已知时，函数取得极大值，则
A．B．C．4D．2
【跟踪训练3-2】（2020春•南阳期末）已知函数有且仅有一个极值点，则实数的取值范围是 ．
【跟踪训练3-3】（2020•临川区校级一模）已知函数为自然对数的底数）有两个极值点，则实数的取值范围是 ．
【名师指导】
已知函数极值点或极值求参数的两个要领
(1)列式：根据极值点处导数为0和极值这两个条件列方程组，利用待定系数法求解．
(2)验证：因为导数值等于零不是此点为极值点的充要条件，所以利用待定系数法求解后必须验证根的合理性．
题型4 利用导数求函数的最值
【例4-1】（2020春•克什克腾旗校级月考）（文科普班）已知，若，求函数的最小值．
【例4-2】（2020春•徐州期中）已知函数．
（1）求函数的单调区间；
（2）求函数在，上的最大值和最小值．
【跟踪训练4-1】（2020春•十堰期末）函数在，上的最大值为2，则的值为
A．B．2C．5D．
【跟踪训练4-2】（2020春•内江期末）函数在，上的
A．最小值为0，最大值为B．最小值为0，最大值为
C．最小值为1，最大值为D．最小值为1，最大值为
【跟踪训练4-3】（2020春•沭阳县期中）已知函数，且（1）．
（1）求的值；
（2）求函数在区间，上的最大值．
【名师指导】
导数法求给定区间上函数的最值问题的一般步骤
(1)求函数f(x)的导数f′(x)；
(2)求f(x)在给定区间上的单调性和极值；
(3)求f(x)在给定区间上的端点值；
(4)将f(x)的各极值与f(x)的端点值进行比较，确定f(x)的最大值与最小值；
(5)反思回顾，查看关键点，易错点和解题规范．
题型5 利用导数求解函数极值和最值的综合问题
【例5-1】（2020春•朝阳区期末）已知函数，
（Ⅰ）若，求证：当，时，恒成立；
（Ⅱ）当时，求在区间，上的最大值和最小值；
（Ⅲ）若函数存在极大值和极小值，且极大值和极小值的差不超过4，求的取值范围．
【跟踪训练5-1】（2020春•贵池区校级期中）已知，．
（1）若在处取极值，求在点处切线方程；
（2）若函数在区间，最小值为，求．
【名师指导】
解决函数极值、最值综合问题的策略
(1)求极值、最值时，要求步骤规范，含参数时，要讨论参数的大小．
(2)求函数最值时，不可想当然地认为极值点就是最值点，要通过比较才能下结论．
(3)函数在给定闭区间上存在极值，一般要将极值与端点值进行比较才能确定最值．