陕西省宝鸡市2023年七年级下学期期中数学试卷【含答案】

这是一份陕西省宝鸡市2023年七年级下学期期中数学试卷【含答案】，共8页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1．下列计算正确的是（ ）
A．a2+a3＝a5B．3a2•a3＝3a6
C．（﹣a2）3•a2＝﹣a12D．（﹣a3）2＝a6
2．若∠1与∠2互补，则∠1+∠2＝（ ）
A．90°B．100°C．180°D．360°
3．用简便方法计算，将99×101变形正确的是（ ）
A．B．
C．D．
4．如图，把一块三角板的 角的顶点放在直尺的一边上，若 ，则 的度数为（ ）
A．B．C．D．
5．如图，AB和CD相交于点O，则下列结论正确的是（ ）
A．∠1=∠2B．∠2=∠3C．∠3=∠4D．∠1=∠5
6．已知（x-m）（x+n）=x2-3x-4，则m-n的值为( )
A．1B．-3C．-2D．3
7．小丽早上步行去车站然后坐车去学校，下列能近似的刻画她离学校的距离随时间变化的大致图象是（ ）
A．B．
C．D．
8．如下图，在下列条件中，能判定AB//CD的是（ ）
A．∠1=∠3B．∠2=∠3C．∠1=∠4D．∠3=∠4
二、填空题
9．计算： .
10．按如图所示的运算程序，输入一个有理数x，便可输出一个相应的有理数y，写出y与x之间的关系式： ．
11．已知x2+y2＝10，xy＝3，则x+y＝ .
12．如图，射线OC的端点O在直线AB上，于点O，且OE平分，OF平分，若，则 ．
13．某社区组织老年人参加太极拳比赛，由于比赛场地的原因，要把每边 人的方队一边增加 人，另一边减少 人，实际参加比赛的人比原来 人
三、解答题
14．计算：（x+2）（x﹣3）+（x﹣1）2．
15．先化简，再求值：
（x﹣2y）（x+2y）+（x+y）（x﹣4y），其中x＝1，y＝﹣2.
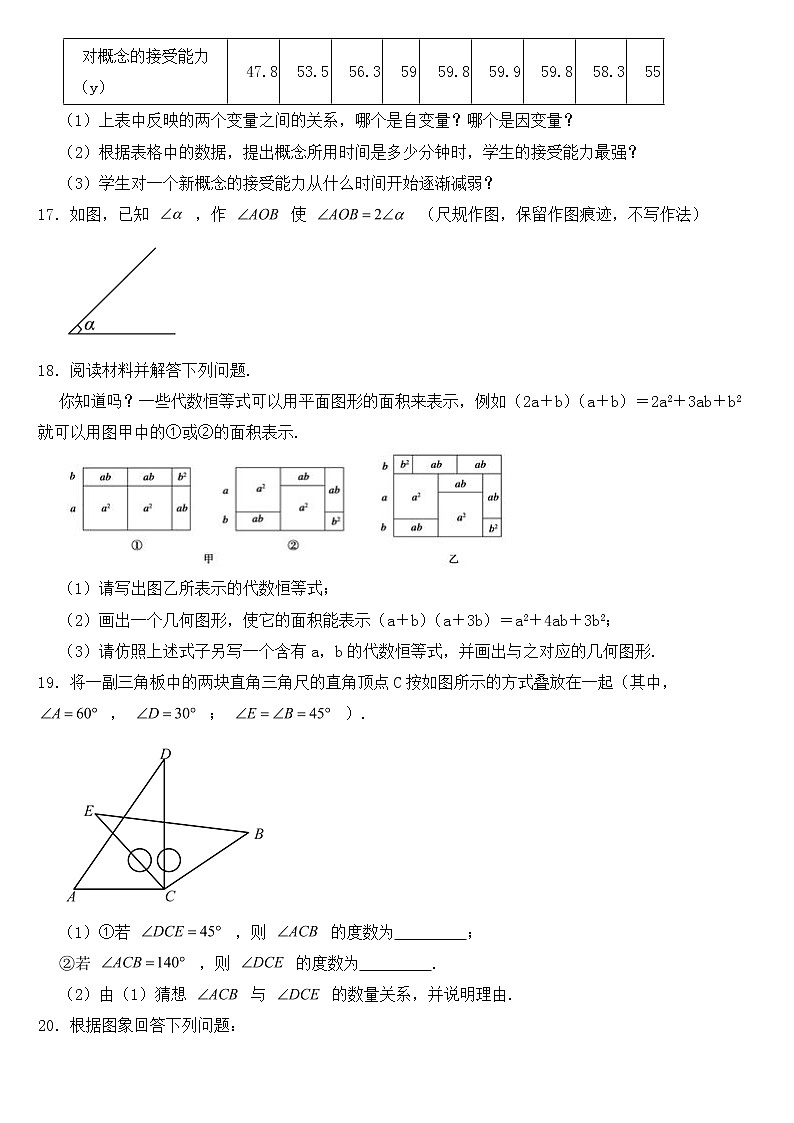
16．根据心理学家研究发现，学生对一个新概念的接受能力y与提出概念所用的时间x（分钟）之间有如表所示的关系：
（1）上表中反映的两个变量之间的关系，哪个是自变量？哪个是因变量？
（2）根据表格中的数据，提出概念所用时间是多少分钟时，学生的接受能力最强？
（3）学生对一个新概念的接受能力从什么时间开始逐渐减弱？
17．如图，已知 ，作 使 （尺规作图，保留作图痕迹，不写作法）
18．阅读材料并解答下列问题.
你知道吗？一些代数恒等式可以用平面图形的面积来表示，例如（2a＋b）（a＋b）＝2a2＋3ab＋b2就可以用图甲中的①或②的面积表示.
（1）请写出图乙所表示的代数恒等式；
（2）画出一个几何图形，使它的面积能表示（a＋b）（a＋3b）＝a2＋4ab＋3b2；
（3）请仿照上述式子另写一个含有a，b的代数恒等式，并画出与之对应的几何图形.
19．将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起（其中， ， ； ）.
（1）①若 ，则 的度数为 ；
②若 ，则 的度数为 .
（2）由（1）猜想 与 的数量关系，并说明理由.
20．根据图象回答下列问题：
（1）上图反映了哪两个变量之间的关系？
（2）点A、B分别表示什么？
（3）说一说速度是怎样随时间变化而变化的？
（4）请写出一个实际情景，大致符合上图的关系.
21．点 在直线 上， 为射线， ．
（1）如图（1），求 的度数；
（2）如图（2），点 在直线 上方， 与 互余， 平分 ，求 的度数．
22．若我们规定三角“ ”表示为：abc；方框“ ”表示为：（xm＋yn）.例如： ＝1×19×3÷（24＋31）＝3.请根据这个规定解答下列问题：
（1）计算： ＝ ；
（2）代数式 为完全平方式，求k的值.
23．如图，P是∠AOB的OB边上的一点，点A、O、P都在格点上，在方格纸上按要求画图，并标注相应的字母.
（1）过点P画OB的垂线，交OA于点C；过点P画OA的垂线，垂足为D；并完成填空：
①线段 的长度表示点P到直线OA的距离；
②PC OC（填“＞”、“＜”或“＝”）
（2）过点A画OB的平行线AE.
24．已知，如图，EF⊥AC于F，DB⊥AC于M，∠1=∠2，∠3=∠C，求证：AB∥MN．
25．弹簧挂上物体后会伸长，已知一弹簧的长度（cm）与所挂物体的质量（kg）之间的关系如表所示.
（1）当物体的质量为2kg时，弹簧的长度是多少？
（2）当物体的质量逐渐增加时，弹簧的长度怎样变化？
（3）如果物体的质量为xkg，弹簧的长度为ycm，根据上表写出y与x的关系式；
（4）当物体的质量为2.5kg时，根据（3）的关系式，求弹簧的长度.
26．如图①②， 的两边分别平行.
（1）在图①中， 与 有什么数量关系？为什么？
（2）在图②中， 与 有什么数量关系？为什么？
（3）由（1）（2）你能得出什么结论？用一句话概括你得到的结论.
答案
1．D
2．C
3．C
4．B
5．A
6．D
7．D
8．C
9．
10．y＝5x＋6
11．±4
12．60°
13．少4
14．解：原式=x2-3x+2x-6+x2-2x+1
=2x2-3x-5．
15．解：原式＝x2﹣4y2+x2﹣4xy+xy﹣4y2
＝2x2﹣3xy﹣8y2，
当x＝1，y＝﹣2时，
原式＝2×12﹣3×1×（﹣2）﹣8×（﹣2）2
＝2+6﹣32
＝﹣24.
16．（1）解：表格中反映的是：提出概念所用时间与对概念的接受能力这两个变量，其中“提出概念所用时间”是自变量，“对概念的接受能力”为因变量；
（2）解：根据表格中的数据，提出概念所用时间是13分钟时，学生的接受能力最强达到59.9；
（3）解：学生对一个新概念的接受能力从第13分钟以后开始逐渐减弱.
17．解：如图，先作∠AOC=∠α，然后在其外部再作∠BOC=∠α，则可得∠AOB=2∠α，如图所示，∠AOB即为所求.
18．（1）解：（a＋2b）（2a＋b）＝2a2＋5ab＋2b2
（2）解：画法不唯一，如图所示：
（3）解：答案不唯一，例如：（a＋b）（a＋2b）＝a2＋3ab＋2b2可以用下图表示：
19．（1）；
（2）解： .
理由如下：
∵ ， ，∴ .
∵ ， ，
∴∴ .
20．（1）解：由图象的横坐标和纵坐标的的轴标签可得，该图象反映速度与时间的关系；
（2）解：A点表示当时间过了6分钟后，速度为60千米/时，B点表示当时间为18分钟时，速度为0千米/时；
（3）解：当时间在0~6分钟时，速度随时间的增加而从0千米/时增大到60千米/时，当时间在6~12分钟时，速度保持60千米/时不变，12到18分钟时，速度从60千米/时降到千米/时0；
（4）解：某人开车去上班，出发时汽车加速，6分钟内从0千米/时增大到60千米/时，之后保持该速度行驶了6分钟，快到公司了，此时汽车开始减速，6分钟后到达公司，停车.
21．（1）解：设∠BOC=α，则∠AOC=4α，
∵∠BOC+∠AOC=180°，∴α+4α=180°，∴α=36°，∴∠AOC=144°；
（2）解：∵∠AOD与∠BOC互余， ∴∠AOD=90°-∠BOC=90°-36°=54°，
∠COD=180°-∠AOD-∠BOC=180°-54°-36°=90°，
∵OE平分∠COD，∴∠DOE= ∠COD= ×90°=45°，∴∠AOE=∠DOE+∠AOD=45°+54°=99°．
22．（1）
（2）解：依据题意，
有：原式= ；
∵代数式 为完全平方式，
∴原式= ，
∴将 展开，比较等号两边同类项系数可得2k＝±6，
解得k＝±3.
23．（1）PD；<
（2）解：如图，直线AE即为所求作.
24．证明：∵EF⊥AC，DB⊥AC，∴EF∥DM，∴∠2=∠CDM，
∵∠1=∠2，∴∠1=∠CDM，∴MN∥CD，∴∠C=∠AMN，
∵∠3=∠C，∴∠3=∠AMN，∴AB∥MN．
25．（1）解：通过表格可知，弹簧的长度由原来的12cm变为13cm；
（2）解：由表格中的数据可知，弹簧的长度随所挂物体的重量的增加而增加，并且每增加1千克的重量，长度增加0.5cm，；
（3）解：由表中的数据可知，
x=0时即没有挂重物时，弹簧的原长度y=12，并且每增加1千克的重量，长度增加0.5cm，即弹簧的总长度等于弹簧的原长度加上因挂有重物而增加的长度，
则弹簧总长y（cm）与所挂重物x（kg）之间的函数关系式为：y=0.5x+12；
（4）解：利用（3）中的关系式， 将x=2.5代入关系式，得y=12+0.5×2.5=13.25（cm）.
26．（1）解：∠B=∠E
理由：∵BA∥EF，BC∥DE，∴∠B=∠EOC，∠EOC=∠E，∴∠B=∠E；
（2）解：∠B+∠E=180°
理由：∵BA∥ED，BC∥EF，∴∠B=∠DOC，∠BOE+∠E=180°，
∵∠DOC=∠BOE，∴∠B+∠E=180°；
（3）如果两个角的两边分别平行，那么这两个角相等或互补. 提出概念所用时间（x）
2
5
7
10
12
13
14
17
20
对概念的接受能力（y）
47.8
53.5
56.3
59
59.8
59.9
59.8
58.3
55
所挂物体的质量
0
1
2
3
4
5
6
7
弹簧的长度
12
12.5
13
13.5
14
14.5
15
15.5