2023年浙江省杭州市中考数学模拟卷六（含答案）

这是一份2023年浙江省杭州市中考数学模拟卷六（含答案），共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（本大题有10小题，每小题3分，共30分）
下面每小题给出的四个选项中，只有一个是正确的.
1．某市2022年元旦的最高气温为6℃，最低气温为﹣4℃，那么这天的最高气温比最低气温高（ ）
A．﹣10℃B．﹣2℃C．2℃D．10℃
2．神舟十五号载人飞船于2022年11月29日成功发射，载人飞船与空间站组合体对接后，在距离地球表面约430000米左右的轨道上运行.430000米用科学记数法表示是（ ）．
A．4.3×103米B．4.3×105米C．43×104米D．0.43×104米
3．若m＞n，则下列不等式正确的是（ ）
A．m－2＜n－2B．am＞anC．－8m＞－8nD．m7>n7
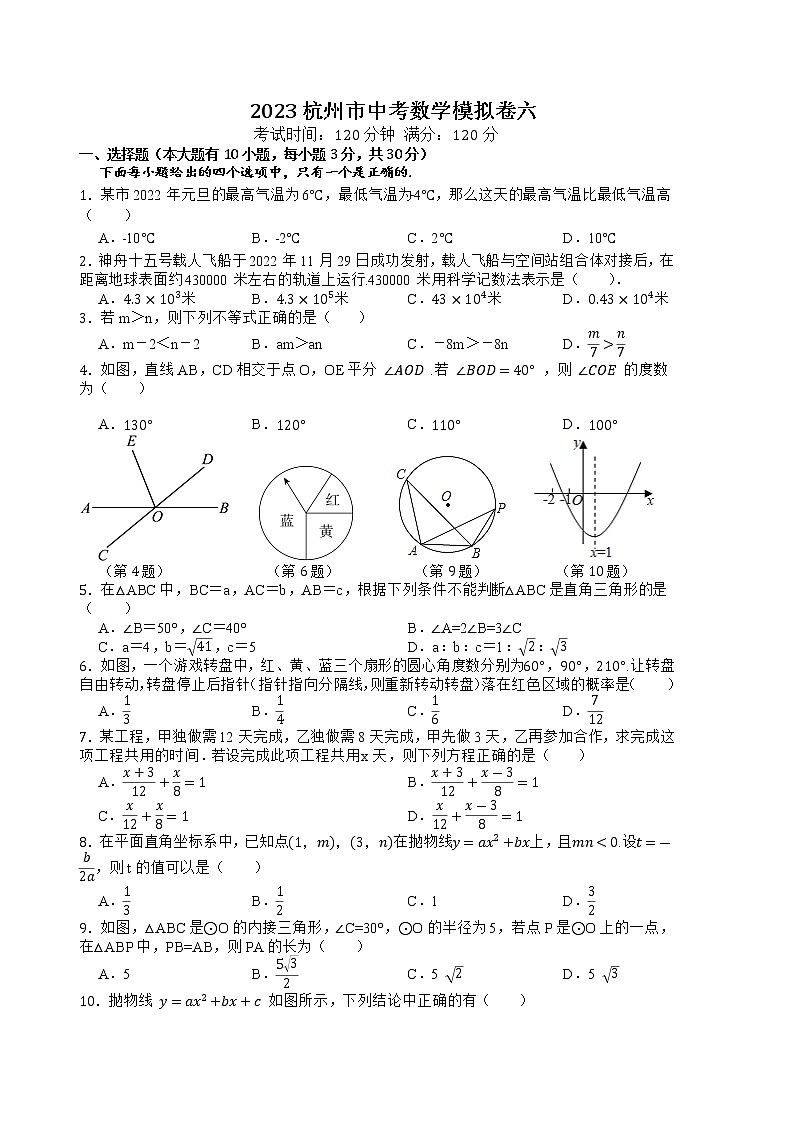
4．如图，直线AB，CD相交于点O，OE平分 ∠AOD .若 ∠BOD=40° ，则 ∠COE 的度数为（ ）
A．130°B．120°C．110°D．100°

（第4题） （第6题） （第9题） （第10题）
5．在△ABC中，BC＝a，AC＝b，AB＝c，根据下列条件不能判断△ABC是直角三角形的是（ ）
A．∠B＝50°，∠C＝40°B．∠A=2∠B=3∠C
C．a＝4，b＝41，c＝5D．a：b：c＝1：2：3
6．如图，一个游戏转盘中，红、黄、蓝三个扇形的圆心角度数分别为60°，90°，210°.让转盘自由转动，转盘停止后指针（指针指向分隔线，则重新转动转盘）落在红色区域的概率是（ ）
A．13B．14C．16D．712
7．某工程，甲独做需12天完成，乙独做需8天完成，甲先做3天，乙再参加合作，求完成这项工程共用的时间．若设完成此项工程共用x天，则下列方程正确的是（ ）
A．x+312+x8=1B．x+312+x-38=1
C．x12+x8=1D．x12+x-38=1
8．在平面直角坐标系中，已知点(1，m)，(3，n)在抛物线y=ax2+bx上，且mn<0.设t=-b2a，则t的值可以是（ ）
A．13B．12C．1D．32
9．如图，△ABC是⊙O的内接三角形，∠C=30°，⊙O的半径为5，若点P是⊙O上的一点，在△ABP中，PB=AB，则PA的长为（ ）
A．5B．532C．5 2D．5 3
10．抛物线 y=ax2+bx+c 如图所示，下列结论中正确的有（ ）
①abc>0 ； ②b2-4ac<0 ； ③9a+3b+c<0 ； ④(a+c)2A．1个B．2个C．3个D．4个
二、填空题（本大题有6小题，每小题4分，共24分）
要注意认真看清题目的条件和要填写的内容，尽量完整地填写答案.
11．cs45°=
12．若x－3y＝3，则代数式2x－6y＋5的值为 ．
13．已知关于 x ， y 的二元一次方程组 mx-y=1,y=nx 的解是 x=1,y=2 则直线 y=mx-1 与直线 y=nx 的交点坐标是 ；
14．如图，OC平分∠AOB，P是边OA上一点，以点P为圆心、大于点P到OB的距离为半径作弧，交OB于点E、F，再分别以点E、F为圆心，大于12EF的长为半径作弧，两弧交于点D．作直线PD分别交OC、OB于点G、Q．若sin∠AOB＝32，OP＝43，则△OPG的面积为 ．

（第14题） （第15题） （第16题）
15．如图，P为△ABC边BC上的一点，且PC＝2PB，已知∠ABC＝45°，∠APC＝60°，则∠ACB的度数是 °.
16．如图，在正方形ABCD中， AB=42 ，对角线 AC，BD 相交于点O.点E是对角线AC上一点，连接BE，过点E作 EF⊥BE ，分别交 CD，BD 于点F、G，连接BF，交AC于点H，将 △EFH 沿EF翻折，点H的对应点 H' 恰好落在BD上，得到 △EFH' 若点F为CD的中点，则 △EGH' 的周长是 .
三、解答题（本题有8小题，第17题6分，第18、19题每题8分，第20、21题10分，第22、23题12分，共66分）
解答应写出文字说明，证明过程或推演步骤.
17．
（1）计算： 12+(2014-π)0-4cs30° ；
（2）先化简，再求值： (x+1-2xx)÷2x-2x ，其中 x=2+1 .
18．某校在七、八年级举行了“食品安全知识测试”比赛，从七、八年级各随机抽取了10名学生的比赛成绩（百分制），测试成绩整理、描述和分析如下：（成绩得分用 x 表示，共分成四组： A ． 80≤x<85 ， B ． 85≤x<90 ， C ． 90≤x<95 ， D ． 95≤x<100 ）
七年级10名学生的成绩数据是：96，83，96，87，99，96，90，100，89，84．
八年级10名学生成绩数据中，在 C 组中的是：94，90，92．
七，八年级抽取的学生竞赛成绩统计表
八年级抽取的学生成绩扇形统计图
根据以上信息，解答下列问题：
（1）这次比赛中哪个年级成绩更稳定，并说明理由；
（2）求出统计图中 a 的值以及表格中 b 的值；
（3）该校七年级共860人参加了此次比赛，估计参加此次比赛成绩优秀（ x≥90 ）的七年级学生人数是多少？
19．如图，在△ABC中，边AB绕点B顺时针旋转60°与BC重合，点D、E分别在边BC、AC上，∠ADE＝60°．
（1）求证：△ABD∽△DCE；
（2）若BD＝1，CE＝23，求△ABC的边长．
20．如图，一次函数y=k1x+b的图像与x轴，y轴分别交于A，B两点，与反比例函数y=k2x的图像分别交于C，D两点，已知点C坐标是(3，6)，AB=BC.
（1）求一次函数y=k1x+b与反比例函数y=k2x的解析式：
（2）直接写出不等式k1x+b（3）求△COD的面积.
21．如图，点E是正方形ABCD的边AB上的一点，延长BC到F使AE=CF，连接DE、DF.
（1）能通过旋转△DAE得到△DCF吗？说明理由.
（2）连接EF，过D作DM垂直EF于M，交BC于N，若BN=3，CN=2，求AE的长.
22．在平面直角坐标系中，已知二次函数y＝﹣x2+2kx+k﹣1（k是常数）.
（1）当k＝﹣2时，求该二次函数图象与x轴的交点坐标；
（2）若该函数图象经过点（1，4），求该二次函数图象的顶点坐标；
（3）当0≤x≤1时，该函数有最大值4，求k的值.
23．如图，已知AC为⊙O的直径，连接AB，BC，OB，过点O作OE⊥AB于点E，点F是半径OC的中点，连接EF，BF.
（1）如图1，设⊙O的半径为2，若∠BAC＝30°，求线段EF的长.
（2）如图2，设BO交EF于点P，延长BO交⊙O于点D，连接DF.
①求证：PE＝PF；
②若DF＝EF，求∠BAC的度数.
答案与解析版
一、选择题（本大题有10小题，每小题3分，共30分）
下面每小题给出的四个选项中，只有一个是正确的.
1．某市2022年元旦的最高气温为6℃，最低气温为﹣4℃，那么这天的最高气温比最低气温高（ ）
A．﹣10℃B．﹣2℃C．2℃D．10℃
【答案】D
【解析】 这天的最高气温比最低气温高 ：6-（-4）=10℃.
故答案为：D.
2．神舟十五号载人飞船于2022年11月29日成功发射，载人飞船与空间站组合体对接后，在距离地球表面约430000米左右的轨道上运行.430000米用科学记数法表示是（ ）．
A．4.3×103米B．4.3×105米C．43×104米D．0.43×104米
【答案】B
【解析】430000米用科学记数法表示是4.3×105米；
故答案为：B．
3．若m＞n，则下列不等式正确的是（ ）
A．m－2＜n－2B．am＞anC．－8m＞－8nD．m7>n7
【答案】D
【解析】A、若m＞n，则m-2＞n-2，故此选项错误，不符合题意；
B、若m＞n，则当a＞0时，am＞an，故此选项错误，不符合题意；
C、若m＞n，则-8m＜-8n，故此选项错误，不符合题意；
D、若m＞n，则m7>n7，故此选项正确，符合题意.
故答案为：D.
4．如图，直线AB，CD相交于点O，OE平分 ∠AOD .若 ∠BOD=40° ，则 ∠COE 的度数为（ ）
A．130°B．120°C．110°D．100°
【答案】C
【解析】 ∵ ∠BOD=40° ，
∴∠AOD=180°-40°=140°，∠AOC=∠BOD=40°，
∵ OE平分 ∠AOD ，
∴∠AOE=12∠AOD=70°，
∴∠COE=∠AOC+∠AOE=110°.
故答案为：C.
5．在△ABC中，BC＝a，AC＝b，AB＝c，根据下列条件不能判断△ABC是直角三角形的是（ ）
A．∠B＝50°，∠C＝40°B．∠A=2∠B=3∠C
C．a＝4，b＝41，c＝5D．a：b：c＝1：2：3
【答案】B
【解析】A、∵∠B=50°，∠C=40°，∴∠A=180°-50°-40°=90°，故△ABC是直角三角形，此选项不符合题意；
B、∵∠A=2∠B=3∠C，
∴∠B=12∠A，∠C=13∠A，
∵∠A+∠B+∠C=180°，
∴∠A+12∠A+13∠A=180°，
解得∠A≈98°，故△ABC不是直角三角形，此选项符合题意；
C、∵a=4，b=41，c=5，∴a2+b2=16+25=c2=41，故△ABC是直角三角形，此选项不符合题意；
D、∵a∶b∶c=1∶2∶3，∴b=2a，c=3a，∴a2+b2=3a2=c2，故△ABC是直角三角形，此选项不符合题意.
故答案为：B.
6．如图，一个游戏转盘中，红、黄、蓝三个扇形的圆心角度数分别为60°，90°，210°.让转盘自由转动，转盘停止后指针（指针指向分隔线，则重新转动转盘）落在红色区域的概率是（ ）
A．13B．14C．16D．712
【答案】C
【解析】由题意可得，
P=60°πr2360°πr2=16，
故答案为：C.
7．某工程，甲独做需12天完成，乙独做需8天完成，甲先做3天，乙再参加合作，求完成这项工程共用的时间．若设完成此项工程共用x天，则下列方程正确的是（ ）
A．x+312+x8=1B．x+312+x-38=1
C．x12+x8=1D．x12+x-38=1
【答案】D
【解析】 设完成此项工程共用x天，则甲的工作量为x12，乙的工作量为x-38，
由题意得：x12+x-38=1.
故答案为：D.
8．在平面直角坐标系中，已知点(1，m)，(3，n)在抛物线y=ax2+bx上，且mn<0.设t=-b2a，则t的值可以是（ ）
A．13B．12C．1D．32
【答案】C
【解析】∵点(1，m)、(3，n)在抛物线上，
∴有：a+b=m9a+3b=n，解得a=n-3m6b=9m-n6，
∴t=-b2a=-9m-n62×n-3m6=n-9m2n-6m，
∵mn＜0，即mn≠0，
∴t=n-9m2n-6m=n-9mn2n-6mn=1-9mn2-6mn，
∴设S=mn，则有S＜0，
∴S=13×1-2t3-2t，
∵ S＜0，
∴1-2t3-2t＜0，
∴1-2t＜0＜3-2t，
∴即t的取值范围：12＜t＜32，
∴则t可以取1，
故答案为：C.
9．如图，△ABC是⊙O的内接三角形，∠C=30°，⊙O的半径为5，若点P是⊙O上的一点，在△ABP中，PB=AB，则PA的长为（ ）
A．5B．532C．5 2D．5 3
【答案】D
【解析】【解答】连接OA、OB、OP，
∵∠C=30°，
∴∠APB=∠C=30°，
∵PB=AB，
∴∠PAB=∠APB=30°
∴∠ABP=120°，
∵PB=AB，
∴OB⊥AP，AD=PD，
∴∠OBP=∠OBA=60°，
∵OB=OA，
∴△AOB是等边三角形，
∴AB=OA=5，
则Rt△PBD中，PD=cs30°•PB= 32 ×5= 532 ，
∴AP=2PD=5 3 ，
故答案为：D．
10．抛物线 y=ax2+bx+c 如图所示，下列结论中正确的有（ ）
①abc>0 ； ②b2-4ac<0 ； ③9a+3b+c<0 ； ④(a+c)2A．1个B．2个C．3个D．4个
【答案】C
【解析】 ∵ 抛物线开口向上、顶点在y轴右侧、抛物线与y轴交于负半轴，
∴a>0 ， b<0 ， c<0 ，
∴abc>0 ，故①正确；
∵ 抛物线与x轴有两个交点，
∴b2-4ac>0 ，故②错误；
∵ 抛物线对称轴为 x=1 ，
∴ 当 x=-1 和 x=3 时函数值相等，且 x=-1 时， y<0 ，
∴9a+3b+c<0 ，故③正确；
当 x=-1 时， a-b+c<0 ，
当 x=1 时， a+b+c<0 ，
∵(a+c)2-b2=(a-b+c)(a+b+c)>0 ，
∴(a+c)2∵ 当 x=1 时，函数值最小，
∴ 当 x=m(m≠1) 时， am2+bm+c>a+b+c ，即 a+b故答案为：C.
二、填空题（本大题有6小题，每小题4分，共24分）
要注意认真看清题目的条件和要填写的内容，尽量完整地填写答案.
11．cs45°=
【答案】22
【解析】cs45°=22，
故答案为：22．
12．若x－3y＝3，则代数式2x－6y＋5的值为 ．
【答案】11
【解析】∵ x－3y＝3 ，∴2x-6y=6，∴ 2x－6y＋5 =6+5=11.
故答案为：11.
13．已知关于 x ， y 的二元一次方程组 mx-y=1,y=nx 的解是 x=1,y=2 则直线 y=mx-1 与直线 y=nx 的交点坐标是 ；
【答案】（1,2）
【解析】由 mx-y=1y=nx 可得 y=mx-1y=nx ，它的解为 x=1y=2 ，
故直线 y=mx-1 与直线 y=nx 的交点坐标是（1,2），
故答案为：（1,2）.
14．如图，OC平分∠AOB，P是边OA上一点，以点P为圆心、大于点P到OB的距离为半径作弧，交OB于点E、F，再分别以点E、F为圆心，大于12EF的长为半径作弧，两弧交于点D．作直线PD分别交OC、OB于点G、Q．若sin∠AOB＝32，OP＝43，则△OPG的面积为 ．
【答案】43
【解析】过点G作MG⊥OA于点M，
由作法可知PQ⊥OB，
∴∠POQ=90°，
∴sin∠AOB=PQOP=32即PQ43=32，
∴∠AOB=60°，
∴∠OPQ=90°-60°=30°，
∴OQ=12OP=23；
∵OC平分∠AOB，MG⊥OA，PQ⊥OB
∴∠GOQ=12∠AOB=30°，GM=GQ，
∴tan∠GOQ=tan30°=GQOQ
∴33=GQ23
解之：GQ=GM=2，
∴S△OPG=12OP·GM=12×43×2=43.
故答案为：43
15．如图，P为△ABC边BC上的一点，且PC＝2PB，已知∠ABC＝45°，∠APC＝60°，则∠ACB的度数是 °.
【答案】75
【解析】过C作AP的垂线CD，垂足为点D.连接BD，
∵△PCD中，∠CDP＝90°，∠APC＝60°，
∴∠DCP＝90°－∠APC＝30°，
∴PC＝2PD，
∵PC＝2PB，
∴BP＝PD，
∴△BPD是等腰三角形，
∴∠BDP＝∠DBP，
∵∠BDP＋∠DBP＝∠APC＝60°，
∴∠BDP＝∠DBP＝30°，
∵∠ABP＝45°，
∴∠ABD＝∠ABP－∠DBP＝15°，
∵∠BAP＝∠APC﹣∠ABC＝60°﹣45°＝15°，
∴∠ABD＝∠BAD＝15°，
∴BD＝AD，
∵∠DBP＝30°，∠DCP＝30°，
∴BD＝DC，
∴△BDC是等腰三角形，
∵BD＝AD，
∴AD＝DC，
∵∠CDA＝90°，
∴△ADC是等腰直角三角形，
∴∠ACD＝45°，
∴∠ACB＝∠DCP+∠ACD＝75°.
故答案为：75.
16．如图，在正方形ABCD中， AB=42 ，对角线 AC，BD 相交于点O.点E是对角线AC上一点，连接BE，过点E作 EF⊥BE ，分别交 CD，BD 于点F、G，连接BF，交AC于点H，将 △EFH 沿EF翻折，点H的对应点 H' 恰好落在BD上，得到 △EFH' 若点F为CD的中点，则 △EGH' 的周长是 .
【答案】5+5
【解析】过点E作PQ∥AD交AB于点P，交DC于点Q，
∵AD∥PQ，
∴AP=DQ， ∠BPQ=∠CQE ，
∴BP=CQ，
∵∠ACD=45° ，
∴BP=CQ=EQ，
∵EF⊥BE，
∴∠PEB+∠FEQ=90°
∵∠PBE+∠PEB=90°
∴∠PBE=∠FEQ ，
在 △BPE 与 △EQF 中∠BPQ=∠FQEPB=EQ∠PBE=∠FEQ
∴△BPE ≌ △EQF ，
∴BE=EF，
又∵BC=AB=42 ，F为中点，
∴CF=22 ，
∴BF=BC2+CF2=210 ，
∴BE=EF=2102=25 ，
又∵BO=422=4 ，
∴EO=BE2-BO2=2 ，
∴AE=AO-EO=4-2=2，
∵AB // FC，
∴△ABH∽△CFH ，
∴ABCF=AHCH ，
∴4222=AHCH=21 ，
∵AC=2AB=8 ，
∴AH=23×8=163 ，
CH=13×8=83 ，
∴EH=AH-AE= 163-2=103 ，
∵∠BEO+∠FEO=90° ，
∠BEO+∠EBO=90° ，
∴∠FEO=∠EBO ，
又∵∠EOB=∠EOG=90° ，
∴△EOB∽△GOE
∴EGBE=OGOE=OEOB ，
EG25=OG2=24=12 ，
∴EG= 5 ，OG=1，
过点F作FM⊥AC 于点M，
∴FM=MC== FC2=2 ，
∴MH=CH-MC= 83-2=23 ，
作FN⊥OD于点N，
FN=DF2=2， ，
在Rt △FH'N 与Rt △FMH 中FH'=FHFN=FM
∴Rt △FH'N ≌Rt △FHM
∴H'N=MH=23 ，
∴ON=2，NG=1，
∴GH'=23+1=53 ，
∴C△EGH'=EH'+EG+GH'=EH+EG+GH=103+5+53=5+5
故答案为：5+5.
三、解答题（本题有8小题，第17题6分，第18、19题每题8分，第20、21题10分，第22、23题12分，共66分）
解答应写出文字说明，证明过程或推演步骤.
17．
（1）计算： 12+(2014-π)0-4cs30° ；
（2）先化简，再求值： (x+1-2xx)÷2x-2x ，其中 x=2+1 .
【答案】（1）解：原式=2 3 +1-4× 32 =2 3 +1-2 3 =1；
（2）解：原式= x2+1-2xx×x2(x-1)=(x-1)2x×x2(x-1)=x-12.
当 x=2+1 时,原式= 2+1-12=22.
18．某校在七、八年级举行了“食品安全知识测试”比赛，从七、八年级各随机抽取了10名学生的比赛成绩（百分制），测试成绩整理、描述和分析如下：（成绩得分用 x 表示，共分成四组： A ． 80≤x<85 ， B ． 85≤x<90 ， C ． 90≤x<95 ， D ． 95≤x<100 ）
七年级10名学生的成绩数据是：96，83，96，87，99，96，90，100，89，84．
八年级10名学生成绩数据中，在 C 组中的是：94，90，92．
七，八年级抽取的学生竞赛成绩统计表
八年级抽取的学生成绩扇形统计图
根据以上信息，解答下列问题：
（1）这次比赛中哪个年级成绩更稳定，并说明理由；
（2）求出统计图中 a 的值以及表格中 b 的值；
（3）该校七年级共860人参加了此次比赛，估计参加此次比赛成绩优秀（ x≥90 ）的七年级学生人数是多少？
【答案】（1）解：∵七、八年级的平均数相等，七年级的方差小于八年级的方差，
∴七年级的成绩更稳定；
（2）解：∵八年级A组有10×10%=1人，B组有10×20%=2人，C组有3人，
∵D组人数为10-1-2-3=4，
∴D组的占比为40%，
∴a=40；
∵中位数在C组，
∴第5个数为92，第6个数为94，
∴八年级的中位数b=92+942=93，
∴a=40，b=93；
（3）解：860×610=516，
∴参加此次比赛成绩优秀（x≥90）的七年级学生人数是516人.
19．如图，在△ABC中，边AB绕点B顺时针旋转60°与BC重合，点D、E分别在边BC、AC上，∠ADE＝60°．
（1）求证：△ABD∽△DCE；
（2）若BD＝1，CE＝23，求△ABC的边长．
【答案】（1）证明：在△ABC中，边AB绕点B顺时针旋转60°与BC重合，
∴△ABC为等边三角形，
∴∠ABC＝∠ACB＝60°，AB＝BC，
∴∠BAD+∠BDA＝120°，
∵∠ADE＝60°，
∴∠BDA+∠CDE＝120°，
∴∠BAD＝∠CDE，
∴△ABD∽△DCE；
（2）解：∵△ABD∽△DCE，
∴ABCD=BDCE，
∵BD＝1，CE＝23，
∴ABBC-BD=BDCE，
∴AB＝3，
∴△ABC的边长为3．
20．如图，一次函数y=k1x+b的图像与x轴，y轴分别交于A，B两点，与反比例函数y=k2x的图像分别交于C，D两点，已知点C坐标是(3，6)，AB=BC.
（1）求一次函数y=k1x+b与反比例函数y=k2x的解析式：
（2）直接写出不等式k1x+b（3）求△COD的面积.
【答案】（1）解：如图所示，过点C作CE⊥x轴于E，过点B作BF⊥CE于F，
∵由作图可知，BF∥x轴，
∴∠CBF=∠BAO，∠CFB=∠BOA=90°，且AB=BC，
∴△CBF≌△BAO(AAS)，
∴BO=CF，AO=BF，
∵点C坐标是(3，6)，
∴OE=OA=3，则AE=BE=6，即△ACE为等腰直角三角形，且∠CAE=45°，
∴△BAO，△CBF为等腰直角三角形，
∴A(-3，0)，B(0，3)，
将A(-3，0)，B(0，3)代入一次函数y=k1x+b得，
-3k1+b=0b=3，解方程组得，k1=1b=3，
∴一次函数的解析式为：y=x+3，
把C(3，6)代入反比例函数y=k2x，得k2=18，
∴反比例函数的解析式为：y=18x，
∴一次函数的解析式为：y=x+3，反比例函数的解析式为：y=18x.
（2）解：不等式x+3<18x的解集为：x<-6或0（3）解：如图所示，过点D作DG⊥x轴于G，且A(-3，0)，C(3，6)，D(-6，-3)，
∴OA=3，CF=6，DG=3，
∵S△COD=S△AOD+S△AOC，
∴S△COD=12AO·DG+12AO·CF=12AO·(DG+CF)
∴S△COD=12×3×(3+6)=272，
∴△COD的面积为272.
【解析】（2）由（1）得一次函数的解析式为：y=x+3，反比例函数的解析式为：y=18x，
∴联立方程组求交点得y=x+3y=18x，解方程组得，x=3y=6或x=-6y=-3，
∴D(-6，-3)，
∴不等式x+3<18x的解集为：x<-6或021．如图，点E是正方形ABCD的边AB上的一点，延长BC到F使AE=CF，连接DE、DF.
（1）能通过旋转△DAE得到△DCF吗？说明理由.
（2）连接EF，过D作DM垂直EF于M，交BC于N，若BN=3，CN=2，求AE的长.
【答案】（1）解：能通过旋转△DAE得到△DCF，理由如下：
∵四边形ABCD是正方形，
∴AD=DC，∠A=∠DCB=90°，
∴∠DCE=90°=∠A，
在△DAE和△DCF中，
AD=DC∠A=∠DCFAE=CF，
∴△DAE≌△DCF(SAS)，
∴△DCF可以看作由△DAE绕点D逆时针方向旋转90度得到
（2）解：连接EN，
∵△DAE≌△DCF，
∴AE=CF，DE=DF，
∵DN⊥EF，
∴EM=FFM，
∴DN垂直平分EF，
∴NE=FN，
设AE=CF=x，
∴BE=5-x，EN=FN=3+x，
∵BE2+BN2=EN2，
∴(5-x)2+22=(3+x)2，
解得x=98，
∴AE=98.
22．在平面直角坐标系中，已知二次函数y＝﹣x2+2kx+k﹣1（k是常数）.
（1）当k＝﹣2时，求该二次函数图象与x轴的交点坐标；
（2）若该函数图象经过点（1，4），求该二次函数图象的顶点坐标；
（3）当0≤x≤1时，该函数有最大值4，求k的值.
【答案】（1）解：当k＝﹣2时，二次函数解析式为y＝﹣x2﹣4x﹣3，
令y＝0，则﹣x2﹣4x﹣3＝0，
解得x1＝﹣1，x2＝﹣3，
∴当k＝﹣2时，求该二次函数图象与x轴的交点坐标为（﹣1，0），（﹣3，0）；
（2）解：∵二次函数y＝﹣x2+2kx+k﹣1的图象经过点（1，4），
∴﹣1+2k+k﹣1＝4，
解得k＝2，
∴y＝﹣x2+4x+1＝﹣（x﹣2）2+5，
∴该二次函数图象的顶点坐标为（2，5）；
（3）解：二次函数y＝﹣x2+2kx+k﹣1的对称轴为直线x＝﹣ 2k-2 ＝k，
①k≥1时，
当0≤x≤1时，y随x的增大而增大，
∴当x＝1时，y有最大值，即﹣1+2k+k﹣1＝4，
解得k＝2；
②k≤0时，
当0≤x≤1时，y随x的增大而减小，
∴当x＝0时，y有最大值，即k﹣1＝4，
解得k＝5；
③0＜k＜1时，
当0≤x≤1时，x＝k时，y最大，
∴﹣k2+2k2+k﹣1＝4，
解得k＝ -1±212 （不合题意），
∴k的值为2或5.
23．如图，已知AC为⊙O的直径，连接AB，BC，OB，过点O作OE⊥AB于点E，点F是半径OC的中点，连接EF，BF.
（1）如图1，设⊙O的半径为2，若∠BAC＝30°，求线段EF的长.
（2）如图2，设BO交EF于点P，延长BO交⊙O于点D，连接DF.
①求证：PE＝PF；
②若DF＝EF，求∠BAC的度数.
【答案】（1）解：∵OE⊥AB，∠BAC＝30°，OA＝2，
∴∠AOE＝60°，OE＝12OA＝1，AE＝EB＝3OE＝3，
∵AC是直径，
∴∠ABC＝90°，
∴∠C＝60°，
∵OC＝OB，
∴△OCB是等边三角形，
∵OF＝FC，
∴BF⊥AC，
∴∠AFB＝90°，
∵AE＝EB，
∴EF＝12AB＝3.
（2）解：①证明：如图2中，过点F作FG⊥AB于G，交OB于H，连接EH.
∵∠FGA＝∠ABC＝90°，
∴FG∥BC，
∴△OFH∽△OCB，
∴FHBC=OFOC＝12，同理OEBC＝12，
∴FH＝OE，
∵OE⊥AB.FH⊥AB，
∴OE∥FH，
∴四边形OEHF是平行四边形，
∴PE＝PF.
②解：∵OE∥FG∥BC，
∴EGGB=OFFC＝1，
∴EG＝GB，
∴EF＝FB，
∵DF＝EF，
∴DF＝BF，
∵DO＝OB，
∴FO⊥BD，
∴∠AOB＝90°，
∵OA＝OB，
∴△AOB是等腰直角三角形，
∴∠BAC＝45°.
解法二：可以过E点作EG∥OB交AC于点G，连接DG.
∵EG∥OB，AE＝EB，
∴AG＝OG
∵OF＝FC，
∴OG＝OF，
∴OD﹣FG，
∵AE⊥OE，AG＝OG，
∴EG＝12AO＝OG，
∵∠DOG＝∠FGE，
∴DOG≌△FGE（SAS），
∴DG＝EF，
∵DF＝EF，
∴DG＝DF，
∴DO⊥FG，
∴EG⊥AO，
∴EA＝EO，
∴∠BAC＝45°年级
平均数
中位数
众数
方差
七年级
92
93
96
34.4
八年级
92
b
100
50.4
年级
平均数
中位数
众数
方差
七年级
92
93
96
34.4
八年级
92
b
100
50.4