高中数学高考高考数学一轮复习总教案：3 1　导数的概念与运算

这是一份高中数学高考高考数学一轮复习总教案：3 1　导数的概念与运算，共4页。教案主要包含了变式训练1，变式训练2，变式训练3等内容，欢迎下载使用。

高考导航
知识网络

3.1 导数的概念与运算
典例精析
题型一 导数的概念
【例1】 已知函数f(x)＝2ln 3x＋8x，
求eq \f(f(1－2Δx)－f(1),Δx)的值.
【解析】由导数的定义知：
eq \f(f(1－2Δx)－f(1),Δx)＝－2eq \f(f(1－2Δx)－f(1),－2Δx)＝－2f′(1)＝－20.
【点拨】导数的实质是求函数值相对于自变量的变化率，即求当Δx→0时， 平均变化率eq \f(Δy,Δx)的极限.
【变式训练1】某市在一次降雨过程中，降雨量y(mm)与时间t(min)的函数关系可以近似地表示为f(t)＝eq \f(t2,100)，则在时刻t＝10 min的降雨强度为( )
A.eq \f(1,5) mm/minB.eq \f(1,4) mm/min
C.eq \f(1,2) mm/minD.1 mm/min
【解析】选A.
题型二 求导函数
【例2】 求下列函数的导数.
(1)y＝ln(x＋eq \r(1＋x2))；
(2)y＝(x2－2x＋3)e2x；
(3)y＝eq \r(3,\f(x,1－x)).
【解析】运用求导数公式及复合函数求导数法则.
(1)y′＝eq \f(1,x＋\r(1＋x2))(x＋eq \r(1＋x2))′
＝eq \f(1,x＋\r(1＋x2))(1＋eq \f(x,\r(1＋x2)))＝eq \f(1,\r(1＋x2)).
(2)y′＝(2x－2)e2x＋2(x2－2x＋3)e2x
＝2(x2－x＋2)e2x.
(3)y′＝eq \f(1,3)(eq \f(x,1－x)eq \f(1－x＋x,(1－x)2)
＝eq \f(1,3)(eq \f(x,1－x)eq \f(1,(1－x)2)
＝eq \f(1,3)x (1－x)
【变式训练2】如下图，函数f(x)的图象是折线段ABC，其中A、B、C的坐标分别为(0,4)，(2,0)，(6,4)，则f(f(0))＝ ；eq \f(f(1＋Δx)－f(1),Δx)＝ (用数字作答).
【解析】f(0)＝4，f(f(0))＝f(4)＝2，
由导数定义eq \f(f(1＋Δx)－f(1),Δx)＝f′(1).
当0≤x≤2时，f(x)＝4－2x，f′(x)＝－2，f′(1)＝－2.
题型三 利用导数求切线的斜率
【例3】 已知曲线C：y＝x3－3x2＋2x， 直线l：y＝kx，且l与C切于点P(x0，y0) (x0≠0)，求直线l的方程及切点坐标.
【解析】由l过原点，知k＝eq \f(y0,x0) (x0≠0)，又点P(x0，y0) 在曲线C上，y0＝xeq \\al(3,0)－3xeq \\al(2,0)＋2x0，
所以 eq \f(y0,x0)＝xeq \\al(2,0)－3x0＋2.
而y′＝3x2－6x＋2，k＝3xeq \\al(2,0)－6x0＋2.
又 k＝eq \f(y0,x0)，
所以3xeq \\al(2,0)－6x0＋2＝xeq \\al(2,0)－3x0＋2，其中x0≠0，
解得x0＝eq \f(3,2).
所以y0＝－eq \f(3,8)，所以k＝eq \f(y0,x0)＝－eq \f(1,4)，
所以直线l的方程为y＝－eq \f(1,4)x，切点坐标为(eq \f(3,2)，－eq \f(3,8)).
【点拨】利用切点在曲线上，又曲线在切点处的切线的斜率为曲线在该点处的导数来列方程，即可求得切点的坐标.
【变式训练3】若函数y＝x3－3x＋4的切线经过点(－2，2)，求此切线方程.
【解析】设切点为P(x0，y0)，则由
y′＝3x2－3得切线的斜率为k＝3xeq \\al(2,0)－3.
所以函数y＝x3－3x＋4在P(x0，y0)处的切线方程为
y－y0＝(3xeq \\al(2,0)－3)(x－x0).
又切线经过点(－2,2)，得
2－y0＝(3xeq \\al(2,0)－3)(－2－x0)，①
而切点在曲线上，得y0＝xeq \\al(3,0)－3x0＋4， ②
由①②解得x0＝1或x0＝－2.
则切线方程为y＝2 或 9x－y＋20＝0.
总结提高
1.函数y＝f(x)在x＝x0处的导数通常有以下两种求法：
(1) 导数的定义，即求eq \f(Δy,Δx)＝eq \f(f(x0＋Δx)－f(x0),Δx)的值；
(2)先求导函数f′(x)，再将x＝x0的值代入，即得f′(x0)的值.
2.求y＝f(x)的导函数的几种方法：
(1)利用常见函数的导数公式；
(2)利用四则运算的导数公式；
(3)利用复合函数的求导方法.
3.导数的几何意义：函数y＝f(x)在x＝x0处的导数f′(x0)，就是函数y＝f(x)的曲线在点P(x0，y0)处的切线的斜率.
天星教育网 来源：天星教育
Tesn

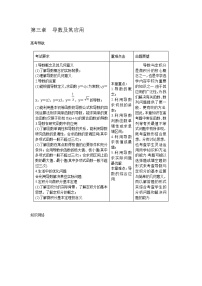
来源：天~星~教~育~网考试要求
重难点击
命题展望
1.导数概念及其几何意义
(1)了解导数概念的实际背景；
(2)理解导数的几何意义.
2.导数的运算
(1)能根据导数定义，求函数y＝c(c为常数)，y＝x，y＝x2，y＝x3，y＝，y＝的导数；
(2)能利用基本初等函数的导数公式和导数的四则运算法则求简单函数的导数，能求简单的复合函数(仅限于形如f(ax＋b)的复合函数)的导数.
3.导数在研究函数中的应用
(1)了解函数单调性和导数的关系，能利用导数研究函数的单调性，会求函数的单调区间(其中多项式函数一般不超过三次)；
(2)了解函数在某点取得极值的必要条件和充分条件；会用导数求函数的极大值、极小值(其中多项式函数一般不超过三次)；会求闭区间上函数的最大值、最小值(其中多项式函数一般不超过三次).
4.生活中的优化问题
会利用导数解决某些实际问题.
5.定积分与微积分基本定理
(1)了解定积分的实际背景，了解定积分的基本思想，了解定积分的概念；
(2)了解微积分基本定理的含义.
本章重点：
1.导数的概念；
2.利用导数求切线的斜率；
3.利用导数判断函数单调性或求单调区间；
4.利用导数求极值或最值；
5.利用导数求实际问题最优解.
本章难点：导数的综合应用.
导数与定积分是微积分的核心概念之一，也是中学选学内容中较为重要的知识之一.由于其应用的广泛性，为我们解决有关函数、数列问题提供了更一般、更有效的方法.因此，本章知识在高考题中常在函数、数列等有关最值不等式问题中有所体现，既考查数形结合思想，分类讨论思想，也考查学生灵活运用所学知识和方法的能力.考题可能以选择题或填空题的形式来考查导数与定积分的基本运算与简单的几何意义，而以解答题的形式来综合考查学生的分析问题和解决问题的能力.