贵州省六盘水市钟山区2022-2023学年九年级上学期期末数学试题（含答案）

这是一份贵州省六盘水市钟山区2022-2023学年九年级上学期期末数学试题（含答案），共23页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
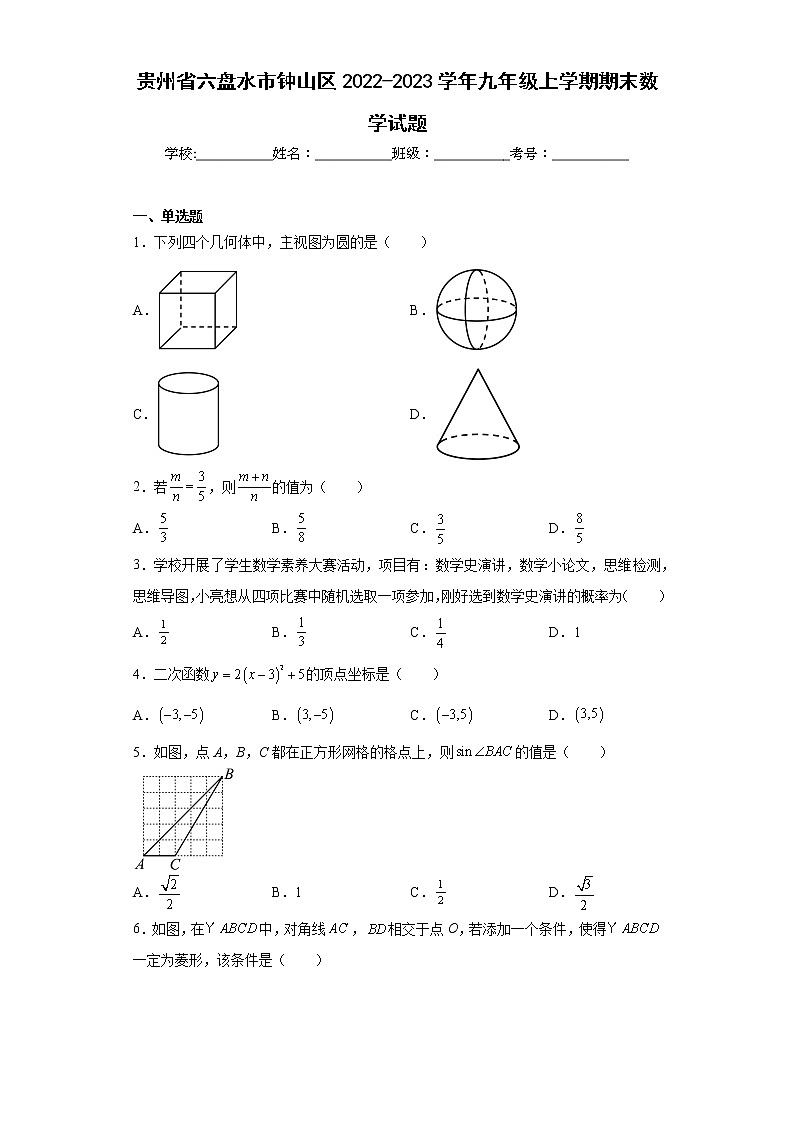
1．下列四个几何体中，主视图为圆的是（ ）
A．B．
C．D．
2．若，则的值为（ ）
A．B．C．D．
3．学校开展了学生数学素养大赛活动，项目有：数学史演讲，数学小论文，思维检测，思维导图，小亮想从四项比赛中随机选取一项参加，刚好选到数学史演讲的概率为（ ）
A．B．C．D．
4．二次函数的顶点坐标是（ ）
A．B．C．D．
5．如图，点A，B，C都在正方形网格的格点上，则的值是（ ）
A．B．1C．D．
6．如图，在中，对角线，相交于点O，若添加一个条件，使得一定为菱形，该条件是（ ）
A．B．C．D．
7．反比例函数的图象上有两点，．则m与n的大小关系为（ ）
A．B．C．D．
8．如图，在平面直角坐标系中，与是位似图形，且顶点都在格点上，则位似中心的坐标是（ ）
A．B．C．D．
9．如图，在中，点D，E分别在，上，且，四边形的面积是面积的3倍．若，则的长为（ ）
A．10B．15C．20D．24
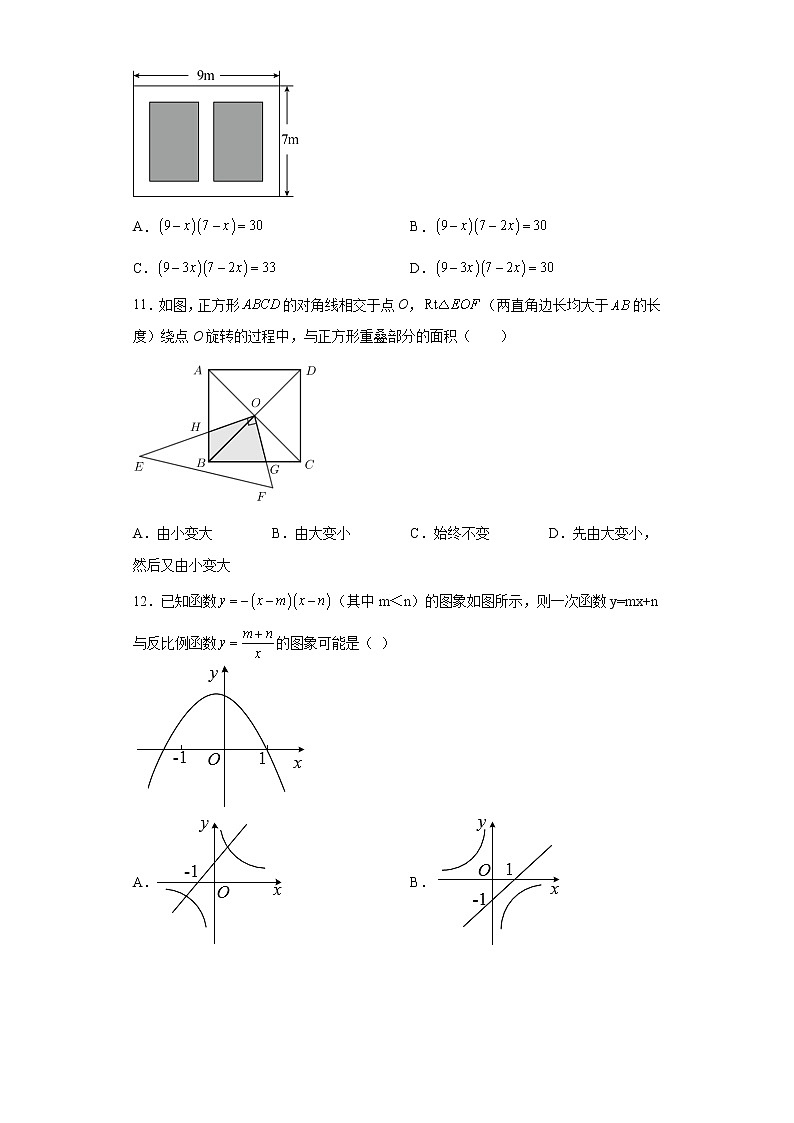
10．九（1）班分到如图所示一块长为9m，宽为7m的矩形空地，计划在其中两块完全相同的矩形地种植蔬菜，它们的面积之和为，若人行道的宽度都为x，则可以列出关于x的方程（ ）
A．B．
C．D．
11．如图，正方形的对角线相交于点O，（两直角边长均大于的长度）绕点O旋转的过程中，与正方形重叠部分的面积（ ）
A．由小变大B．由大变小C．始终不变D．先由大变小，然后又由小变大
12．已知函数（其中m＜n）的图象如图所示，则一次函数y=mx+n与反比例函数的图象可能是（ ）
A．B．C．D．
二、填空题
13．一元二次方程x（x﹣3）=0的解是________．
14．学校的生物兴趣小组在老师的指导下，对某种植物种子发芽率进行研究时所得到的数据如下表：
依据上表的数据，估计这种植物种子在该实验条件下发芽的概率是___________．（结果精确到）
15．如图，在菱形中，对角线，的长分别为6，8，过点A作于点E，则的长为___________．
16．如图，在平面直角坐标系中，点在y轴正半轴上，点在x轴正半轴上，点N为线段上一动点，点M为线段上一动点，当的值最小时N点的坐标为___________．
三、解答题
17．如图，在中，为对角线．
(1)用尺规作出的垂直平分线，分别交，于点E，F，不写作法，保留作图痕迹；
(2)若的周长为10，求的周长．
18．为了解学生参加学校社团活动的情况，对报名参加A：篮球，B：舞蹈，C：书法，D：田径，E：绘画这五项活动的学生（每人必选且只能参加一项）中随机抽取了部分学生进行调查，并将调查结果绘制成如下两幅不完整的统计图．
根据所给的信息，解答下列问题：
(1)这次被调查的学生共有___________人，并把条形统计图补充完整；
(2)若该校共有名学生参加社团活动，请你估计这名学生中约有多少人参加书法社团；
(3)在田径社团活动中，由于甲，乙，丙，丁四人平均的成绩突出，现决定从他们中任选两名参加区级运动会．用树状图或列表的方法求恰好选中甲，乙两位同学参加的概率．
19．关于x的一元二次方程：有实数根．
(1)求m的取值范围；
(2)若，是方程的两根，且，求m的值．
20．如图，在矩形中，对角线、相交于点O，交的延长线于点E．
(1)判断四边形的形状，并说明理由；
(2)若，，求四边形的面积．
21．星辉超市销售规格为500克每包的金丝菊，每包的进价为100元，调查发现，当销售价为108元每包时，每月可售出180包，而当销售价每降价1元，平均每月可多售20包，超市要想使该规格的金丝黄菊的销售利润平均每月达到1320元，则每包金丝黄菊的定价应为多少元？
22．如图，学校从教学楼顶悬挂了一幅长为的励志条幅，已知楼顶到地面的距离为18m，在楼前点A处，测得条幅底端N的仰角为，在距A点12m处的B点（点A，B，C在一条直线上），测得条幅顶端M的仰角为，若忽略测量仪器的高度，请你计算：（结果保留根号）
(1)求的长；
(2)求条幅的长度．
23．如图，一次函数（k为常数，）的图像与x轴，y轴分别交于，两点，且，与反比例函数（m为常数，且）的图像交于C，E两点，过点C作轴于点D，且．
(1)求一次函数与反比例函数的解析式；
(2)求的面积；
(3)直接写出不等式的解集．
24．如图，在中，，点P，D分别在，边上，连接，，且．
(1)求证：；
(2)，，当点P为中点时，求的长．
25．如图1，抛物线与x轴交于，两点，与y轴交于点C．
(1)填空：___________，___________；
(2)求直线的解析式；
(3)将抛物线位于x轴下方的图像沿x轴翻折到x轴上方，得到如图2所示的新图像，平移直线得到函数，当直线与新图像有三个公共点时，求n的值．
每批粒数
发芽的频数
发芽的频率
参考答案：
1．B
【分析】根据几何体的主视图是否为圆进行判断即可．
【详解】解：A、长方体的主视图是长方形，不合题意；
B、球的主视图是圆，符合题意；
C、圆柱的主视图是长方形，不合题意；
D、圆锥的主视图是三角形，不合题意；
故选：B．
【点睛】本题主要考查了三视图，解题关键要注意：从正面看到的图形是主视图．
2．D
【分析】把化成，再把代入即可得出答案．
【详解】解：，
．
故选D．
【点睛】此题考查比例的性质，解题的关键是把化成，属于较简单运算．
3．C
【分析】共有四项比赛，抽中每项的概率是相等的，因此根据简单概率公式计算即可．
【详解】解：从四项比赛（数学史演讲，数学小论文，思维检测，思维导图）中随机选取一项参加，刚好选到数学史演讲的概率为，
故选C．
【点睛】本题考查简单概率计算，理解概率的意义是解题的关键．
4．D
【分析】根据顶点式可直接写出顶点坐标．
【详解】解：∵抛物线解析式为，当时，y取最大值，最大值是5，
∴二次函数图象的顶点坐标是．
故选D．
【点睛】本题主要考查二次函数的顶点，解题的关键是熟知顶点式的特点．
5．A
【分析】勾股定理求出的长，利用正弦的定义，进行计算即可．
【详解】解：设小正方形的边长为1，由勾股定理，得：，
过点作，
由图可知：，
∴；
故选A．
【点睛】本题考查网格中计算三角函数值．熟练掌握锐角三角函数的定义，是解题的关键．
6．C
【分析】根据平行四边形的性质、菱形的判定方法一一判断即可．
【详解】解：A. ，可以判断平行四边形是矩形，不能判断是菱形，故该选项错误；
B. ，可以判断平行四边形是矩形，不能判断是菱形，故该选项错误；
C. ，可以判断平行四边形是菱形；
D. ，只能推出，无法判定是菱形．
故选C．
【点睛】此题主要考查了菱形的判定，解题的关键是掌握菱形的判定方法：①菱形定义：一组邻边相等的平行四边形是菱形；②四条边都相等的四边形是菱形；③对角线互相垂直的平行四边形是菱形（或“对角线互相垂直平分的四边形是菱形”）．
7．A
【分析】根据反比例函数的性质，进行判断即可．
【详解】解：∵，，
∴双曲线过一、三象限，在每一个象限内，随的增大而减小，
∵，
∴；
故选A．
【点睛】本题考查比较反比例函数的函数值大小．熟练掌握反比例函数的性质，是解题的关键．
8．B
【分析】根据位似图形的定义，画出位似中心，即可得出结果．
【详解】解：∵与是位似图形，
连接并延长，交于点，则点即为位似中心，如图所示：
由图可知：；
故选B．
【点睛】本题考查坐标系下求位似中心的坐标．熟练掌握位似图形的定义，确定位似中心的位置，是解题的关键．
9．A
【分析】证明，利用面积比等于相似比的平方，求出相似比，进而求出的长即可．
【详解】解：∵四边形的面积是面积的3倍，
∴的面积是面积的4倍，
∵，，
∴，
∵的面积是面积的4倍，
∴，
∴；
故选A．
【点睛】本题考查相似三角形的判定和性质．熟练掌握相似三角形的判定方法，证明三角形相似，是解题的关键．
10．D
【分析】人行道的宽度都为x，根据两块完全相同的矩形的面积之和为，列出方程即可．
【详解】解：人行道的宽度都为x，由题意，得：；
故选D．
【点睛】本题考查一元二次方程的应用．正确的识图，确定矩形的长和宽，列出方程，是解题的关键．
11．C
【分析】由条件可得，从而，，即可说明重叠面积始终不变．
【详解】解：正方形中，，，，，
，
，
在与中，，
，
，
，
则重叠部分的面积始终不变，
故选：C．
【点睛】本题考查了三角形全等的判定与性质，利用面积的等量代换是解题关键．
12．C
【分析】根据二次函数图象判断出m＜﹣1，n=1，然后求出m+n＜0，再根据一次函数与反比例函数图象的性质判断即可．
【详解】解：由图可知，m＜﹣1，n=1，
∴m+n＜0，
∴一次函数y=mx+n经过第一、二、四象限，且与y轴相交于点（0，1），
反比例函数的图象位于第二、四象限；
故选C．
【点睛】本题考查了二次函数图象，一次函数图象，反比例函数图象，观察二次函数图象判断出m、n的取值是解题的关键．
13．，；
【分析】根据两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.
【详解】x(x-3)=0，
x=0，x-3=0，
x1=0，x2=3.
【点睛】此题考查了解一元二次方程,熟练掌握因式分解法是解题发关键.
14．
【分析】概率是大量重复试验的情况下，频率的稳定值可以作为概率的估计值，即次数越多的频率越接近于概率．
【详解】解：由数据可知，每批颗粒数越多时发芽的频率越稳定在，
则估计这种植物种子在该实验条件下发芽的概率是，
故答案为：．
【点睛】本题考查了利用频率估计概率，大量重复试验下频率稳定值即概率，掌握相关知识的解题关键．
15．
【分析】利用菱形的性质和勾股定理求出菱形的边长，利用等积法求出的长即可．
【详解】解：∵在菱形中，对角线，的长分别为6，8，
∴，
∴，
∵，
∴菱形的面积，即：，
∴；
故答案为：．
【点睛】本题考查菱形性质．熟练掌握菱形的对角线互相垂直平分，是解题的关键．
16．##
【分析】作点B关于y轴的对称点，作于点，交y轴于点，则，，进而可得，因此即为的最小值，证明，利用对应边成比例求出的长度即可得出N点的坐标．
【详解】解：如图所示，作点B关于y轴的对称点，作于点，交y轴于点，连接，．
由轴对称的性质可得，
则，
，，
，，
，
，
，
，
又，
，
，即，
，
当的值最小时N点的坐标为．
故答案为：．
【点睛】本题考查利用轴对称求线段的最值，相似三角形的判定与性质，解题的关键是找出取最小值时N点的位置．
17．(1)见解析
(2)20
【分析】（1）分别以A，C为圆心，大于长为半径作弧，在线段两侧分别得到一个交点，连接两个交点即可；
（2）连接．根据线段的垂直平分线的性质可得，进而根据的周长为10，可得，再根据平行四边形对边相等即可求出的周长．
【详解】（1）解：如图所示，直线即为的垂直平分线；
（2）解：如图，连接．
点E在线段的垂直平分线上，
，
的周长为10，
，
，
的周长．
【点睛】本题考查尺规作图——线段的垂直平分线的作法，线段的垂直平分线的性质，平行四边形的性质，解题的关键是掌握线段的垂直平分线上的点到线段两端的距离相等．
18．(1)，图见解析
(2)
(3)，图见解析
【分析】（1）用篮球人数除以所占百分比即可求出调查的学生总人数，用总人数减去除田径外其他项目的人数即可得到参加田径的人数，然后补充条形统计图即可；
（2）先计算出参加书法社团的百分比，然后用相乘即可；
（3）画出树状图，然后根据树状图计算概率即可．
【详解】（1）解：被调查的学生共有（人），
参加田径的人数为（人），
条形统计图补充完整如下图所示，
（2）解：（人），
答：这名学生中约有人参加书法社团．
（3）解：如图所示，
由图可知，甲乙两位同学参加有种情况，总共有种情况，
则恰好选中甲，乙两位同学参加的概率为．
【点睛】本题考查了条形统计图与扇形统计图综合，树状图与概率计算，掌握相关知识并正确计算是解题关键．
19．(1)
(2)2
【分析】（1）根据有实数根，可得，然后解不等式即可；
（2）根据根与系数的关系得到求出，，代入已知等式中，求出m值即可．
【详解】（1）解：∵方程有实数根，
∴，
∴；
（2）解：∵，是方程的两个根，
∴，，
∵，
∴，
解得：，
即m的值是2．
【点睛】本题考查了一元二次方程的根的判别式，一元二次方程根与系数的关系，解题的关键是掌握：当，方程有两个不相等的实数根；当，方程有两个相等的实数根；当，方程没有实数根．
20．(1)四边形为平行四边形；理由见解析
(2)
【分析】（1）根据矩形得出，再根据即可得出四边形为平行四边形；
（2）根据矩形的性质，结合直角三角形的性质，求出，，根据平行四边形的性质，求出，最后根据梯形面积公式求出结果即可．
【详解】（1）解：四边形为平行四边形；理由如下：
∵四边形为矩形，
∴，
∵，
∴四边形为平行四边形；
（2）解：∵四边形为矩形，
∴，，，，
∵，
∴，
∵，
∴，
∴，，
∵四边形为平行四边形，
∴，
∴，
∴．
【点睛】本题主要考查了矩形的性质，平行四边形的判定和性质，勾股定理，直角三角形的性质，解题的关键是熟练掌握矩形的性质和平行四边形的判定方法．
21．每包金丝黄菊的定价应为元
【分析】设每包金丝黄菊的定价为元，根据题意，列出一元二次方程，进行求解即可．
【详解】解：设每包金丝黄菊的定价为元，由题意，得：，
整理，得：，
解得：（不合题意，舍去）；
答：每包金丝黄菊的定价应为元．
【点睛】本题考查一元二次方程应用．找准等量关系，准确的列出一元二次方程，是解题的关键．
22．(1)
(2)的长度为
【分析】（1）在中，利用，求出的长，利用求出的长即可；
（2）在中，利用，求出的长，利用求出的长即可．
【详解】（1）解：由题意，得：，，，
在中，，
∴，
∴；
（2）解：在中，，
∴，
∴．
答：的长度为．
【点睛】本题考查解直角三角形．熟练掌握锐角三角函数的定义，熟记特殊角的三角函数值，是解题的关键．
23．(1)，
(2)
(3)或
【分析】（1）用含代数式表示出，两点的坐标，然后根据即可求出，然后再将点C的横坐标代入求出纵坐标，最后将点C的坐标代入即可求出；
（2）将一次函数与反比例函数联立即可求出点的坐标，然后即可计算的面积；
（3）根据点和点的横坐标，结合图像，找到反比例函数图像在一次函数图像下方时对应的范围即可．
【详解】（1）解：当代入得；当代入得，
故，，
，
，
一次函数解析式为：，
，
点C的横坐标为，将代入得，
即点C的坐标为，将点C的坐标代入得，
，
反比例函数的解析式为：；
故一次函数解析式为：，反比例函数的解析式为：．
（2）解：将一次函数与反比例函数联立得，
解得或，
故点的坐标为，点到轴的距离为，
；
（3）解：由（2）可知点的坐标为，点的坐标为，
，
根据图像可得：或．
【点睛】本题考查了一次函数与反比例函数结合的图像性质，利用图像解不等式等知识，采用待定系数法求函数解析式是解题关键．
24．(1)见解析
(2)
【分析】（1）由题意可得，，可证；
（2）由，可得，代入数值即可求出的长．
【详解】（1）证明：，
，
，
，
又，
，
；
（2）解：，点P为中点，
，
，
，即，
解得．
【点睛】本题考查了相似三角形的判定与性质，等腰三角形的性质，熟练掌握相似三角形的性质是解题的关键．
25．(1)；3
(2)
(3)或
【分析】（1）将，两点，代入，即可求出b、c的值；
（2）用待定系数法求值的解析式即可；
（3）分两种情况，当直线过点B或直线与抛物线相切时，分别求出n的值即可．
【详解】（1）解：将，两点，代入得：
，
解得：，
故答案为：；3．
（2）解：抛物线解析式为，
把代入得：，
∴点C的坐标为，
设直线的解析式为，
把，代入得：
，
解得：，
∴直线的解析式为．
（3）解：∵直线由直线平移得到，
∴，
抛物线在x轴下方图像沿x轴翻折得到的新图像解析式为：
，
如图，当直线过点B或直线与抛物线相切时，直线与新图像有三个公共点，
当直线过点B时，把代入得：
，
解得：；
当直线与与抛物线相切时，
联立，
，
整理得：，
，
解得：；
综上分析可知，或．
【点睛】本题主要考查了二次函数的综合应用，求二次函数解析式，求一次函数的解析式，一次函数与二次函数的交点问题，解题的关键是熟练直线的平移特点，数形结合，注意分类讨论．