2023届江西省景德镇市第一中学重点中学盟校高三下学期第一次联考（月考）数学文试卷含答案

江西省重点中学盟校2023届高三第一次联考数学（文）试题

一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 设集合， 则选项正确的是（    ）

A.  B.

C.  D.

2. 已知，均为实数，复数，，，则（  ）

A.  B.  C.  D.

3. 已知，则是的（    ）

A. 充要条件 B. 充分不必要条件

C. 必要不充分条件 D. 既不充分也不必要条件

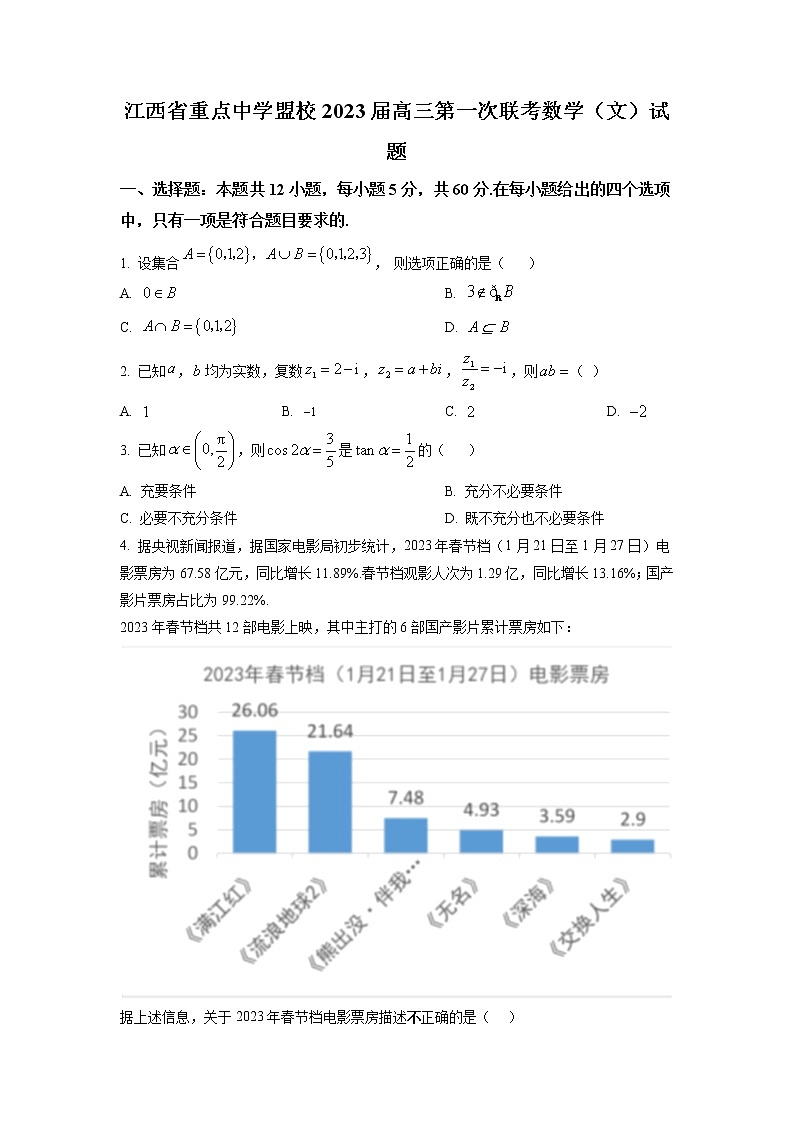
4. 据央视新闻报道，据国家电影局初步统计，2023年春节档（1月21日至1月27日）电影票房为67.58亿元，同比增长11.89%.春节档观影人次为1.29亿，同比增长13.16%；国产影片票房占比为99.22%.

2023年春节档共12部电影上映，其中主打的6部国产影片累计票房如下：

据上述信息，关于2023年春节档电影票房描述不正确的是（   ）

A. 主打的6部国产影片总票房约占2023春节档电影票房的.

B. 2023年春节档非国产电影票房约0.98亿元.

C. 主打的6部国产影片票房的中位数为6.205亿元.

D. 电影《交换人生》的票房约为主打的6部国产影片外的其他春节档电影票房总的3倍.

5. 已知向量，，则向量在上投影等于（  ）

A.  B.  C.  D. 7

6. 设函数定义域为，则函数与函数的图象关于（　  ）

A. 直线对称 B. 直线对称

C 直线对称 D. 直线对称

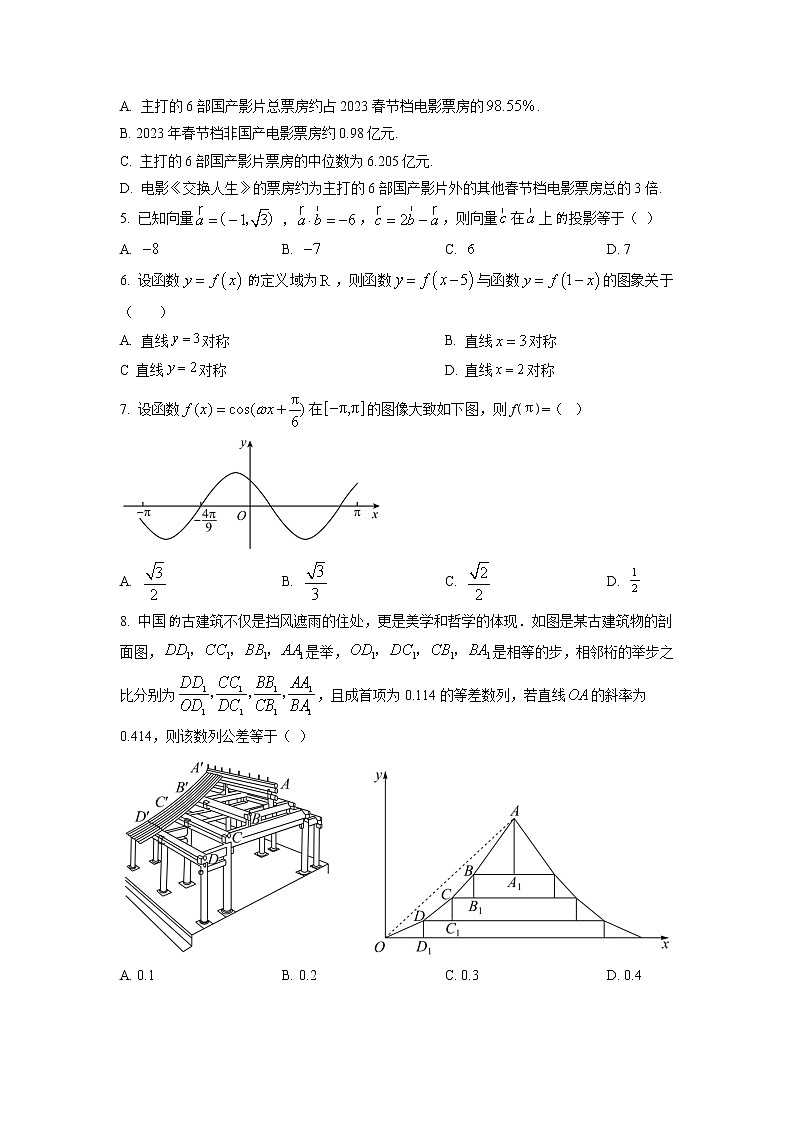
7. 设函数在的图像大致如下图，则f()=（  ）

A.  B.  C.  D.

8. 中国古建筑不仅是挡风遮雨的住处，更是美学和哲学的体现．如图是某古建筑物的剖面图，是举，是相等的步，相邻桁的举步之比分别为，且成首项为0.114的等差数列，若直线的斜率为0.414，则该数列公差等于（  ）

A. 0.1 B. 0.2 C. 0.3 D. 0.4

9. 已知函数为奇函数，则在处的切线方程为（　　）

A.  B.

C.  D.

10. 已知球是正三棱锥的外接球，D是的中点，且，侧棱，则球O的表面积为（    ）

A. 12 B. 8 C. 32 D. 48

11. 已知抛物线的焦点F与双曲线=1的右焦点重合，该抛物线的准线与x轴的交点为K，点A在抛物线上且，则A点的横坐标为（    ）

A.  B. 2 C.  D. 5

12. 已知函数，其导函数的两根为，，若不等式的解集为，且，则极大值为（   ）

A.  B.  C.  D.

二、填空题：本题共4小题，每小题5分，共20分.

13. 若实数，满足约束条件则的最小值为 _______.

14. 已知椭圆的中心在原点，焦点在y轴上，离心率为，请写出一个符合上述条件的椭圆的标准方程__________.

15. 记数列的前项和为，则________.

16. 在正四棱柱中，，E 为中点，为正四棱柱表面上一点，且，则点的轨迹的长为_____.

三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.

（一）必考题：60分.

17. 为了提高学习数学的兴趣，形成良好的数学学习氛围，某校将举行“‘象山杯’数学解题能力比赛”，每班派人参加，某班级老师已经确定参赛名额，第个参赛名额在甲，乙同学间产生，为了比较甲，乙两人解答某种题型的能力，现随机抽取这两个同学各次之前该题型的解答结果如下：，，，，，，，，，，其中，分别表示甲正确和错误；，分别表示乙正确和错误．

（1）若解答正确给该同学分，否则记分．试计算甲、乙两人之前的成绩的平均数和方差，并根据结果推荐谁参加比赛更合适；

（2）若再安排甲、乙两人解答一次该题型试题，试估计恰有一人解答正确的概率.

18. 在中，内角A，B，C的对边分别为a，b，c，且满足．

（1）求角A；

（2）若的面积为，D为BC边上一点，且BD=2CD，求AD的最小值．

19. 如图：在四棱锥中，底面为平行四边形，为线段上一点，且，平面与侧棱交于点.

（1）求；

（2）平面将四棱锥分成了上下两部分，求四棱锥和多面体的体积之比.

20. 设函数．

（1）当时，求函数在定义域内的最小值；

（2）若求实数的取值范围．

21. 已知圆过点，，.

（1）求圆的标准方程；

（2）若过点且与轴平行直线与圆交于点，，点为直线上的动点，直线，与圆的另一个交点分别为，（与不重合），证明：直线过定点.

（二）选考题：共10分.请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分.

[选修4－4：坐标系与参数方程]

22. 在直角坐标系中，曲线的参数方程为（为参数）以坐标原点为极点，以轴正半轴为极轴建立极坐标系，曲线的极坐标方程为

（1）求曲线和曲线的直角坐标方程;

（2）若曲线和曲线交于、两点，且点，求的值.

[选修4－5：不等式选讲]

23. 已知函数

（1）若，解不等式;

（2）若，且的最小值为求证.

江西省重点中学盟校2023届高三第一次联考数学（文）试题

一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1.【答案】B

2.【答案】C

3.【答案】A

4.【答案】B

5.【答案】A

6.【答案】B

7.【答案】D

8.【答案】B

9.【答案】C

10.【答案】D

11.【答案】D

12.【答案】D

二、填空题：本题共4小题，每小题5分，共20分.

13.

【答案】##3.5

14.

【答案】

15. 【答案】##

16.

【答案】##

三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.

（一）必考题：60分.

17. 为了提高学习数学的兴趣，形成良好的数学学习氛围，某校将举行“‘象山杯’数学解题能力比赛”，每班派人参加，某班级老师已经确定参赛名额，第个参赛名额在甲，乙同学间产生，为了比较甲，乙两人解答某种题型的能力，现随机抽取这两个同学各次之前该题型的解答结果如下：，，，，，，，，，，其中，分别表示甲正确和错误；，分别表示乙正确和错误．

（1）若解答正确给该同学分，否则记分．试计算甲、乙两人之前的成绩的平均数和方差，并根据结果推荐谁参加比赛更合适；

（2）若再安排甲、乙两人解答一次该题型试题，试估计恰有一人解答正确的概率.

【答案】（1）甲的平均数为，方差为，乙的平均数为，方差为，推荐乙参加比赛更合适   

（2）

【解析】

【分析】（1）根据平均数与方差的公式分别计算甲、乙两人的平均数与方程，进而推荐人选；

（2）利用古典概型的概率公式估计恰有一人正确的概率.

【小问1详解】

由已知得甲的平均数，方差；

乙的平均数，方差，

因为，且，

所以推荐乙参加比赛更合适；

【小问2详解】

由已知的个结果中，恰有一人解答正确的结果是，，，共个，

所以恰有一人正确的概率为.

18. 在中，内角A，B，C的对边分别为a，b，c，且满足．

（1）求角A；

（2）若的面积为，D为BC边上一点，且BD=2CD，求AD的最小值．

【答案】（1）；   

（2）.

【解析】

【分析】（1）根据正弦定理，结合三角恒等变换可得到，从而可得出答案；

（2）由已知结合三角形的面积公式可求得，根据向量的线性表示及向量的数量积的性质和基本不等式即可求解．

【小问1详解】

由正弦定理得，

又，则，

化简得，

又，则，

所以，所以；

【小问2详解】

由（1）得，则，得，

又BD=2CD，则，

所以，

当且仅当，即，时等号成立，

所以最小值为．

19. 如图：在四棱锥中，底面为平行四边形，为线段上一点，且，平面与侧棱交于点.

（1）求；

（2）平面将四棱锥分成了上下两部分，求四棱锥和多面体的体积之比.

【答案】（1）；   

（2）.

【解析】

【分析】（1）根据线面平行的判定定理和性质定理，结合平行线的性质进行求解即可；

（2）根据棱锥的体积公式，结合棱锥的性质进行求解即可.

【小问1详解】

因为为平行四边形，所以，

因为平面，平面，

所以平面，因为平面与侧棱交于点，

所以平面平面，而平面，

于是有，

所以；

【小问2详解】

设四棱锥的体积为，

由（1）可知： ，所以到平面的距离与到平面的距离满足：，因此，

因为，所以，即，

，

因为，所以，

由，

所以，

所以.

20. 设函数．

（1）当时，求函数在定义域内的最小值；

（2）若求实数的取值范围．

【答案】（1）1    （2）

【解析】

【分析】(1)对求导判断其单调性，从而可求得最小值；

(2)令，则问题转化为当恒成立求实数的取值范围.对求导，分类讨论判断可知当时有最小值从而可求；当时没办法确定最小值，可通过确定来判断不成立.

【小问1详解】

当时，，其定义域为，

则.

令.

当时，；当时，

所以在上单调递减，在上单调递增.

故函数在定义域内的最小值为.

【小问2详解】

令，

即恒成立.

①当时，令.

当时，，单调递减；当时，单调递增.

所以，原不等式成立.

②当时，时，单调递增.

所以当时，，所以不成立.

③当时，时，单调递减.

所以当时，，所以不成立.

④当时，令又，

，

所以不成立.

综上所述，实数的取值范围为.

【点睛】关键点点睛：

第二问可以转化为恒成立.从而确定的最小值.当时没办法确定最小值，可通过确定来判断不成立.

21. 已知圆过点，，.

（1）求圆的标准方程；

（2）若过点且与轴平行的直线与圆交于点，，点为直线上的动点，直线，与圆的另一个交点分别为，（与不重合），证明：直线过定点.

【答案】（1）   

（2）

【解析】

【分析】（1）利用待定系数法求得圆一般方程，再将其转化为标准方程；

（2）求出点，的坐标，设，根据，得出，的坐标，当直线斜率存在时，设直线方程为，与圆方差联立方程组，利用根与系数关系化简得出与的关系，进而得出直线恒过的定点坐标，再验证斜率不存在时仍成立.

【小问1详解】

设圆一般方程为，

又圆过点，，，

则，

解得，

所以圆的一般方程为，

即其标准方程为；

【小问2详解】

由题意得，所以直线，点，点，

设点，，，

所以，，

所以，

又，，

，

又，在圆上，

所以，，

，

即，

所以，

整理得：，

当直线斜率存在时，设直线的方程为，

代入，

得，

则，，

所以，

即，

即，

得或，

当时，直线的方程为，过点，

当时，直线的方程为，过点，在直线上，不成立，

当直线斜率不存在时，，即，解得或（舍），所以直线过成立，

综上所述，直线恒过点.

（二）选考题：共10分.请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分.

[选修4－4：坐标系与参数方程]

22. 在直角坐标系中，曲线的参数方程为（为参数）以坐标原点为极点，以轴正半轴为极轴建立极坐标系，曲线的极坐标方程为

（1）求曲线和曲线的直角坐标方程;

（2）若曲线和曲线交于、两点，且点，求的值.

【答案】（1），   

（2）

【解析】

【分析】（1）利用消参法可得的直角坐标方程，再利用极坐标与直角坐标的转化公式可得的直角坐标方程；

（2）利用直线参数方程的几何意义直接计算.

【小问1详解】

由的参数方程为（为参数），

消参可得，即；

又的极坐标方程为，即，，

所以，

即

【小问2详解】

由（1）的，即

将的参数方程转化为标准参数方程（为参数）

代入得，即，

，，

又由的参数方程可知过点，

所以.

[选修4－5：不等式选讲]

23. 已知函数

（1）若，解不等式;

（2）若，且的最小值为求证.

【答案】（1）   

（2）证明见解析

【解析】

【分析】（1）对绝对值函数进行分段讨论，解不等式即可；

（2）利用三角不等式求得的最小值，得到，再利用基本不等式证明即可．

【小问1详解】

当时，函数

①当时，由，即，解得，所以，

②当时，由，即，解得，所以；

③当时，由，即，解得，所以.

综上，不等式的解集为.

【小问2详解】

因为，

当，即时，取到最小值，

所以，即.

所以，当且仅当时等号成立.

即成立.