人教版八年级上册12.1 全等三角形导学案

这是一份人教版八年级上册12.1 全等三角形导学案，共9页。


课首沟通
直角三角形全等的判定,一般三角形的全等的判定定理都有哪些?你喜欢哪一种?使用的时候有什么不同?
课首小测
[单选题] 如图，AB=AD，BC=CD，那么全等三角形的对数是（）
A.1B.2C.3D.4
（2015年江西南昌中考试题） 如图，OP平分∠MON , PE⊥OM于E,PF⊥ON于F,OA=OB, 则图中有 对全等三角形.
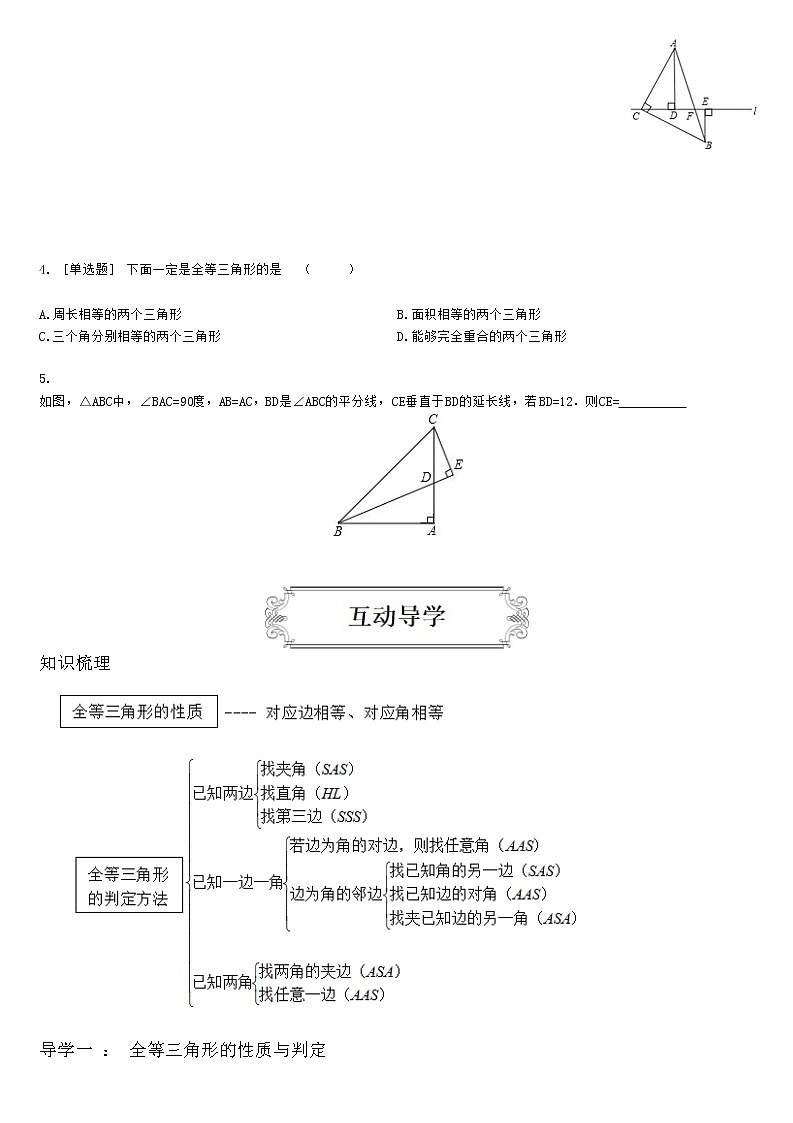
如图，将等腰直角三角形ABC的直角顶点置于直线l上，且过A，B两点分别作直线l的垂线，垂足分别为D，E，请你在图中找出一对全等三角形，并写出证明它们全等的过程．
学生姓名
年级
学科
授课教师
日期
时段
核心内容
全等三角形的性质与判定
课型
一对一
教学目标
1、掌握全等三角形的性质
2、会运用性质进行全等三角形的判定
3、掌握全等三角形性质与判定的综合运用
重、难点
重点:全等三角形的判定定理的灵活应用
难点:全等三角形的性质以及判定的综合运用
[单选题] 下面一定是全等三角形的是（）
A.周长相等的两个三角形B.面积相等的两个三角形
C.三个角分别相等的两个三角形D.能够完全重合的两个三角形
5.
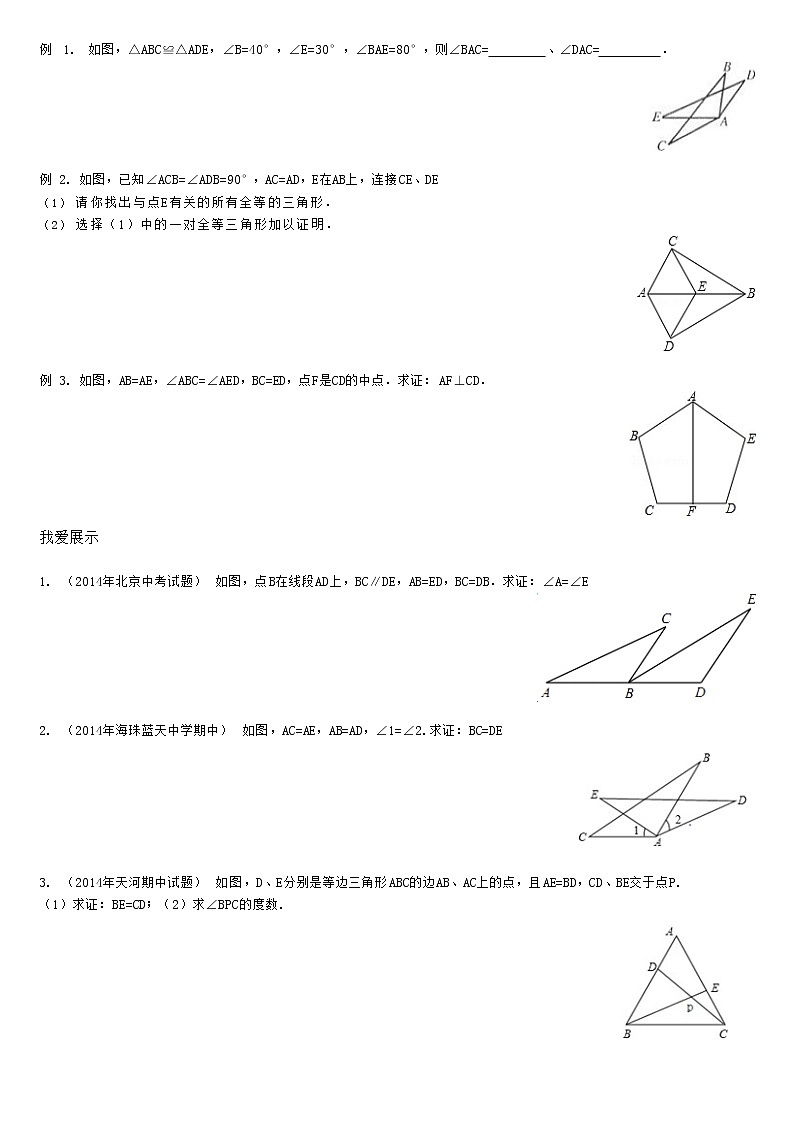
如图，△ABC中，∠BAC=90度，AB=AC，BD是∠ABC的平分线，CE垂直于BD的延长线，若BD=12．则CE=
知识梳理
导学一 ： 全等三角形的性质与判定
例 1. 如图，△ABC≌△ADE，∠B=40°，∠E=30°，∠BAE=80°，则∠BAC= 、∠DAC= ．
例 2. 如图，已知∠ACB=∠ADB=90°，AC=AD，E在AB上，连接CE、DE
请你找出与点E有关的所有全等的三角形．
选择（1）中的一对全等三角形加以证明．
例 3. 如图，AB=AE，∠ABC=∠AED，BC=ED，点F是CD的中点．求证：AF⊥CD．
我爱展示
（2014年北京中考试题） 如图，点B在线段AD上，BC∥DE，AB=ED，BC=DB．求证：∠A=∠E
（2014年海珠蓝天中学期中） 如图，AC=AE，AB=AD，∠1=∠2.求证：BC=DE
（2014年天河期中试题） 如图，D、E分别是等边三角形ABC的边AB、AC上的点，且AE=BD，CD、BE交于点P.
（1）求证：BE=CD；（2）求∠BPC的度数.
导学二 ： 倍长中线
例 1. （2015年十堰市初二期中考试） 如图，△ABC中，D为BC的中点．
求证：AB+AC＞2AD；
若AB=5，AC=3，求AD的取值范围．
例 2. 如图，在△ABC中，AD交BC于点D，点E是BC中点，EF∥AD交CA的延长线于点F，交EF于点G，若BG=CF，求证：AD为
△ABC的角平分线.
例 3. （2015年上海市初二期末考试） 已知在△ABC中，AD是BC边上的中线，E是AD上一点，且BE=AC，延长BE交AC于F， 求证：AF=EF。
我爱展示
阅读下面的题目及分析过程，并按要求进行证明．
已知：如图，E是BC的中点，点A在DE上，且∠BAE=∠CDE． 求证：AB=CD．
如图已知△ABC，AD是BC边上的中线，分别以AB边、AC边为直角边各向形外作等腰直角三角形， 求证:EF＝2AD
（2015年广州市初二月考试题） 已知：如图，在中， ，D、E在BC上，且DE=EC，过D作 交AE 于点F，DF=AC.求证：AE平分 。
导学三 ： 角平分线的性质
例 1. 如图，DB是△ABC的高，AE是角平分线，∠BAE=26°，求∠BFE的度数．
例 2. 已知：如图，BP，CP是△ABC的外角平分线，证明：点P一定在∠BAC的角平分线上．
例 3. 等边三角形ABC中，点E在AB上，点F在AC上 EDF=45 ，DB=DC，BDC=120 。请问现在EF、BE、CF有什么数量关系？并证明
我爱展示
1. （2014年惠州市期末试题） 已知，Rt△ABC中，∠C=90°，AC=BC，AD平分∠BAC.求证：AC+ CD =AB
2. 如图，在△ABC中，∠C＝2∠B，∠1＝∠2.求证：AB=AC+CD.
3. 如图，已知△ABC是等边三角形，∠BDC＝120º，说明AD=BD+CD的理由
导学四 ： 全等三角形的综合应用
例 1. 已知：如图，AC平分∠BAD，CE⊥AB与点E，CF⊥AD与点F，且BC=DC，你能说出BE与DF的数量关系吗？为什么？
例 2. 在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．
当直线MN绕点C旋转到图1的位置时，求证：①△ADC≌△CEB；②DE=AD+BE；
当直线MN绕点C旋转到图2的位置时，求证：DE=AD﹣BE；
当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明．
我爱展示
1. 如图，AD是的角平分线，H，G分别在AC，AB上，且HD＝BD.
求证：∠B与∠AHD互补；
若∠B＋2∠DGA＝180°，请探究线段AG与线段AH、HD之间满足的等量关系，并加以证明.
限时考场模拟 ： 15分钟
[单选题] （2015年江苏泰州中考试题） 如图，△中，AB=AC，D是BC的中点，AC的垂直平分线分别交 AC、AD、
AB于点E、O、F，则图中全等的三角形的对数是()
A.1对B.2对C.3对D.4对
（2015年江苏无锡中考试题） 已知：如图，AB∥CD，E是AB的点，CE=DE．求证： (1）∠AEC=∠BED；
(2）AC=BD．
如图，∠A=90°，∠D=90°，AC与BD相交于点E，BE=EC． 求证：△ABC≌△DCB．
如图，△EFG的三条边相等，三个内角也相等，且EH=FI=GJ，找出图中一对全等三角形，并说明理由．
（2014年广州市白云区期末试题） 如图，已知在△ABC中，AB=AC，∠A=100°，CD是∠ACB的平分线．求证： BC=CD+AD．
课后作业
[单选题] 如图所示是两个全等三角形，由图中条件可知，∠α=（）
A．65°B．30°C．85°D．30°或65°
已知：∠B=∠C，AD是△BAC的角平分线，DE⊥AB于E，DF⊥AC于F． 求证：BE=CF．
[单选题] （2014年广西） 下列命题：①有两个角和第三个角的平分线对应相等的两个三角形全等；②有两条边和第三条边上的中线对应相等的两个三角形全等；③有两条边和第三条边上的高对应相等的两个三角形全等．其中正确的是
（）
A．①②B．②③C．①③D．①②③
如图，已知Rt△ABC≌Rt△ADE，∠ABC=∠ADE=90°，BC与DE相交于点F，连接CD，EB．请你找出图中的一对全等三角形，并证明它．
已知CD是经过∠BCA顶点C的一条直线，CA=CB。E、F分别是直线CD上两点（不重合），且∠BEC＝∠CFA＝∠α。
若直线CD经过∠BCA的内部，且E、F在射线CD上，请解决下面问题：
①若∠BCA＝90°，∠α＝90°，请在图1中补全图形，并证明：BE=CF，EF＝|BE -AF|；
②如图2，若0°＜∠BCA＜180°，∠α+∠BCA＝180°，求证 △BCE≌△CAF。
如图3，若直线CD经过∠BCA的外部，∠α＝∠BCA，试探究EF、BE、AF三条线段数量关系，并证明．
如图,在△ABC中,分别以AB、AC为边,向△ABC外作正三角形、正四边形、正五边形,BE、CD相交于点O。
如图甲,求证: △ABE≌△ADC；
探究:如图甲,∠BOC的度数为 ； 如图乙, ∠BOC的度数为 ；
如图丙, ∠BOC的度数为 ；
1、总结一下本节课的重难点知识
2、完成老师规定的作业，制定相应的学习安排
3、做好下一阶段的学习笔记