人教版八年级上册13.1.1 轴对称教案设计

这是一份人教版八年级上册13.1.1 轴对称教案设计，共20页。

课首沟通
上讲回顾（错题管理）；作业检查。
课首小测
[单选题] [全等三角形的判定] [难度： ★★ ] 如图，已知∠ABC=∠BAD，添加下列条件还不能判定△ABC≌△BAD的是（)
A．AC=BDB．∠CAB＝∠DBAC．∠C＝∠DD．BC=AD
【参考答案】A
【题目解析】∵∠ABC=∠BAD,AB=AB，∠CAB=∠DBA，
∴△ABC≌△BAD（ASA）．所以选项B可以判定△ABC≌△BAD．∵∠ABC=∠BAD,∠C=∠D，AB=AB，
∴△ABC≌△BAD（AAS），所以选项C可以判定△ABC≌△BAD．∵BC=AD,∠ABC=∠BAD，AB=AB，
∴△ABC≌△BAD（SAS），
所以选项D可以判定△ABC≌△BAD．故此题选A．
[单选题] [角平分线的性质] [难度： ★★ ]如图，OP平分∠AOB，PA⊥OA于A，PB⊥OB于B，下列结论不一定成立的是（）
A．PA=PBB．PO平分∠APBC．OA=OBD．AB垂直平分OP
【参考答案】D
学生姓名
年级
学科
授课教师
日期
时段
核心内容
①轴对称的性质 ②垂直平分线的性质
课型
一对一
教学目标
1、了解轴对称、轴对称图形的概念，掌握轴对称图形的性质；
2、能画出简单平面图形关于给定对称轴的对称图形，在平面直角坐标系中，以坐标系为对称轴，能写出一个已知图形的坐标顶点，并知道对应顶点坐标之间的关系。
3、理解并掌握垂直平分线的概念和性质；
重、难点
1、准确掌握轴对称图形和关于直线成轴对称这两个概念的实质。
2、理解并掌握垂直平分线的概念和性质
【题目解析】
∵点E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，
[单选题] [全等三角形的判定与性质] [难度： ★★ ] 如图∠E=∠F=90°，∠B=∠C，AE=AF，给出下列结论：
①∠1=∠2；②BE=CF；③△ACN≌△ABM；④CD=DN． 其中正确的结论有（）
A．1个B．2个C．3个D．4个
【参考答案】C
【题目解析】根据三角形的内角和定理求出∠EAB=∠FAC，即可判断①；根据AAS证△EAB≌△FAC，即可判断②；推出
AC=AB，根据ASA即可证出③；不能推出CD和DN所在的三角形全等，也不能用其它方法证出CD=DN． 解：∵∠E=∠F=90°，∠B=∠C，
∵∠E+∠B+∠EAB=180°，∠F+∠C+∠FAC=180°，
∴∠EAB=∠FAC，
∴∠EAB﹣CAB=∠FAC﹣∠CAB， 即∠1=∠2，∴①正确；
在△EAB和△FAC中
∴△EAB≌△FAC，
∴BE=CF，AC=AB，∴②正确； 在△ACN和△ABM中
∴△ACN≌△ABM，∴③正确；
∵根据已知不能推出CD=DN，∴④错误；
∴正确的结论有3个， 故选C．
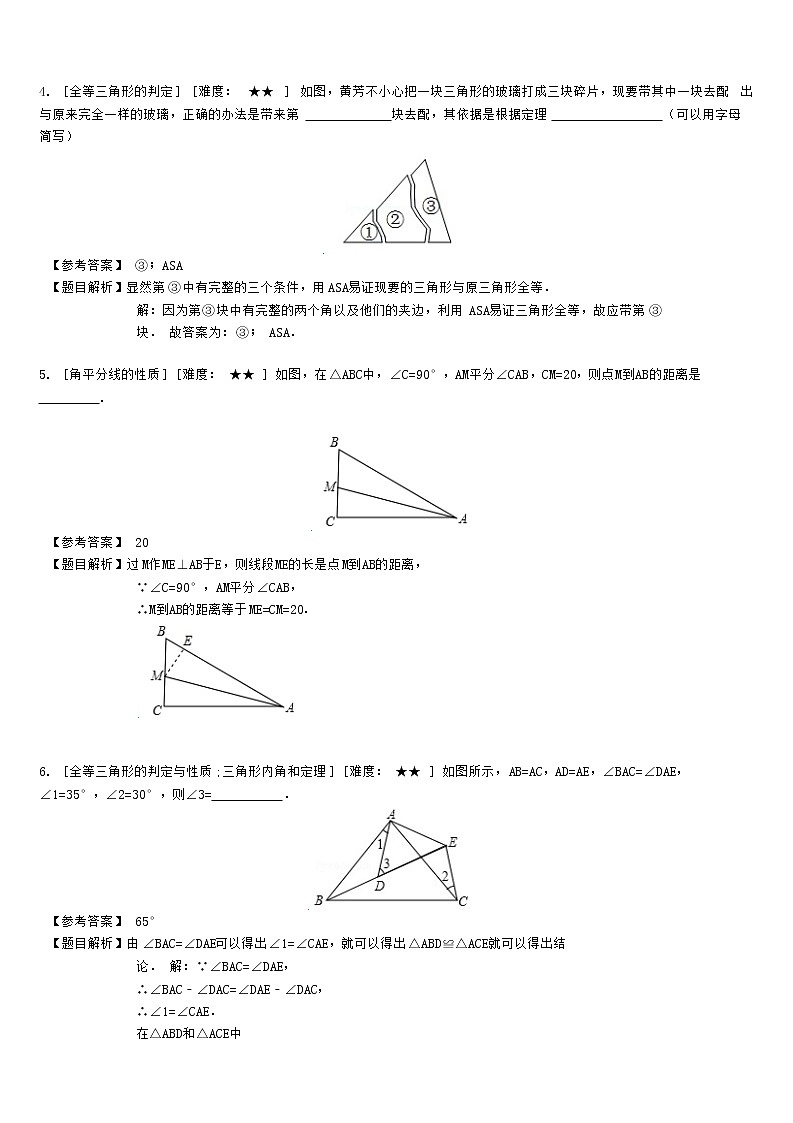
[全等三角形的判定] [难度： ★★ ] 如图，黄芳不小心把一块三角形的玻璃打成三块碎片，现要带其中一块去配出与原来完全一样的玻璃，正确的办法是带来第 块去配，其依据是根据定理 （可以用字母简写）
【参考答案】 ③；ASA
【题目解析】显然第③中有完整的三个条件，用ASA易证现要的三角形与原三角形全等．
解：因为第③块中有完整的两个角以及他们的夹边，利用ASA易证三角形全等，故应带第③块． 故答案为：③； ASA．
[角平分线的性质] [难度： ★★ ] 如图，在△ABC中，∠C=90°，AM平分∠CAB，CM=20，则点M到AB的距离是
.
【参考答案】 20
【题目解析】过M作ME⊥AB于E，则线段ME的长是点M到AB的距离，
∵∠C=90°，AM平分∠CAB，
∴M到AB的距离等于ME=CM=20．
[全等三角形的判定与性质;三角形内角和定理] [难度： ★★ ] 如图所示，AB=AC，AD=AE，∠BAC=∠DAE，
∠1=35°，∠2=30°，则∠3= ．
【参考答案】 65°
【题目解析】由∠BAC=∠DAE可以得出∠1=∠CAE，就可以得出△ABD≌△ACE就可以得出结论． 解：∵∠BAC=∠DAE，
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC，
∴∠1=∠CAE．
在△ABD和△ACE中
∴△ABD≌△ACE（SAS），
∴∠ABD=∠2=30°．
∵∠3=∠1+∠ABD，
∴∠3=35°+30°=65°．
故答案为：65°．
[全等三角形的判定] [难度： ★★ ] 如图，在△AEC和△DBF中，∠E＝∠F，点A、B、C、D在同一条直线上， AB＝
CD、CE∥BF. 求证：△AEC≌△DBF。
【参考答案】
[全等三角形的判定与性质] [难度： ★★ ] 如图，在△ABC和△ABD中，AC与BD相交于点E，AD=BC，∠DAB=∠CBA， 求证：AC=BD．
【参考答案】在△ADB和△BAC中，
∴△ADB≌△BAC（SAS），
∴AC=BD．
导学一 ：轴对称、轴对称图形知识点讲解
1、如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形；这条直线就是它的对称 轴．
2、把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线对称．折叠后重 合的点是对应点，叫做对称点．
3、轴对称的性质：
关于某条直线对称的两个图形是全等的；
如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线； 轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线．
例题
[单选题] [图形的对称] [难度： ★★ ] 下列图形中，不是轴对称图形的是（）
A.B.C.D.
【参考答案】A
【题目解析】解：A、不是轴对称图形，故本选项正确；
B、是轴对称图形，故本选项错误；
C、是轴对称图形，故本选项错误；
D、是轴对称图形，故本选项错误． 故选A．
[图形的对称] [难度： ★★ ] 请分别画出下图中各图的所有对称轴．
（1）正方形（2）正三角形（3）相交的两个圆
【参考答案】
[轴对称的性质;全等三角形的性质] [难度： ★★ ] 如图，△ABC与△A′B′C′关于直线l对称，则∠C′的度数为 ．
【参考答案】20°
【题目解析】∵△ABC与△A′B′C′关于直线l对称，
∴∠A′=∠A=50°，
在△A′B′C′中，∠C′=180°﹣∠A′﹣∠B′
=180°﹣50°﹣110°
=20°．
故答案为：20°．
[图形的对称] [难度： ★★ ] 小强站在镜前，从镜子中看到镜子对面墙上挂着的电子表，其读数如图所示，则电子表的实际时刻是 ．
【参考答案】10：21
[单选题] [图形的对称] [难度： ★★ ] 如图所示的矩形纸片，先沿虚线按箭头方向向右对折，接着将对折后的纸片沿虚线剪下一个小圆和一个小三角形，然后将纸片打开是下列图中的哪一个（）
A.B.C.D.
【参考答案】C
[单选题] [翻折变换（折叠问题）] [难度： ★★ ] 如图，将矩形纸片ABCD （图①）按如下步骤操作：（1）以过点A的直线为折痕折叠纸片，使点B恰好落在AD边上，折痕与BC边交于点E （如图②）；（2）以过点E的直线为折痕折叠纸片，使点A落在BC边上，折痕EF交AD边于点F （如图③）； （3）将纸片收展平，那么∠AFE的度数为（ ）
A．60°B．67.5°C．72°D．75°
【参考答案】B
我爱展示
[单选题] [图形的对称] [难度： ★★ ] 在以下的几何图形中，一定是轴对称图形的有 （）
A.2个B.3个C.4个D.5个
【参考答案】D
[图形的对称] [难度： ★★ ] 如图，是从镜中看到的一串数字，这串数字应为 ．
【参考答案】810076
[翻折变换（折叠问题）] [难度： ★★ ] 如图，Rt△ABC中，∠B=90°，AB=3cm，BC=4cm，将△ABC折叠，使点C与A 重合，得折痕DE，则△ABE的周长等于
【参考答案】7cm
【题目解析】 由轴对称的性质知，AE=CE，
∴△ABE的周长=AB+BE+AE=AB+BE+CE=AB+BC=3+4=7cm．
故答案为：7cm．
[翻折变换（折叠问题）] [难度： ★★ ] 如图a是长方形纸带，∠BFE=15°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数是 ．
【参考答案】135°
【题目解析】解：如图，
延长AE到H，由于纸条是长方形，
∴EH∥GF，
∴∠1=∠EFG，
根据翻折不变性得∠1=∠2，
∴∠2=∠EFG，
又∵∠DEF=15°，
∴∠2=∠EFG=15°，
∠FGD=15°+15°=30°．
在梯形FCDG中，
∠GFC=180°﹣30°=150°，
根据翻折不变性，∠CFE=∠GFC﹣∠GFE=150°﹣15°=135°．
导学二 ：线段的垂直平分线知识点讲解
1、经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线．
三角形三条边的垂直平分线交于一点，这一点到三角形三个顶点的距离相等．
2、垂直平分线的性质：线段垂直平分线上的点与这条线段两个端点的距离相等． 几何语言：
∵PQ是AB的垂直平分线
∴PA=PB
3、垂直平分线的判定：与一条线段两个端点距离相等的点，在这条线段的垂直平分线上． 几何语言：
∵PA=PB
∴P点在AB的垂直平分线上
例题
[线段垂直平分线的性质] [难度： ★★ ] 如图，已知M点分别到A、B的距离相等。N点分别到A、B的距离相等。 求证：MN垂直平分线段AB。
【参考答案】∵M点分别到A、B的距离相等，
∴M点在AB的垂直平分线上；
又∵N点分别到A、B的距离相等，
∴N点在AB的垂直平分线上； 所以MN垂直平分线段AB；
[三角形内角和定理;线段垂直平分线的性质] [难度： ★★ ] 如图，在△ABC中，AB＝AC，∠A＝40°，AB的垂直平分线交AB于点D，交AC于点E，连接BE，则∠CBE的度数为 ．
【参考答案】30°
【题目解析】因为AB＝AC，∠A＝40°，所以∠ABC＝∠C=70°,又DE垂直平分AB，所以AE=BE,所以∠ABE＝∠A=40°,所 以∠CBE=∠ABC-∠ABE=70°-40°=30°．
[线段垂直平分线的性质] [难度： ★★ ] △ABC中，DE是AC的垂直平分线，AE＝3cm，△ABD的周长为13cm，求△ABC 的周长。
【参考答案】19cm.
【题目解析】解：∵DE是AC的垂直平分线，AE=3cm，
∴AD=CD，AC=2AE=2×3=6cm，
∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC=13cm，
∴△ABC的周长=AB+BC+AC=13+6=19cm．
[线段垂直平分线的性质] [难度： ★★ ]已知：线段AB． 求作：线段AB的垂直平分线MN．
(要求：不写作法，但要保留作图痕迹，并写出结论)
【参考答案】 解：如图，MN即为线段AB的垂直平分线
[线段垂直平分线的性质] [难度： ★★ ] 如图，在△ABC中，DM、EN分别垂直平分AC和BC，交AB于M、N两点，DM与
EN相交于点F．
若△CMN的周长为15cm，求AB的长；
若∠MFN=70°，求∠MCN的度数．
【参考答案】（1）15cm;（2）40°
【题目解析】（1）∵DM、EN分别垂直平分AC和BC，
∴AM=CM，BN=CN，
∴△CMN的周长=CM+MN+CN=AM+MN+BN=AB，
∵△CMN的周长为15cm，∴AB=15cm；
（2）∵∠MFN=70°，∴∠MNF+∠NMF=180°﹣70°=110°，
∵∠AMD=∠NMF，∠BNE=∠MNF，∴∠AMD+∠BNE=∠MNF+∠NMF=110°，
∴∠A+∠B=90°﹣∠AMD+90°﹣∠BNE=180°﹣110°=70°，
∵AM=CM，BN=CN，∴∠A=∠ACM，∠B=∠BCN，
∴∠MCN=180°﹣2（∠A+∠B）=180°﹣2×70°=40°．
我爱展示
[线段垂直平分线的性质] [难度： ★★ ] 如图，AB=AC，MB=MC．直线AM是线段BC的垂直平分线吗？若是，请证明； 若不是，请说明理由。
【参考答案】是。证明如下：
∵AB=AC，MB=MC
∴点A在BC的垂直平分线上； 又∵MB=MC，
∴点M在BC的垂直平分线上；
∴直线AM是线段BC的垂直平分线。
[单选题] [线段垂直平分线的性质] [难度： ★★ ]如图，在Rt△ABC中，∠B=90°，ED是AC的垂直平分线，交AC 于点D，交BC于点E．已知∠BAE=10°，则∠C的度数为（）
A.30°B.40°C.50°D.60°
【参考答案】B
[线段垂直平分线的性质] [难度： ★★ ] 如图，△ABC的周长为19cm，AC的垂直平分线DE交BC于D，E为垂足，AE=3cm，则△ABD的周长为 cm．
【参考答案】13
【题目解析】∵AC的垂直平分线DE交BC于D，E为垂足
∴AD=DC，AC=2AE=6cm，
∵△ABC的周长为19cm，
∴AB+BC=13cm
∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC=13cm．
[线段垂直平分线的性质] [难度： ★★ ] 现要在三角地ABC内建一中心医院，使医院到A、B两个居民小区的距离相等，并且到公路AB和AC的距离也相等，请确定这个中心医院的位置．
【参考答案】 解：如图，P为这个中心医院的位置。
导学三 ： 轴对称变换例题
[图形的对称] [难度： ★★ ] 如图是一个图案的一半，其中虚线是这个图案的对称轴，请你画出这个图案的另一半．
【参考答案】解：
[轴对称的性质] [难度： ★★ ]已知：如图，A、B两点在直线l的同侧，点A'与A关于直线l对称，连接A'B交l于
P点，若A'B＝a.
求AP＋PB；
若点M是直线l上异于P点的任意一点，求证：AM＋MB＞AP＋PB．
【参考答案】1)解:∵点A和A'关于直线L对称.
∴AP=A'P,故AP+PB=A'P+PB=A'B=a.
故AP+PB值为a.
(2)证明:∵点A和A'关于直线L对称.
∴AP=A'P;AM=A'M.
则AP+PB=A'P+PB=A'B;AM+MB=A'M+MB.
∵A'M+MB>A'B.(三角形两边之和大于第三边)
∴A'M+MB>AP+PB.(等量代换)
3. [图形的对称] [难度： ★★ ] 如图，△ABC的顶点分别为A(2,4),B(-2,2),C(3,1)，
作出△ABC关于x轴对称的图形△DEF，写出顶点D、E、F的坐标.
如果点H(3m-1,n-6)与点H'(2n+7,3m-9)关于y轴对称，求m,n的值.
【参考答案】解：（1）如图：D（2，-4），E（-2，-2），F（3，-1）.
(2)m的值为0，n的值为-3.
我爱展示
[图形的对称] [难度： ★★ ] 画出所示图形关于直线L的对称图形．
【参考答案】
[图形的对称] [难度： ★★ ] 请在下列三个2×2的方格中，各画出一个三角形，要求所画三角形是图中三角形经过轴对称变换后得到的图形，且所画的三角形顶点与方格中的小正方形顶点重合，并将所画三角形涂上阴影．（注：所画 的三个图形不能重复）
【参考答案】解：
[图形的对称] [难度： ★★ ] 如图，在平面直角坐标系中， ， ， ．
（1）求出的面积．
【参考答案】1）7.5(2)如图
(3) 的坐标分别是(1，5)、（1，0）、（4，3）
限时考场模拟 ：15min
[单选题] [图形的对称] [难度： ★★ ] 如图，下列图案是我国几家银行的标志，其中是轴对称图形的有（
）
A、1个B、2个C、3个D、4个
【参考答案】C
[图形的对称] [难度： ★★ ]图是从镜中看到的一串数字，这串数字应为
【参考答案】 3265
（2）在图中作出
关于
轴的对称图形
．
（3）写出点
的坐标
[单选题] [图形的对称] [难度： ★★ ] 如图，把一个正方形三次对折后沿虚线剪下，则所得图形大致是（
）
C.
B.D.
【参考答案】A
[单选题] [线段垂直平分线的性质] [难度： ★★ ] 如图，直线L是一条河，P，Q是两个村庄．欲在L上的某处修建一个水泵站，向P，Q两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是（）
A.B.C.D.
【参考答案】D
[线段垂直平分线的性质;三角形内角和定理;三角形] [难度： ★★ ] ΔABC中，AB＝AC，AB的垂直平分线交AC于P 点．
（1）若∠A＝35°，则∠BPC＝ ；
（2）若AB＝5 cm，BC＝3 cm，则ΔPBC的周长＝ ．
【参考答案】（1）37.5°；（2）8cm
[线段垂直平分线的性质] [难度： ★★ ]如图：点P为∠AOB内一点，分别作出P点关于OA、OB的对称点P1，P2，连接P1P2交OA于N，交OB于M，P1P2=15，则△PMN的周长为 .
【参考答案】15
【题目解析】 根据对称的性质可得：P1M=PM，P2N=PN，
∴△PMN的周长=PM+MN+PN
=P1M+MN+P2N
=P1P2
=15
[图形的对称] [难度： ★★ ] 作图：已知四边形ABCD和直线，画出与四边形ABCD关于直线h的对称图形（保留作图痕迹）
【参考答案】如图所示；
[线段垂直平分线的性质] [难度： ★★ ] 在△ABC中， EM、NF分别垂直平分AB和AC，交AB于M、N两点．
（1）若BC = 10 cm，试求△AMN的周长．
（2）在△ABC中，AB = AC，∠BAC= 100°，求∠MAN的度数．
（3） 在 (2) 中，若无AB = AC的条件，你还能求出∠MAN的度数吗？若能，请求出；若不能，请说明理由．
【参考答案】（1） cm
（2）
（3） 能，证明如下：
∵ MA = MB
∴ ∠MAB =∠B
∵ NA = NB
∴ ∠NAC =∠C
∴
【题目解析】(1) ∵ ME垂直平分AB
∴ MA = MB
∵ NF垂直平分AC
∴ NA = NC
∴cm
(2) ∵ AB = AC，
∴
∵ MA = MB
∴
∵ NA = NC
∴
∴
课后作业
[单选题] [图形的对称] [难度： ★★ ] 下列图形中一定是轴对称图形的是（）
A.梯形B.直角三角形C.角D.平行四边形
【参考答案】C
[单选题] [图形的对称] [难度： ★★ ] 已知点P关于x轴的对称点为（a，－2），关于y轴对称点为（1，b），那么点P的坐标为（）
A．（a，－b）B．（b，－a）C．（－2，1）D．（－1，2）
【参考答案】D
[单选题] [图形的对称] [难度： ★★ ] 李芳同学球衣上的号码是253，当他把镜子放在号码的正前方时，镜子中的号码是（）
A. B. C. D.
【参考答案】A
[单选题] [线段垂直平分线的性质] [难度： ★★ ] 如图：DE是△ABC中AC边的垂直平分线，若BC=8厘米，AB=10厘米，则△EBC的周长为（ ）厘米
A.16B.18C.26D.28
【参考答案】B
[单选题] [线段垂直平分线的性质] [难度： ★★ ] 在联欢晚会上，有A、B、C三名同学站在一个三角形的三个顶点位置上，他们在玩抢凳子游戏，要求在他们中间放一个木凳，谁先抢到凳子谁获胜，为使游戏公平，则凳子应放的 最适当的位置在△ABC的（ ）
A．三边中线的交点B．三条角平分线的交点C．三边上高的交点D．三边中垂线的交点
【参考答案】D
[作图-轴对称变换] [难度： ★★ ] 已知在平面直角坐标系中有三点A（-2，1）、B（3，1）、C（2，3）．请回答如下问题：
在坐标系内描出点A、B、C的位置;并求出△ABC的面积；
在平面直角坐标系中画出△A′B′C′,使它与△ABC 关于x轴对称,并写出顶点A’、B’、C’的坐标．
若M（x,y）是△ABC内部任意一点，请直接写出这点在△A′B′C′内部的对应点M＇的坐标．
【参考答案】（1）如图，面积为5；
（2）如图；A′（-2，-1）、B′（3，-1）、C′（2，-3）；
（3）M'（x，-y）．
【题目解析】（1）描点如图，
由题意得，AB∥x轴，且AB=3-（-2）=5，
∴S△ABC= ×5×2=5
（2）如图；A′（-2，-1）、B′（3，-1）、C′（2，-3）；
（3）M'（x，-y）．
[线段垂直平分线的性质;角平分线的性质] [难度： ★★ ] 如图所示，AD是△ABC的角平分线，EF是AD的垂直平分线，交BC的延长线于点F，连接AF．求证：∠BAF=∠ACF
【参考答案】
证明：∵EF是AD的垂直平分线，
∴AF=DF，
∴∠FAD=∠ADF，
∵∠FAD=∠FAC+∠CAD，∠ADF=∠B+∠DAB，
∴AD是∠BAC的平分线，
∴∠DAB=∠CAD，
∴∠CAF=∠B，
∴∠BAC+∠FAC=∠B+∠BAC， 即∠BAF=∠ACF．
[线段垂直平分线的性质;角平分线的性质;三角形] [难度： ★★★ ] 已知：如图， AF平分∠BAC，BC⊥AF， 垂足为E，点D与点A关于点E对称，PB分别与线段CF， AF相交于P，M．
求证：AB=CD；
若∠BAC=2∠MPC，请你判断∠F与∠MCD的数量关系，并说明理由．（提示：这题涉及等腰三角形的性质，请先预习下 一次课的内容再完成）
【参考答案】（1）证明：∵AF平分∠BAC，
∴∠CAD=∠DAB= ∠BAC，
∵D与A关于E对称，
∴E为AD中点，
∵BC⊥AD，
∴BC为AD的中垂线，
∴AC=CD．
在Rt△ACE和Rt△ABE中，（注：证全等也可得到AC=CD）
∠CAD+∠ACE=∠DAB+∠ABE=90°，∠CAD=∠DAB，
∴∠ACE=∠ABE，
∴AC=AB（注：证全等也可得到AC=AB），
∴AB=CD．
（2）解：∠F=∠MCD，理由如下：
∵∠BAC=2∠MPC， 又∵∠BAC=2∠CAD，
∴∠MPC=∠CAD，
∵AC=CD，
∴∠CAD=∠CDA，
∴∠MPC=∠CDA，
∴∠MPF=∠CDM，
∵AC=AB，AE⊥BC，
∴CE=BE（注：证全等也可得到CE=BE），
∴AM为BC的中垂线，
∴CM=BM．（注：证全等也可得到CM=BM）
∵EM⊥BC，
∴EM平分∠CMB（等腰三角形三线合一）．
∴∠CME=∠BME（注：证全等也可得到∠CME=∠BME．），
∵∠BME=∠PMF，
∴∠PMF=∠CME，
∴∠MCD=∠F．（注：证三角形相似也可得到∠MCD=∠F）
1、花10~15min回顾课堂讲的内容，总结一下本节课所学的知识点；
2、完成老师规定的作业，制定相应的学习安排。
3、做好下一阶段的预习，做到下一讲“有备而来”