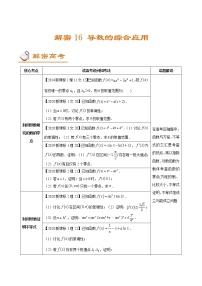
高中数学高考解密15 导数与函数的单调性、极值、（讲义）-【高频考点解密】2021年新高考数学二轮复习讲义+分层训练

这是一份高中数学高考解密15 导数与函数的单调性、极值、（讲义）-【高频考点解密】2021年新高考数学二轮复习讲义+分层训练，共11页。

核心考点一 导数的几何意义
1.导数的几何意义
函数f(x) 在x0处的导数是曲线f(x)在点P(x0，f(x0))处的切线的斜率，曲线f(x)在点P处的切线的斜率k＝f′(x0)，相应的切线方程为y－f(x0)＝f′(x0)(x－x0).
易错提醒 求曲线的切线方程时，要注意是在点P处的切线还是过点P的切线，前者点P为切点，后者点P不一定为切点.
2.四个易误导数公式
(1)(sin x)′＝cs x；
(2)(cs x)′＝－sin x；
(3)(ax)′＝axln a(a>0，且a≠1)；
(4)(lgax)′＝eq \f(1,xln a)(a>0，且a≠1，x>0).
1．【2020新课标1理6】函数的图像在点处的切线方程为（ ）
A． B． C． D．
【解析】，，，，因此所求切线的方程为，即．故选B．
2．【2018新课标1文6理5】设函数．若为奇函数，则曲线在点处的切线方程为( )
A．B．C．D．
【解析】解法一：因为函数为奇函数，所以，所以
，所以，因为，所以，所以，所以，所以，所以曲线在点处的切线方程为．故选D．
解法二：因为函数为奇函数，所以，所以
，解得，所以，
所以，所以，所以曲线在点处的切线方程为．故选D．
解法三：易知，因为为奇函数，所以函数
为偶函数，所以，解得，所以，所以，所以，所以曲线在点处的切线方程为．故选D．
3．【2020新课标1文15】曲线的一条切线的斜率为2，则该切线的方程为_____________．
【解析】设切线的切点坐标为，，所以切点坐标为，所求的切线方程为，即．故答案为．
1．【2020新课标3理10】若直线与曲线和都相切，则的方程为（ ）
A．B．C．D．
【解析】解法1：设直线在曲线上的切点为，则，
函数的导数为，则直线的斜率，
设直线的方程为，即，
由于直线与圆相切，则，
两边平方并整理得，解得或（舍），
则直线的方程为，即．故选D．
解法2：由原点到直线的距离为，排除BC；把代入得，而，排除A；把代入得，方程有唯一解，故选D．
2．【2020新课标3文15】设函数．若，则_________．
【解析】由函数的解析式可得，
则，据此可得，整理可得，解得．故答案．
3．【2016新课标2理16】若直线是曲线的切线，也是曲线的切线，则 ．
【解析】设与和的切点分别为 和．
则切线分别为，，
化简得，，
依题意，解得，从而．
核心考点二 利用导数研究函数的单调性
1.导数与函数单调性的关系.
①f′(x)>0是f(x)为增函数的充分不必要条件，如函数f(x)＝x3在(－∞，＋∞)上单调递增，但f′(x)≥0.
②f′(x)≥0是f(x)为增函数的必要不充分条件，如果函数在某个区间内恒有f′(x)＝0时，则f(x)为常数函数.
2.利用导数研究函数单调性的方法.
①若求单调区间(或证明单调性)，只要在函数定义域内解(或证明)不等式f′(x)>0或f′(x)0恒成立，∴m≥－eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,x)))eq \s\up12(2)＋eq \f(2,x).
令g(x)＝－eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,x)))eq \s\up12(2)＋eq \f(2,x)，则当eq \f(1,x)＝1，即x＝1时，函数g(x)取最大值1，故m≥1.故选C.
2.已知x＝1是f(x)＝2x＋eq \f(b,x)＋ln x的一个极值点.
(1)求函数f(x)的单调递减区间.
(2)设函数g(x)＝f(x)－eq \f(3＋a,x)，若函数g(x)在区间[1，2]内单调递增，求a的取值范围.
【解析】(1)f(x)＝2x＋eq \f(b,x)＋ln x，定义域(0，＋∞).
∴f′(x)＝2－eq \f(b,x2)＋eq \f(1,x)＝eq \f(2x2＋x－b,x2).
因为x＝1是f(x)＝2x＋eq \f(b,x)＋ln x的一个极值点，所以f′(1)＝0，即2－b＋1＝0.
解得b＝3，经检验，适合题意，所以b＝3.
所以f′(x)＝2－eq \f(3,x2)＋eq \f(1,x)＝eq \f(2x2＋x－3,x2)，令f′(x)0，右侧f′(x)eq \f(1,2)，则当x∈eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(1,a)，2))时，f′(x)0.
所以f(x)在x＝2处取得极小值.
若a≤eq \f(1,2)，则当x∈(0，2)时，x－20，则当时，；当时，．
故在单调递增，在单调递减；
若a=0，在单调递增；
若a0恒成立，
所以由f′(x)>0，得x>1；由f′(x)