高中数学高考精品解析：2020年全国统一高考数学试卷（文科）（新课标Ⅲ）（原卷版）

这是一份高中数学高考精品解析：2020年全国统一高考数学试卷（文科）（新课标Ⅲ）（原卷版），共6页。
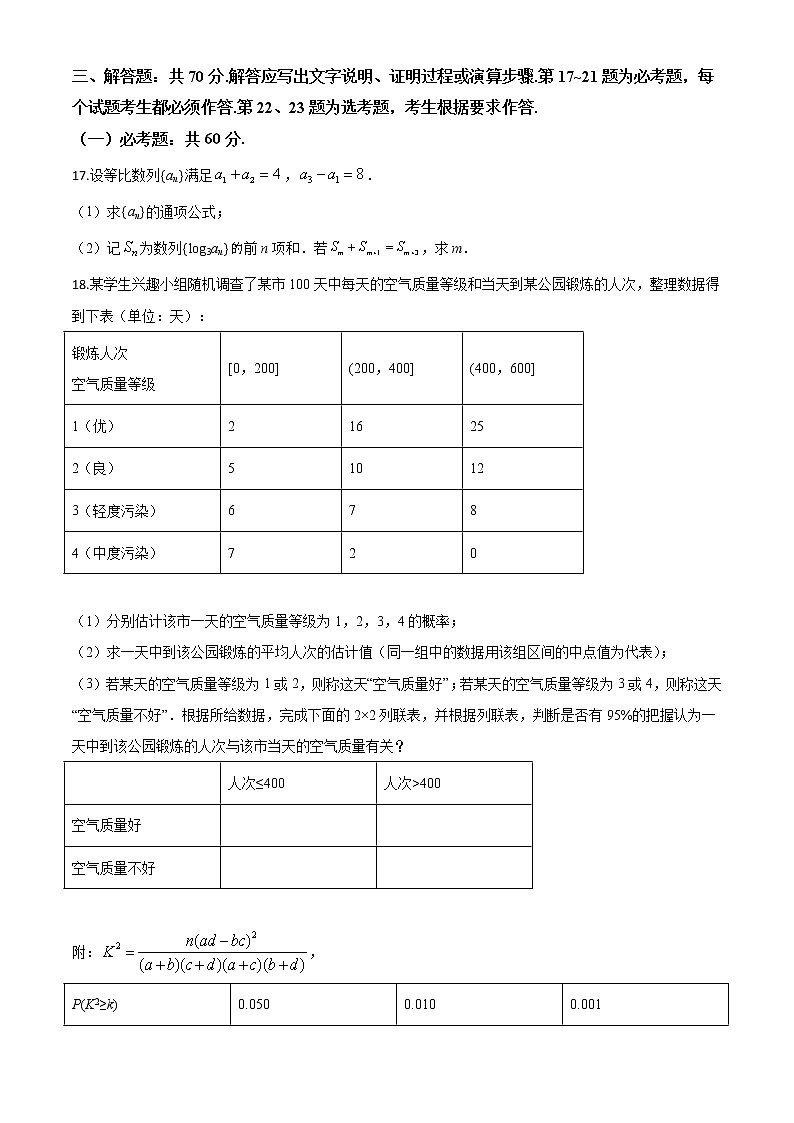
2020年普通高等学校招生全国统一考试文科数学注意事项：1．答卷前，考生务必将自己的姓名和准考证号填写在答题卡上.2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本试卷上无效.3．考试结束后，将本试卷和答题卡一并交回.一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合，，则A∩B中元素的个数为（    ）A. 2 B. 3 C. 4 D. 52.若，则z=（    ）A. 1–i B. 1+i C. –i D. i3.设一组样本数据x1，x2，…，xn的方差为0.01，则数据10x1，10x2，…，10xn的方差为（    ）A. 0.01 B. 0.1 C. 1 D. 104.Logistic模型是常用数学模型之一，可应用于流行病学领城．有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I(t)(t的单位：天)的Logistic模型：，其中K为最大确诊病例数．当I()=0.95K时，标志着已初步遏制疫情，则约为（    ）（ln19≈3）A 60 B. 63 C. 66 D. 695.已知，则（    ）A.  B.  C.  D. 6.在平面内，A，B是两个定点，C是动点，若，则点C的轨迹为（    ）A. 圆 B. 椭圆 C. 抛物线 D. 直线7.设为坐标原点，直线与抛物线C：交于，两点，若，则的焦点坐标为（    ）A.  B.  C.  D. 8.点(0，﹣1)到直线距离的最大值为（    ）A. 1 B.  C.  D. 29.下图为某几何体的三视图，则该几何体的表面积是（    ）A. 6+4 B. 4+4 C. 6+2 D. 4+210.设，，，则（    ）A.  B.  C.  D. 11.在△ABC中，cosC=，AC=4，BC=3，则tanB=（    ）A.  B. 2 C. 4 D. 812.已知函数f(x)=sinx+，则（    ）A. f(x)的最小值为2 B. f(x)的图像关于y轴对称C. f(x)的图像关于直线对称 D. f(x)的图像关于直线对称二、填空题：本题共4小题，每小题5分，共20分.13.若x，y满足约束条件 ，则z=3x+2y的最大值为_________．14.设双曲线C： (a>0，b>0)的一条渐近线为y=x，则C的离心率为_________．15.设函数．若，则a=_________．16.已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为_________．三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.（一）必考题：共60分.17.设等比数列{an}满足，．（1）求{an}的通项公式；（2）记为数列{log3an}前n项和．若，求m．18.某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次，整理数据得到下表（单位：天）：锻炼人次空气质量等级[0，200](200，400](400，600]1（优）216252（良）510123（轻度污染）6784（中度污染）720 （1）分别估计该市一天的空气质量等级为1，2，3，4的概率；（2）求一天中到该公园锻炼的平均人次的估计值（同一组中的数据用该组区间的中点值为代表）；（3）若某天的空气质量等级为1或2，则称这天“空气质量好”；若某天的空气质量等级为3或4，则称这天“空气质量不好”．根据所给数据，完成下面的2×2列联表，并根据列联表，判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关？ 人次≤400人次>400空气质量好  空气质量不好   附：，P(K2≥k)0.050  0.010 0.001k3.8416.63510.828  19.如图，长方体中，点，分别在棱，上，且，．证明：（1）当时，；（2）点在平面内．20.已知函数．（1）讨论的单调性；（2）若有三个零点，求取值范围．21.已知椭圆的离心率为，，分别为的左、右顶点．（1）求的方程；（2）若点在上，点在直线上，且，，求的面积．（二）选考题：共10分.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分.[选修4-4：坐标系与参数方程] 22.在直角坐标系xOy中，曲线C的参数方程为(t为参数且t≠1)，C与坐标轴交于A，B两点.（1）求||：（2）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，求直线AB的极坐标方程.[选修4-5：不等式选讲]23.设a，b，cR，a+b+c=0，abc=1．（1）证明：ab+bc+ca<0；（2）用max{a，b，c}表示a，b，c中的最大值，证明：max{a，b，c}≥．