高中数学高考考点24 章末检测四（原卷版）

这是一份高中数学高考考点24 章末检测四（原卷版），共5页。试卷主要包含了函数的图像大致为等内容，欢迎下载使用。
1、（2021·浙江高三其他模拟）函数在处的导数是（ ）
A．B．C．6D．2
2、（2021·陕西西安市·长安一中高三月考（文））曲线在处的切线方程为（ ）
A．B．
C．D．
3、（2021·淮北市树人高级中学高二期末（文））已知直线与曲线相切，则（ ）
A．1B．C．0D．
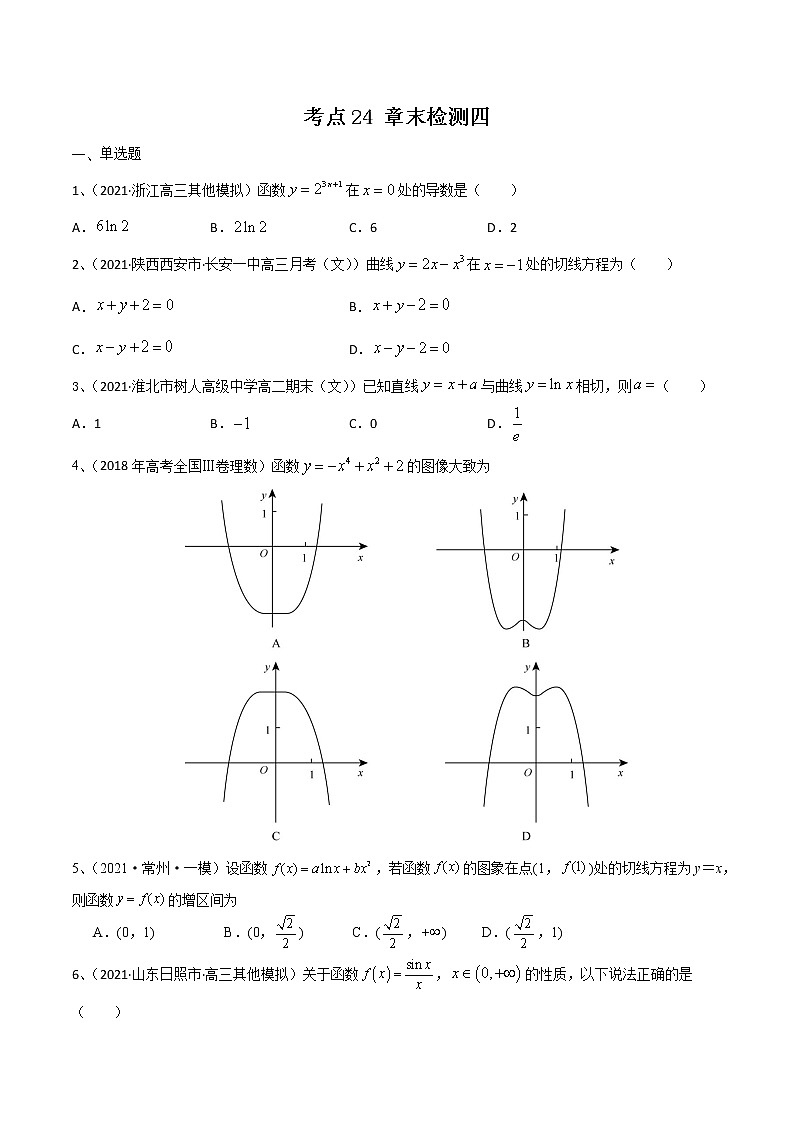
4、（2018年高考全国Ⅲ卷理数）函数的图像大致为
5、（2021·常州·一模）设函数，若函数的图象在点(1，)处的切线方程为y＝x，则函数的增区间为
A．(0，1) B．(0，) C．(，) D．(，1)
6、（2021·山东日照市·高三其他模拟）关于函数，的性质，以下说法正确的是（ ）
A．函数的周期是B．函数在上有极值
C．函数在单调递减D．函数在内有最小值
7、（湖南省常德市2021届高三模拟）若则（ ）
A．B．
C．D．
8、（2021·江苏扬州市高三模拟）已知定义在上的奇函数在上单调递减，且满足，则关于的不等式的解集为（ ）
A．B．
C．D．
多选题
9、（2020届山东师范大学附中高三月考）已知函数的定义域为且导函数为，如图是函数的图象，则下列说法正确的是
A．函数的增区间是，
B．函数的增区间是，
C．是函数的极小值点
D．是函数的极小值点
10、（2021·山东济南市·高三一模）已知函数的图象在处切线的斜率为，则下列说法正确的是（ ）
A．B．在处取得极大值
C．当时，D．的图象关于点中心对称
11、（2021·山东潍坊市·高三三模）已知函数，则下列结论正确的是（ ）
A．的周期为B．的图象关于对称
C．的最大值为D．在区间在上单调递减
12、（江苏省连云港市2021届高三调研）已知函数，则（ ）.
A．是奇函数B．
C．在单调递增D．在上存在一个极值点
三、填空题
13、（2021·山东德州市·高三期末）已知直线是曲线的一条切线，则_________．
14、（2021·江苏省新海高级中学高三期末）在平面直角坐标系中，是曲线（）上的一个动点，则点到直线的距离的最小值是________．
15、（2021·山东青岛市·高三期末）设函数的图象在点处的切线为，若方程有两个不等实根，则实数的取值范围是__________．
16、（湖北省九师联盟2021届高三联考）已知函数，若且，则的最大值是___________.
四、解答题
17、（2021·山东济南市·高三一模）已知函数.若，求的最小值；
18、已知函数f (x)＝ax3＋x2(a∈R)在x＝－eq \f(4,3)处取得极值．
(1)求a的值；
(2)若g(x)＝f (x)ex，讨论g(x)的单调性．
19、（2021·山东烟台市·高三二模）已知函数在处的切线斜率为．
（1）确定的值，并讨论函数的单调性；
20、（2021·河北张家口市·高三期末）已知函数.
（1）当时，求曲线在处的切线方程；
（2）若，且在上的最小值为0，求的取值范围.
21、（2021·山东威海市·高三期末）已知函数.
（1）当时，求过点且与曲线相切的直线方程;
（2）若，求实数的取值范围.
22、（2021·河北唐山市高三三模）已知函数.
（1）求函数的单调区间；
（2）设，证明：.