北京东城区中考数学2020-2022三年模拟（一模、二模）按题型分层汇编-05填空题中档题

这是一份北京东城区中考数学2020-2022三年模拟（一模、二模）按题型分层汇编-05填空题中档题，共8页。试卷主要包含了分解因式，数学课上，李老师提出如下问题，1斗，价值10钱等内容，欢迎下载使用。
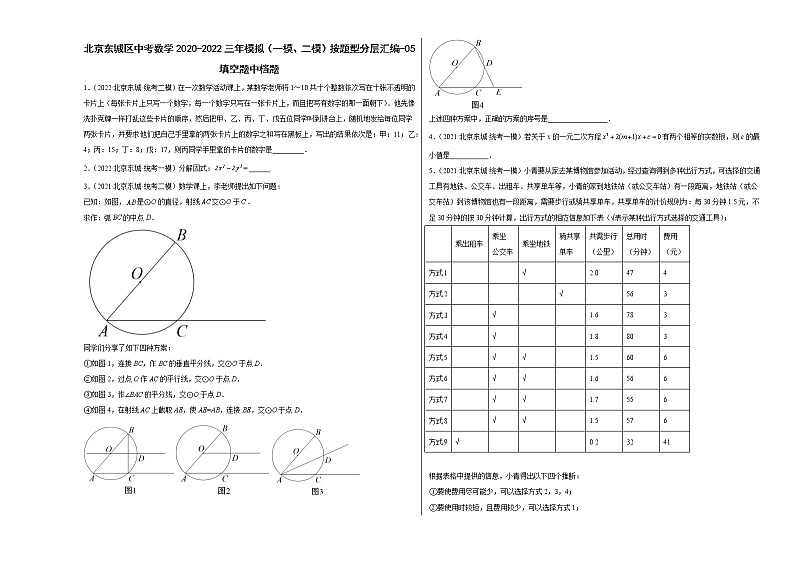
北京东城区中考数学2020-2022三年模拟（一模、二模）按题型分层汇编-05填空题中档题1．（2022·北京东城·统考二模）在一次数学活动课上，某数学老师将1～10共十个整数依次写在十张不透明的卡片上（每张卡片上只写一个数字，每一个数字只写在一张卡片上，而且把写有数字的那一面朝下）．他先像洗扑克牌一样打乱这些卡片的顺序，然后把甲、乙、丙、丁、戊五位同学叫到讲台上，随机地发给每位同学两张卡片，并要求他们把自己手里拿的两张卡片上的数字之和写在黑板上，写出的结果依次是：甲：11；乙：4；丙：15；丁：8；戊：17，则丙同学手里拿的卡片的数字是_________．2．（2022·北京东城·统考一模）分解因式：= ______.3．（2021·北京东城·统考二模）数学课上，李老师提出如下问题：已知：如图，是⊙O的直径，射线交⊙O于．求作：弧的中点D．同学们分享了如下四种方案：①如图1，连接BC，作BC的垂直平分线，交⊙O于点D．②如图2，过点O作AC的平行线，交⊙O于点D．③如图3，作∠BAC的平分线，交⊙O于点D．④如图4，在射线AC上截取AE，使AE=AB，连接BE，交⊙O于点D．上述四种方案中，正确的方案的序号是_________________．4．（2021·北京东城·统考一模）若关于x的一元二次方程有两个相等的实数根，则c的最小值是___________．5．（2021·北京东城·统考一模）小青要从家去某博物馆参加活动，经过查询得到多种出行方式，可选择的交通工具有地铁、公交车、出租车、共享单车等，小青的家到地铁站（或公交车站）有一段距离，地铁站（或公交车站）到该博物馆也有一段距离，需要步行或骑共享单车，共享单车的计价规则为：每30分钟1.5元，不足30分钟的按30分钟计算，出行方式的相应信息如下表（√表示某种出行方式选择的交通工具）； 乘出租车乘坐公交车乘坐地铁骑共享单车共需步行（公里）总用时（分钟）费用（元）方式1  √ 2.0474方式2   √ 563方式3 √  1.6783方式4 √  1.8803方式5 √√ 1.5606方式6 √√ 1.6566方式7 √√ 1.7556方式8 √√ 1.5576方式9√   0.23241 根据表格中提供的信息，小青得出以下四个推断：①要使费用尽可能少，可以选择方式2，3，4；②要使用时较短，且费用较少，可以选择方式1；③如果选择公交车和地铁混合的出行方式，平均用时约57分钟；④如果将上述出行方式中的“步行”改为“骑共享单车”，那么除方式2外，其它出行方式的费用均会超过8元．其中推断合理的是_______________（填序号）．6．（2021·北京东城·统考一模）用一组，的值说明命题“若，则”是错误的，这组值可以是____， ____7．（2020·北京东城·二模）在“中国汉字听写大赛”选拔赛中，甲、乙两位同学的平均分都是90分，甲同学成绩的方差是15，乙同学成绩的方差是3，由此推断甲、乙两人中成绩稳定的是_______．8．（2020·北京东城·统考一模）《九章算术》中有这样一个题：“今有醇酒一斗，直钱五十；行酒一斗，直钱一十．今将钱三十，得酒二斗．问醇、行酒各得几何？”其译文是：今有醇酒（优质酒）1斗，价值50钱；行酒（劣质酒）1斗，价值10钱．现有30钱，买得2斗酒．问醇酒、行酒各能买得多少？设醇酒为x斗，行酒为y斗，则可列二元一次方程组为_____．9．（2020·北京东城·统考一模）随机从1，2，3，4中任取两个不同的数，分别记为a和b，则a+b＞4的概率是_____．10．（2020·北京东城·统考一模）甲、乙两队参加了“端午情，龙舟韵”赛龙舟比赛，两队在比赛时的路程s（米）与时间t（秒）之间的函数图象如图所示，根据图象有以下四个判断：①乙队率先到达终点；②甲队比乙队多走了126米；③在47.8秒时，两队所走路程相等；④从出发到13.7秒的时间段内，甲队的速度比乙队的慢．所有正确判断的序号是_____．11．（2020·北京东城·统考一模）若x2+x﹣3＝0，则代数式2（x﹣2）（x+2）﹣x（x﹣1）的值是_____．12．（2020·北京东城·统考一模）从﹣1，0，2，3四个数中任取两个不同的数（记作ak，bk）构成一个数对Mk＝{ak，bk）（其中k＝1，2，…，s，且将{ak，bk}与{bk，ak}视为同一个数对），若满足：对于任意的Mi＝{ai，bi}和Mj＝{aj，bj）（i≠j，1≤i≤s，1≤j≤s）都有ai+bi≠aj+bj，则s的最大值是_____．13．（2020·北京东城·二模）如图，在中，AB的垂直平分线交A于点D，交BC于点E，若，，则的周长为________．
参考答案：1．5和10【分析】根据两数之和结果确定，对两个加数的不同情况进行分类讨论，列举出所有可能的结果后，再逐一根据条件进行推理判断，最后确定出正确结果即可．【详解】解：由题意可知，一共十张卡片十个数，五个人每人两张卡片，∴每人手里的数字不重复．由甲：11，可知甲手中的数字可能是1和10，2和9，3和8，4和7，5和6；由乙：4，可知乙手中的数字只有1和3；由丙：15，可知丙手中的数字可能是5和10，7和8，6和9；由丁：8，可知丁手中的数字可能是1和7，2和6，3和5；由戊：17，可知戊手中的数字可能是7和10，8和9；∴丁只能是2和6，甲只能是4和7，丙只能是5和10，戊只能是8和9．故答案为：5和10．【点睛】本题考查的是有理数加法的应用，关键是把所有可能的结果列举出来，再进行推理．2．【分析】先提取公因式2，再根据平方差公式进行二次分解即可求得答案．【详解】2x2-2y2=2（x2-y2）=2（x+y）（x-y）．故答案为2（x+y）（x-y）．【点睛】本题考查了提公因式法，公式法分解因式，提取公因式后利用平方差公式进行二次分解，注意分解要彻底．3．①②③④【分析】根据作图方法，逐个推理证明即可．【详解】解：①如图1，由作图可知，BC的垂直平分线经过圆心O，因为OD⊥BC，所以，点D是弧的中点；②如图2，连接BC，∵是⊙O的直径，∴∠ACB=90°，∵OD∥AC，∴OD⊥BC，所以，点D是弧的中点；③如图3，∵∠BAD=∠CAD，所以，点D是弧的中点；④如图4，连接AD，∵是⊙O的直径，∴∠ADB=90°，∵AE=AB，∴∠BAD=∠CAD，所以，点D是弧的中点；故答案为：①②③④．【点睛】本题考查了垂径定理和圆周角的性质，解题关键是熟练运用相关性质进行证明推理．4．0．【分析】利用根的判别式列出方程，再确定c的最小值即可．【详解】解：∵关于x的一元二次方程有两个相等的实数根，∴，∴，则c的最小值是0，故答案为：0．【点睛】本题考查了一元二次方程根的判别式，解题关键是熟练运用一元二次方程根的判别式列出方程，根据非负数的性质确定最值．5．①②③【分析】根据题目表格所给的9种出行方式的相应数据对选项进行逐一判断即可得到答案．【详解】解：①要使出行费用尽可能少，由表格数据可知，出行方式2、3、4的费用均为3元比其他6种出行方式费用都少，故此说法正确；②出行方式1，出行时间47分钟，花费4元，对比较其他出行方式，出行时间最少，花费也较少，故此说法正确；③由题意可知方式5、6、7、8为公交车和地铁混合出行方式，故平均出行时间=出行总时间÷4，即平均出行时间=（60+56+55+57）÷4=57，故此说法正确；④题目未给出骑共享单车的时间和收费模式，无法计算，故此说法错误．故答案为：①②③．【点睛】本题主要考查了出行方式费用和时间的相关知识点，解题的关键在于能够读懂题意进行解答．6．     1（答案不唯一）     -2（答案不唯一）【分析】举出一个反例：a=1，b=-2，说明命题“若a＞b，则a2＞b2”是错误的即可．【详解】解：当a=1，b=-2时，满足a＞b，但是a2=1，b2=4，a2＜b2，∴命题“若a＞b，则a2＞b2”是错误的．故答案为：1、-2．（答案不唯一）【点睛】此题主要考查了命题与定理，要熟练掌握，解答此题的关键是要明确：任何一个命题非真即假．要说明一个命题的正确性，一般需要推理、论证，而判断一个命题是假命题，只需举出一个反例即可．7．乙【分析】根据方差的意义判断．方差反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．【详解】解：∵，，∴，∴甲、乙两人中成绩稳定的是乙；故答案为：乙．【点睛】本题考查了方差的意义：反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．8．【分析】设买美酒x斗，买普通酒y斗，根据“美酒一斗的价格是50钱、买两种酒2斗共付30钱”列出方程组．【详解】设买美酒x斗，买普通酒y斗，依题意得：，故答案是：．【点睛】考查了由实际问题抽象出二元一次方程组，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系，列方程组．9．【分析】首先根据题意画出树状图，然后由树状图求得所有等可能的结果与a+b＞4的情况，再利用概率公式即可求得答案．【详解】画树状图得：∵共有12种等可能的结果，任取两个不同的数，a+b＞4的有8种结果，∴a+b＞4的概率是＝，故答案为：．【点睛】本题考查了列表法与树状图法：运用列表法或树状图法展示所有可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率．10．③④【分析】根据函数图象所给的信息，逐一判断．【详解】由函数图象可知，甲走完全程需要82.3秒，乙走完全程需要90.2秒，甲队率先到达终点，故①错误；由函数图象可知，甲、乙两队都走了300米，路程相同，故②错误；由函数图象可知，在47.8秒时，两队所走路程相等，均为174米，故③正确；由函数图象可知，从出发到13.7秒的时间段内，甲队的速度慢，故④正确．∴正确判断的有：③④．故答案为：③④．【点睛】本题考查了函数图象的读图能力．要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件，结合实际意义得到正确的结论．11．﹣5【分析】先根据整式的混合运算法则化简原式，再将x2+x＝3代入计算可得．【详解】2（x﹣2）（x+2）﹣x（x﹣1）＝2（x2﹣4）﹣x2+x＝2x2﹣8﹣x2+x＝x2+x﹣8，∵x2+x﹣3＝0，∴x2+x＝3，则原式＝3﹣8＝﹣5，故答案为：﹣5．【点睛】本题主要考查代数式求值，解题的关键是掌握整式的混合运算顺序和运算法则及整体代入思想的运用．12．5【分析】找出ai+bi的值，结合对于任意的Mi＝{ai，bi}和Mj＝{aj，bj）（i≠j，1≤i≤s，1≤j≤s）都有ai+bi≠aj+bj，即可得出s的最大值．【详解】∵﹣1+1＝0，﹣1+2＝1，﹣1+3＝2，0+2＝2，0+3＝3，2+3＝5，∴ai+bi共有5个不同的值．又∵对于任意的Mi＝{ai，bi}和Mj＝{aj，bj）（i≠j，1≤i≤s，1≤j≤s）都有ai+bi≠aj+bj，∴s的最大值是5．故答案为：5．【点睛】本题是一道考查数字的变化类的题型，找出ai+bi共有几个不同的值是解题的关键．13．11．【分析】根据垂直平分线的性质：垂直平分线上的点到线段两端点的距离相等，即可得到AE=BE，则，代入即可求解．【详解】解：∵AB的垂直平分线交A于点D，交BC于点E，∴AE=BE，∵，∴，∵，，∴．故答案为：11．【点睛】本题主要考查的是垂直平分线的性质，垂直平分线上的点到线段两端点的距离相等，掌握垂直平分线的性质是解题的关键．