高中数学高考命题卷（07） 决胜2021新高考数学命题卷（新高考地区专用）（原卷版）

这是一份高中数学高考命题卷（07） 决胜2021新高考数学命题卷（新高考地区专用）（原卷版），共7页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
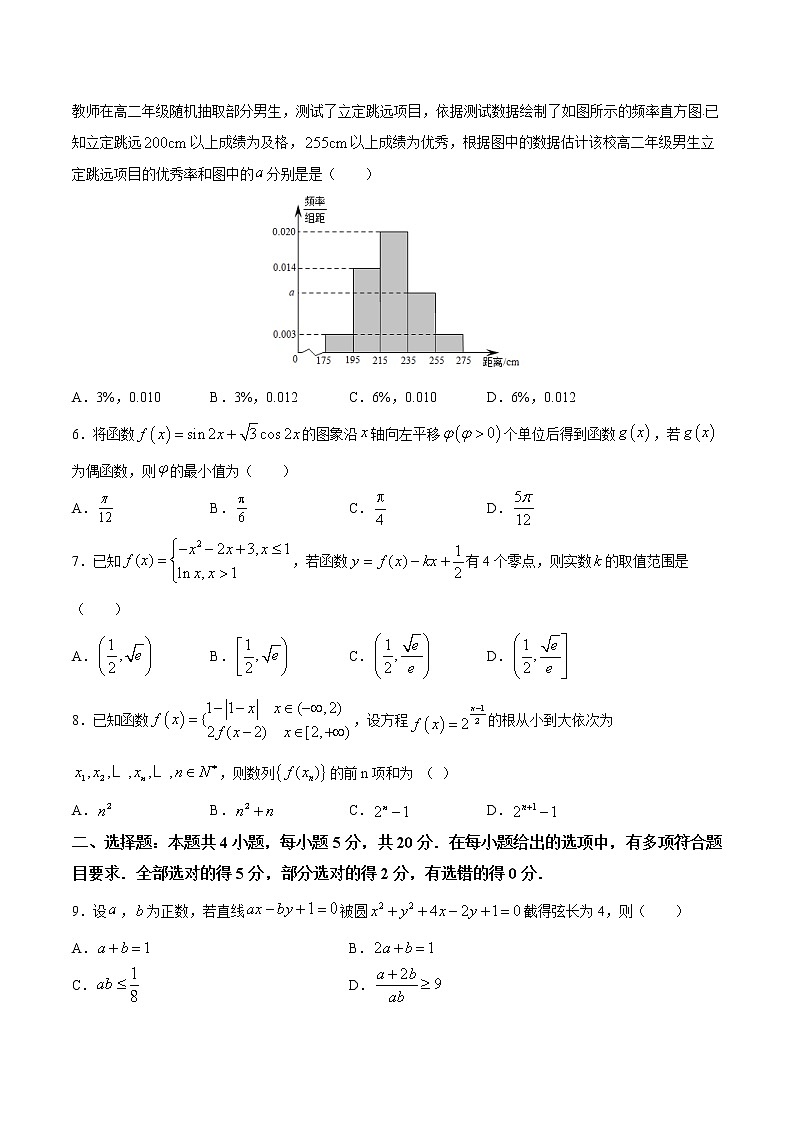
决胜2021新高考数学测试数学 命题卷（07）一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知复数，则复数在复平面内对应的点位于（    ）A．第一县象限 B．第二象限C．第三象限 D．第四象限2．已知全集为，集合，，则（    ）A． B．C．或 D．或3．已知命题空间两平面，直线，则直线；命题若关于的方程有两个不同实根，，则．下列命题为真命题的是（    ）A． B． C． D．4．在新冠肺炎疫情期间，某学校定期对教室进行药熏消毒.教室内每立方米空气中的含药量（单位：毫克）随时间（单位：小时）的变化情况如图所示.在药物释放的过程中，与成正比；药物释放完毕后，与的函数关系式为（为常数）.据测定，当空气中每立方米的含药量降低到0.2毫克以下时，学生方可进入教室.那么，从药物释放开始到学生能回到教室，至少在（    ）（参考数值）A．42分钟后 B．48分钟后C．50分钟后 D．60分钟后5．为落实《国家学生体质健康标准》达标测试工作，全面提升学生的体质健康水平，某校高二年级体育组教师在高二年级随机抽取部分男生，测试了立定跳远项目，依据测试数据绘制了如图所示的频率直方图.已知立定跳远以上成绩为及格，以上成绩为优秀，根据图中的数据估计该校高二年级男生立定跳远项目的优秀率和图中的分别是是（    ）A．3%，0.010 B．3%，0.012 C．6%，0.010 D．6%，0.0126．将函数的图象沿轴向左平移个单位后得到函数，若为偶函数，则的最小值为（    ）A． B． C． D．7．已知，若函数有4个零点，则实数的取值范围是（    ）A． B． C． D．8．已知函数，设方程的根从小到大依次为，则数列的前n项和为 （ ）A． B． C． D．二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9．设，为正数，若直线被圆截得弦长为4，则（    ）A． B．C． D．10．已知抛物线，为的焦点，过焦点且倾斜角为的直线交抛物线于，两点，则下列说法正确的是（    ）A．在点处的切线方程为B．C．过抛物线准线上的任意一点作的切线，则过两切点，的弦必过焦点D．11．已知函数，则下列说法正确的是（    ）A．有且只有一个极值点B．设，则与的单调性相同C．有且只有两个零点D．在上单调递增12．如图所示，在棱长为的正方体中，过对角线的一个平面交棱于点，交棱于点，得四边形，在以下结论中，正确的是（    ）A．四边形有可能是梯形B．四边形在底面内的投影一定是正方形C．四边形有可能垂直于平面D．四边形面积的最小值为三、填空题：本题共4小题，每小题5分，共20分．13．已知在等腰直角中，，若，则等于________.14．新型冠状病毒蔓延以来，世界各国都在研制疫苗，某专家认为，某种抗病毒药品对新型冠状病毒具有抗病毒、抗炎作用，假如规定每天早上7：00和晚上7：00各服药一次，每次服用该药药量700毫克具有抗病毒功效，若人的肾脏每12小时从体内滤出这种药的70%，该药在人体内含量超过1000毫克，就将产生副作用，若人长期服用这种药，则这种药__________（填“会”或者“不会”）对人体产生副作用.15．已知双曲线：与抛物线：的焦点重合，过点作直线与抛物线交于、两点（点在轴上方）且满足，若直线只与双曲线右支相交于两点，则双曲线的离心率的取值范围是______．16．定义在上的函数满足：，函数，若，则______．四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．在①，②，③，这三个条件中任选一个，补充在下面的问题中，并解决该问题.已知的内角，，的对边分别为，，，___________，，，求的面积.      18．已知数列对任意的都满足.（1）求数列的通项公式；（2）令，求数列的前项和为.          19．在一次大范围的随机知识问卷调查中，通过随机抽样，得到参加问卷调查的100人的得分统计结果如下表所示：得分频数213212524114（1）由频数分布表可以大致认为，此次问卷调查的得分，近似为这100人得分的平均值(同一组中的数据用该组区间的左端点值作代表).①求的值；②若，求的值；（2）在（1）的条件下，为此次参加问卷调查的市民制定如下奖励方案：①得分不低于的可以获赠2次随机话费，得分低于的可以获赠1次随机话费；②每次获赠的随机话费和对应的概率为：赠送话费的金额(单位：元)2050概率现有市民甲参加此次问卷调查，记(单位：元)为该市民参加问卷调查获赠的话费，求的分布列与数学期望.        20．如图，四边形为正方形，，，为锐角三角形，，分别是边，的中点，直线与平面所成的角为.（1）求证：平面；（2）若为锐角三角形，求二面角的余弦值.   21．已知椭圆的长轴长是焦距的倍，且过点.（1）求椭圆C的标准方程；（2）点P是圆心在原点O，半径为的圆O上的一个动点，过点P作椭圆的两条切线，且分别交其圆O于点E､F，求动弦长的取值范围.        22．设函数，，．（1）讨论的单调性；（2）当且时，函数，证明：存在极小值点，且．