高中数学高考全国通用版2019版高考数学一轮复习第九单元不等式学案文

这是一份高中数学高考全国通用版2019版高考数学一轮复习第九单元不等式学案文，共48页。
第九单元 不等式
教材复习课“不等式”相关基础知识一课过

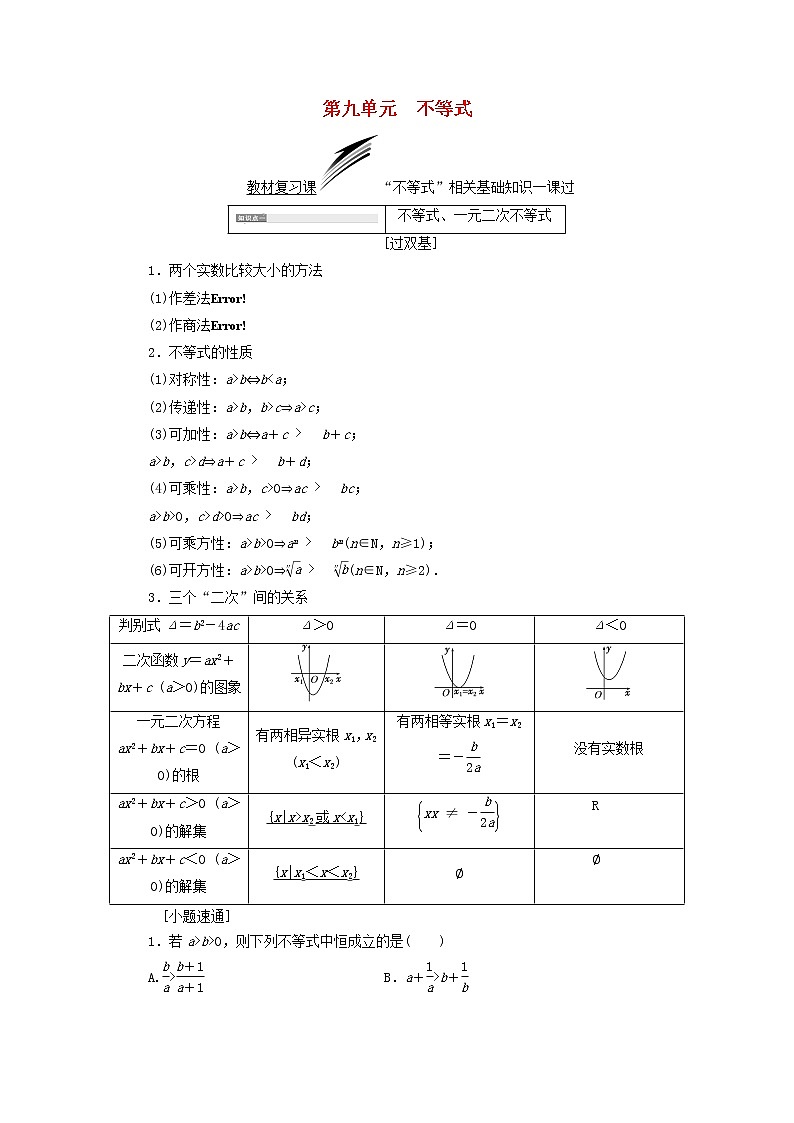
不等式、一元二次不等式
[过双基]
1．两个实数比较大小的方法
(1)作差法
(2)作商法
2．不等式的性质
(1)对称性：a>b⇔bb，b>c⇒a>c；
(3)可加性：a>b⇔a＋cb＋c；
a>b，c>d⇒a＋cb＋d；
(4)可乘性：a>b，c>0⇒acbc；
a>b>0，c>d>0⇒acbd；
(5)可乘方性：a>b>0⇒anbn(n∈N，n≥1)；
(6)可开方性：a>b>0⇒(n∈N，n≥2)．
3．三个“二次”间的关系
判别式Δ＝b2－4ac
Δ＞0
Δ＝0
Δ＜0
二次函数y＝ax2＋bx＋c (a＞0)的图象



一元二次方程
ax2＋bx＋c＝0 (a＞0)的根
有两相异实根x1，x2 (x1＜x2)
有两相等实根x1＝x2＝－
没有实数根
ax2＋bx＋c＞0 (a＞0)的解集
{x|x>x2或xb>0，则下列不等式中恒成立的是(　　)
A.>　　　　　　 B．a＋>b＋
C．a＋>b＋ D.>
解析：选C　由a>b>0⇒0N B．M ≥N
C．M＜N D．M≤N
解析：选A　由题意知，M－N＝2a(a－2)－(a＋1)(a－3)＝2a2－4a－(a2－2a－3)＝(a－1)2＋2>0恒成立，所以M>N.
3．已知一元二次不等式f(x)＞0的解集为xx＜－1或x＞，则f(10x)＞0的解集为(　　)
A．{x|x＜－1或x＞lg 2} B．{x|－1＜x＜lg 2}
C．{x|x＞－lg 2} D．{x|x＜－lg 2}
解析：选C　一元二次不等式f(x)＞0的解集为xx＜－1或x＞，则不等式f(10x)＞0可化为10x＜－1或10x＞，解得x＞lg ，即x＞－lg 2，所以所求不等式的解集为{x|x＞－lg 2}．
4．不等式－6x2＋2＜x的解集是________．
解析：不等式－6x2＋2＜x可化为6x2＋x－2＞0，
即(3x＋2)(2x－1)＞0，
解不等式得x，
所以该不等式的解集是∪.
答案：∪
[清易错]
1．在乘法法则中，要特别注意“乘数c的符号”，例如当c≠0时，有a>b⇒ac2>bc2；若无c≠0这个条件，a>b⇒ac2>bc2就是错误结论(当c＝0时，取“＝”)．
2．对于不等式ax2＋bx＋c>0，求解时不要忘记讨论a＝0时的情形．
3．当Δ0(a≠0)的解集为R还是∅，要注意区别a的符号．
1．若(m＋1)x2－(m－1)x＋3(m－1)0，b>0.
(2)等号成立的条件：当且仅当a＝b.
2．几个重要的不等式
(1)a2＋b2≥ 2ab(a，b∈R)；
(2)＋≥(a，b同号)；
(3)ab≤2(a，b∈R)；
(4)2≤(a，b∈R)．
3．算术平均数与几何平均数
设a＞0，b>0，则a，b的算术平均数为，几何平均数为，基本不等式可叙述为：两个正数的算术平均数不小于它们的几何平均数．
4．利用基本不等式求最值问题
已知x>0，y>0，则
(1)如果xy是定值p，那么当且仅当x＝y时，x＋y有最小值是2(简记：积定和最小)．
(2)如果x＋y是定值q，那么当且仅当x＝y时，xy有最大值是(简记：和定积最大)．
　
1．若实数a，b满足＋＝，则ab的最小值为(　　)
A. B．2
C．2 D．4
解析：选C　由＋＝，知a＞0，b＞0，
所以＝＋≥2 ，即ab≥2，
当且仅当即a＝，b＝2时取“＝”，
所以ab的最小值为2.
2．已知直线2ax＋by－2＝0(a＞0，b＞0)过点(1,2)，则＋的最小值是(　　)
A．2 B．3
C．4 D．1
解析：选C　由直线2ax＋by－2＝0(a＞0，b＞0)过点(1,2)，
可得2a＋2b＝2，即a＋b＝1.
则＋＝(a＋b)＝2＋＋≥2＋2 ＝4，当且仅当a＝b＝时取等号．
∴＋的最小值为4.
3．已知x，y∈R且2x＋2y＝1，则x＋y的取值范围为________．
解析：根据题意知，2x＞0,2y＞0，
所以1＝2x＋2y≥2＝2，
即2x＋y≤＝2－2，x＋y≤－2，
所以x＋y的取值范围为(－∞，－2]．
答案：(－∞，－2]
[清易错]
1．求最值时要注意三点：一是各项为正；二是寻求定值；三是考虑等号成立的条件．
2．多次使用基本不等式时，易忽视取等号的条件的一致性．
1．在下列函数中，最小值等于2的函数是(　　)
A．y＝x＋
B．y＝cos x＋
C．y＝
D．y＝ex＋－2
解析：选D　当x0，所以≥＝＝4ab＋≥2＝4，当且仅当时取等号，故的最小值是4.
答案：4

一、选择题
1．(2018·洛阳统考)已知aab>a
C．ab>a>ab2 D．ab>ab2>a
解析：选D　∵－10，则2lg≥lg a＋lg b
D．若x∈R，则x2＋>1
解析：选C　∵a2－6a＋9＝(a－3)2≥0，∴A错误；显然B不正确；∵a>0，b>0，∴≥.∴2lg≥2lg＝lg(ab)＝lg a＋lg b，∴C正确；∵当x＝0时，x2＋＝1，∴D错误，故选C.
3．若角α，β满足－