高中数学高考全国通用版2019版高考数学一轮复习鸭部分不等式选讲学案文

这是一份高中数学高考全国通用版2019版高考数学一轮复习鸭部分不等式选讲学案文，共36页。
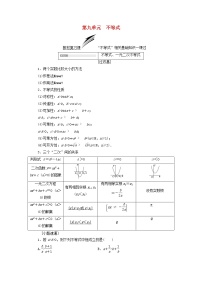
不等式选讲
第1课绝对值不等式
[过双基]
1．绝对值三角不等式
定理1：如果a，b是实数，则|a＋b|≤|a|＋|b|，当且仅当ab≥0时，等号成立．
定理2：如果a，b，c是实数，那么|a－c|≤|a－b|＋|b－c|，当且仅当(a－b)(b－c)≥0时，等号成立．
2．绝对值不等式的解法
(1)含绝对值的不等式|x|a的解集
不等式
a>0
a＝0
a0)型不等式的解法：
①|ax＋b|≤c⇔－c≤ax＋b≤c；
②|ax＋b|≥c⇔ax＋b≥c或ax＋b≤－c.
(3)|x－a|＋|x－b|≥c，|x－a|＋|x－b|≤c(c>0)型不等式的解法：
①利用绝对值不等式的几何意义求解；
②利用零点分段法求解；
③构造函数，利用函数的图象求解．
　
1．不等式|x＋1|－|x－2|≥1的解集是________．
解析：f(x)＝|x＋1|－|x－2|＝
当－1a或|f(x)|0，此时解集为∅；
当－1≤x≤1时，x＋1＋(x－1)＋1>0，
即x>－，此时－1时，x＋1－(x－1)＋1>0，
即3>0，此时x>1.
综上所述，不等式f(x)>0的解集为.
(2)依题意，方程f(x)＝x等价于a＝|x－1|－|x＋1|＋x，
令g(x)＝|x－1|－|x＋1|＋x.
∴g(x)＝.
画出函数g(x)的图象如图所示，

∴要使原方程只有一个实数根，只需a>1或a时，原不等式转化为4x≤6⇒0时，要证明a>b，只要证明>1即可，这种方法称为求商比较法．
(3)用比较法证明不等式的一般步骤是：作差(商)—变形—判断—结论，而变形的方法一般有配方、通分和因式分解．　　
[即时演练]
求证：当x∈R时，1＋2x4≥2x3＋x2.
证明：法一：(1＋2x4)－(2x3＋x2)
＝2x3(x－1)－(x＋1)(x－1)
＝(x－1)(2x3－x－1)
＝(x－1)(2x3－2x＋x－1)
＝(x－1)[2x(x2－1)＋(x－1)]
＝(x－1)2(2x2＋2x＋1)
＝(x－1)2≥0，
所以1＋2x4≥2x3＋x2.
法二：(1＋2x4)－(2x3＋x2)
＝x4－2x3＋x2＋x4－2x2＋1
＝(x－1)2·x2＋(x2－1)2≥0，
所以1＋2x4≥2x3＋x2.

综合法证明不等式
[典例]　已知a，b均为正数，且a＋b＝1，求证：
(1)(ax＋by)2≤ax2＋by2；
(2)2＋2≥.
[证明]　(1)(ax＋by)2－(ax2＋by2)＝a(a－1)x2＋b(b－1)y2＋2abxy，
因为a＋b＝1，
所以a－1＝－b，b－1＝－a，又a，b均为正数，
所以a(a－1)x2＋b(b－1)y2＋2abxy
＝－ab(x2＋y2－2xy)
＝－ab(x－y)2≤0，当且仅当x＝y时等号成立．
所以(ax＋by)2≤ax2＋by2.
(2)2＋2＝4＋a2＋b2＋
＝4＋a2＋b2＋＋＝4＋a2＋b2＋1＋＋＋＋＋1＝4＋(a2＋b2)＋2＋＋≥6＋＋4＋2＝，
当且仅当a＝b＝时，等号成立，
所以2＋2≥.
[方法技巧]
1．综合法证明不等式的方法
综合法证明不等式，要着力分析已知与求证之间，不等式的左右两端之间的差异与联系．合理进行转换，恰当选择已知不等式，这是证明的关键．
2．综合法证明时常用的不等式
(1)a2≥0.
(2)|a|≥0.
(3)a2＋b2≥2ab，它的变形形式有：
a2＋b2≥2|ab|；a2＋b2≥－2ab；(a＋b)2≥4ab；
a2＋b2≥(a＋b)2；≥2.
(4)≥，它的变形形式有：
a＋≥2(a>0)；＋≥2(ab>0)；
＋≤－2(ab0，b>0,2c>a＋b，求证：c－