2023年中考总复习11：一元二次方程、分式方程的解法及应用--知识讲解（基础）

中考总复习：一元二次方程、分式方程的解法及应用—知识讲解（基础）

责编：常春芳

【考纲要求】

1.理解配方法，会用因式分解法、公式法、配方法解简单的数字系数的一元二次方程；

2. 会解分式方程，解分式方程的基本思想是把分式方程转化成整式方程，把未知问题转化成已知问题，从而渗透数学的转化思想．

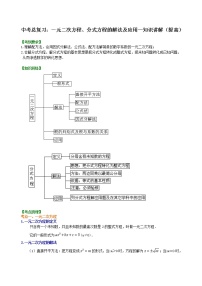
【知识网络】

【考点梳理】

考点一、一元二次方程

1.一元二次方程的定义

只含有一个未知数，并且未知数的最高次数是2的整式方程，叫做一元二次方程．

它的一般形式为(a≠0)．

2.一元二次方程的解法

    （1）直接开平方法：把方程变成的形式，当m＞0时，方程的解为；当m＝0时，方程的解；当m＜0时，方程没有实数解．

    （2）配方法：通过配方把一元二次方程变形为的形式，再利用直接开平方法求得方程的解．

（3）公式法：对于一元二次方程，当时，它的解为．

    （4）因式分解法：把方程变形为一边是零，而另一边是两个一次因式积的形式，使每一个因式等于零，就得到两个一元一次方程，分别解这两个方程，就得到原方程的解．

要点诠释：

直接开平方法和因式分解法是解一元二次方程的特殊方法，配方法和公式法是解一元二次方程的一般方法．

3．一元二次方程根的判别式

一元二次方程根的判别式为．

△>0方程有两个不相等的实数根；

△＝0方程有两个相等的实数根；

△<0方程没有实数根．

上述由左边可推出右边，反过来也可由右边推出左边．

要点诠释：

    △≥0方程有实数根.

4．一元二次方程根与系数的关系

如果一元二次方程(a≠0)的两个根是，那么．

考点二、分式方程

 1.分式方程的定义

分母中含有未知数的有理方程，叫做分式方程．

要点诠释：

（1）分式方程的三个重要特征：①是方程；②含有分母；③分母里含有未知量.
　　（2）分式方程与整式方程的区别就在于分母中是否含有未知数(不是一般的字母系数)，分母中含有未知数的方程是分式方程，不含有未知数的方程是整式方程，如：关于的方程和都是分式方程，而关于的方程和都是整式方程.

 2.分式方程的解法

去分母法，换元法．

3.解分式方程的一般步骤
　　　(1)去分母，即在方程的两边都乘以最简公分母，把原方程化为整式方程；
　　　(2)解这个整式方程；
　　　(3)验根：把整式方程的根代入最简公分母，使最简公分母不等于零的根是原方程的根，使最简公
　　　 　分母等于零的根是原方程的增根.

口诀：“一化二解三检验”.

要点诠释：

解分式方程时，有可能产生增根，增根一定适合分式方程转化后的整式方程，但增根不适合原方程，可使原方程的分母为零，因此必须验根．

考点三、一元二次方程、分式方程的应用

1．应用问题中常用的数量关系及题型

    (1)数字问题(包括日历中的数字规律)

    关键会表示一个两位数或三位数，对于日历中的数字问题关键是弄清日历中的数字规律．

    (2)体积变化问题

    关键是寻找其中的不变量作为等量关系.

    (3)打折销售问题

    其中的几个关系式：利润＝售价-成本价(进价)，利润率＝×100%．

    明确这几个关系式是解决这类问题的关键．

    (4)关于两个或多个未知量的问题

    重点是寻找到多个等量关系，能够设出未知数，并且能够根据所设的未知数列出方程.

    (5)行程问题

    对于相遇问题和追及问题是列方程解应用题的重点问题，也是易出错的问题，一定要分析其中的特点，同向而行一般是追及问题，相向而行一般是相遇问题．

    注意：追及和相遇的综合题目，要分析出哪一部分是追及，哪一部分是相遇.

    (6)和、差、倍、分问题

    增长量＝原有量×增长率；

    现有量＝原有量+增长量；

    现有量＝原有量-降低量．

2．解应用题的步骤

(1)分析题意，找到题中未知数和题给条件的相等关系；

(2)设未知数，并用所设的未知数的代数式表示其余的未知数；

(3)找出相等关系，并用它列出方程；

(4)解方程求出题中未知数的值；

(5)检验所求的答数是否符合题意，并做答．

要点诠释：

 方程的思想，转化(化归)思想，整体代入，消元思想，分解降次思想，配方思想，数形结合的思想用数学表达式表示与数量有关的语句的数学思想．

      注意：①设列必须统一，即设的未知量要与方程中出现的未知量相同；②未知数设出后不要漏棹单位；③列方程时，两边单位要统一；④求出解后要双检，既检验是否适合方程，还要检验是否符合题意．

【典型例题】

类型一、一元二次方程 

1．用配方法解一元二次方程：

【思路点拨】

把二次项系数化为1，常数项右移，方程两边都加上一次项系数一半的平方，再用直接开平方法解出未知数的值.

【答案与解析】

移项，得

二次项系数化为1，得

配方

由此可得

，

【总结升华】用配方法解一元二次方程的一般步骤：
　　　①把原方程化为的形式；
　　　②将常数项移到方程的右边；方程两边同时除以二次项的系数，将二次项系数化为1；
　　　③方程两边同时加上一次项系数一半的平方；
　　　④再把方程左边配成一个完全平方式，右边化为一个常数；
　　　⑤若方程右边是非负数，则两边直接开平方，求出方程的解；若右边是一个负数，则判定此方程

无实数解.
 

举一反三：

【变式】用配方法解方程x2-7x-1=0．
【答案】

将方程变形为x2-7x=1，两边加一次项系数的一半的平方，得
　　　　x2-7x+=1+，所以有=1+．
　　　　直接开平方，得x-=或x-=-．
　　　　所以原方程的根为 x=或x=．
 

2．（2015•咸宁）已知关于x的一元二次方程mx2﹣（m+2）x+2=0．

（1）证明：不论m为何值时，方程总有实数根；

（2）m为何整数时，方程有两个不相等的正整数根．

【思路点拨】判别式大于0，二次项系数不等于0.

【答案与解析】

（1）证明：△=（m+2）2﹣8m

=m2﹣4m+4

=（m﹣2）2，

∵不论m为何值时，（m﹣2）2≥0，

∴△≥0，

∴方程总有实数根；

（2）解：解方程得，x=，

x1=，x2=1，

∵方程有两个不相等的正整数根，

∴m=1或2，

∵m=2不合题意，

∴m=1．

【总结升华】

（1）注意隐含条件m≠0；（2）注意整数根的限制条件的应用，求出m的值，要验证m的值是否符合题意.

举一反三：

【变式】已知关于x的方程．

（1）求证方程有两个不相等的实数根．

（2）当m为何值时，方程的两根互为相反数？并求出此时方程的解．

【答案】

（1）证明:因为△=  

                  = 

       所以无论取何值时， △>0，所以方程有两个不相等的实数根．

（2）解：因为方程的两根互为相反数，所以， 

根据方程的根与系数的关系得，解得， 

所以原方程可化为，解得，.

类型二、分式方程

3．（2015•贺州）解分式方程：=﹣．

【思路点拨】先去分母将分式方程化为整式方程，求出整式方程的解，再进行检验.

【答案与解析】

解：方程两边同乘以（2x+1）（2x﹣1），得

x+1=3(2x-1)-2(2x+1)

x+1=2x-5，

解得x=6．

检验：x=6是原方程的根．

故原方程的解为：x=6．

【总结升华】首先要确定各分式分母的最简公分母，在方程两边乘这个公分母时不要漏乘，解完后记着要验根.

举一反三：

【变式1】解分式方程：．

【答案】方程两边同乘以，得

     ． 

   　．

               ． 

　　　   经检验：是原方程的解，

所以原方程的解是． 

【高清课程名称：一元二次方程、分式方程的解法及应用    高清ID号： 405754

关联的位置名称（播放点名称）：例1（1）】

【变式2】方程的解是x=      ．

【答案】.

4．若解分式方程产生增根，则m的值是（    ）

        A.    B.       C.   D.

【思路点拨】先把原方程化为整式方程，再把可能的增根分别代入整式方程即可求出m的值.

【答案】D；

【解析】由题意得增根是：

化简原方程为：把代入解得，

故选择D.

【总结升华】分式方程产生的增根，是使分母为零的未知数的值.

举一反三：

【高清课程名称：一元二次方程、分式方程的解法及应用   高清ID号：  405754

关联的位置名称（播放点名称）：例1（2）-例2】

【变式】若关于的方程无解，则的值是           ．

【答案】1.

类型三、一元二次方程、分式方程的应用

5．轮船在一次航行中顺流航行80千米，逆流航行42千米，共用了7小时；在另一次航行中，用相同的时间，顺流航行40千米，逆流航行70千米.求这艘轮船在静水中的速度和水流速度.

【思路点拨】

在航行问题中的等量关系是“顺流速度＝静水速度＋水流速度； 逆流速度＝静水速度－水流速度”，两次航行提供了两个等量关系.

【答案与解析】

设船在静水中的速度为x千米/小时，水流速度为y千米/小时

      由题意，得

      答：水流速度为3千米/小时，船在静水中的速度为17千米/小时.

【总结升华】

流水问题公式：顺流速度＝静水速度＋水流速度；  逆流速度＝静水速度－水流速度；

静水速度＝(顺流速度＋逆流速度)÷2；水流速度＝(顺流速度－逆流速度)÷2.

举一反三：

【变式】甲、乙两班同学参加“绿化祖国”活动，已知乙班每小时比甲班多种2棵树，甲班种60棵所用的时间与乙班种66棵树所用的时间相等，求甲、乙两班每小时各种多少棵树？

【答案】设甲班每小时种x棵树，则乙班每小时种（x+2）棵树，

        由题意得：

       答：甲班每小时种树20棵，乙班每小时种树22棵.

6．某服装厂生产一批西服，原来每件的成本价是500元，销售价为625元，经市场预测，该产品销售价第一个月将降低20%，第二个月比第一个月提高6%，为了使两个月后的销售利润达到原来水平，该产品的成本价平均每月应降低百分之几？

【思路点拨】

设该产品的成本价平均每月降低率为x，那么两个月后的销售价格为625（1-20%）（1+6%），两个月后的成本价为500（1-x）2，然后根据已知条件即可列出方程，解方程即可求出结果．

【答案与解析】

       设该产品的成本价平均每月应降低的百分数为x．

       625（1-20%）（1+6%）-500（1-x）2=625-500

       整理，得500（1-x）2=405，（1-x）2=0.81．

       1-x=±0.9，x=1±0.9，

       x1=1.9（舍去），x2=0.1=10%．

       答：该产品的成本价平均每月应降低10%．

【总结升华】

题目中该产品的成本价在不断变化，销售价也在不断变化，要求变化后的销售利润不变，即利润仍要达到125元，关键在于计算和表达变动后的销售价和成本价．