高中数学高考专题10 三角函数图象与性质(解析版)
展开专题10 三角函数图像与性质
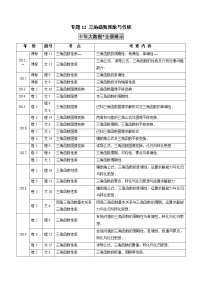
命题规律 | 内 容 | 典 型 |
1 | 已知函数的图象研究其性质 | 2020年高考全国Ⅰ卷文数7 |
2 | 可化为形如的函数性质的研究 | 2020年高考天津卷8 |
3 | 含有三角函数的函数图像识别 | 2019年高考全国Ⅰ卷文数 |
4 | 研究将已知函数图象进行的变换后所得函数的性质 | 020年高考江苏卷10 |
5 | 研究关于某个三角函数的函数的性质 | 2020年高考全国Ⅲ卷文数12 |
命题规律一 已知函数()的图象研究函数性质
【解决之道】接此类问题,先根据图象求出解析式,已知f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象求其解析式时,A比较容易看图得出,困难的是求待定系数ω和φ,常用如下两种方法:①由ω=即可求出ω;确定φ时,若能求出离原点最近的右侧图象上升(或下降)的“零点”横坐标x0,则令ωx0+φ=0(或ωx0+φ=π),即可求出φ.②代入点的坐标,利用一些已知点(最高点、最低点或“零点”)坐标代入解析式,再结合图形解出ω和φ,若对A,ω的符号或对φ的范围有要求,则可用诱导公式变换使其符合要求.再根据解析研究函数的性质.
【三年高考】
1.【2020年高考全国Ⅰ卷文数7】设函数在的图像大致如下图,则的最小正周期为 ( )
A. B. C. D.
【答案】C
【解析】由图可得:函数图像过点,将它代入函数可得:,
又是函数图像与轴负半轴的第一个交点,∴,解得:,∴函数的最小正周期为,故选C.
2.【2020年高考山东卷10】右图是函数的部分图像,则 ( )
A. B. C. D.
【答案】BC
【解析】由函数图像可知:,则,所以不选A,
当时,,解得:,
即函数的解析式为:,
而,故选:BC.
命题规律二可化为形如的函数性质的研究
【解决之道】此类问题,先利用降幂公式、两角和与差的公式及辅助角公式将已知函数的解析式化为形式,再利用研究函数性质方法进行研究.
【三年高考】
1.【2020年高考天津卷8】已知函数.给出下列结论:
①的最小正周期为;
②是的最大值;
③把函数的图象上所有点向左平移个单位长度,可得到函数的图象.
其中所有正确结论的序号是( )
A.① B.①③ C.②③ D.①②③
【答案】B
【解析】因为,所以周期,故①正确;
,故②不正确;
将函数的图象上所有点向左平移个单位长度,得到的图象,故③正确.故选B.
2.【2020年高考北京卷14】若函数的最大值为,则常数的一个取值为 .
【答案】
【解析】∵
,
则,,∴,∴
3.【2019年高考全国Ⅱ卷文数】若x1=,x2=是函数f(x)=(>0)两个相邻的极值点,则=( )
A.2 B.
C.1 D.
【答案】A
【解析】由题意知,的周期,解得.故选A.
4.【2019年高考北京卷文数】设函数f(x)=cosx+bsinx(b为常数),则“b=0”是“f(x)为偶函数”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
【答案】C
【解析】时,,为偶函数;
为偶函数时,对任意的恒成立,即,,得对任意的恒成立,从而.从而“”是“为偶函数”的充分必要条件,故选C.
5.【2019年高考浙江卷】设函数.
(1)已知函数是偶函数,求的值;
(2)求函数的值域.
【答案】(1)或;(2).
【解析】(1)因为是偶函数,所以,对任意实数x都有,
即,
故,
所以.
又,
因此或.
(2)
.
因此,函数的值域是.
6.【2018年高考全国Ⅲ卷文数】函数的最小正周期为( )
A. B.
C. D.
【答案】C
【解析】,故所求的最小正周期为,故选C.
7.【2018年高考全国Ⅰ卷文数】已知函数,则( )
A.的最小正周期为π,最大值为3
B. 的最小正周期为π,最大值为4
C. 的最小正周期为,最大值为3
D.的最小正周期为,最大值为4
【答案】B
【解析】根据题意有,所以函数的最小正周期为,且最大值为,故选B.
8.【2018年高考全国Ⅱ卷文数】若在是减函数,则的最大值是( )
A. B.
C. D.
【答案】C
【解析】.当x∈时,∈,所以结合题意可知,,即,故所求a的最大值是,故选C.
9.【2018年高考江苏卷】已知函数的图象关于直线对称,则的值是________.
【答案】
【解析】由题意可得,所以,
因为,所以
10.【2018年高考北京卷文数】已知函数.
(1)求的最小正周期;
(2)若在区间上的最大值为,求的最小值.
【答案】(1);(2).
【解析】(1),
所以的最小正周期为.
(2)由(1)知.
因为,
所以.
要使得在上的最大值为,即在上的最大值为1.
所以,即.
所以的最小值为.
命题规律三 含有三角函数的函数图像识别
【解决之道】函数图象的识辨可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势.(3)从函数的奇偶性,判断图象的对称性.(4)从函数的特征点,排除不合要求的图象.利用上述方法排除、筛选选项.
【三年高考】
1.【2020年高考浙江卷4】函数在区间的图像大致为 ( )
A. B. C. D.
【答案】A
【思路导引】首先确定函数的奇偶性,然后结合函数在处的函数值排除错误选项即可确定函数的图像.
【解析】,,
∴函数是奇函数,故排除C,D,当时,,∴排除B,故选A.
2.【2019年高考全国Ⅰ卷文数】函数在的图像大致为( )
A. B.
C. D.
【答案】D
【解析】由,得是奇函数,其图象关于原点对称,排除A.又,排除B,C,故选D.
3.【2018年高考浙江卷】函数y=sin2x的图象可能是( )
A. B.
C. D.
【答案】D
【解析】令,因为,所以为奇函数,排除选项A,B;
因为时,,所以排除选项C,
故选D.
命题规律四 研究将已知函数图象进行的变换后所得函数的性质
【解决之道】解决此类问题,先根据图象变换方法求出变换后的解析式,再利用研究性质的方法研究变换后的所得函数的性质.
【三年高考】
1..【2020年高考江苏卷10】将函数的图象向右平移个单位长度,则平移后的图象中与轴最近的对称轴的方程是 .
【答案】
【解析】∵,将函数的图象向右平移个单位长度得,则的对称轴为,,即,,时,,时,,∴平移后的图象中与轴最近的对称轴的方程是.
2.【2019年高考天津卷文数】已知函数是奇函数,且的最小正周期为π,将的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为.若,则( )
A.−2 B.
C. D.2
【答案】C
【解析】∵为奇函数,∴,∵的最小正周期为π,∴,∴又,∴,∴,,故选C.
3.【2018年高考天津卷文数】将函数的图象向右平移个单位长度,所得图象对应的函数( )
A.在区间上单调递增 B.在区间上单调递减
C.在区间上单调递增 D.在区间上单调递减
【答案】A
【解析】由函数图象平移变换的性质可知:将函数的图象向右平移个单位长度之后的解析式为,则函数的单调递增区间满足,即,令可得函数的一个单调递增区间为,选项A正确,B错误;函数的单调递减区间满足:,即,令可得函数的一个单调递减区间为,选项C,D错误.
故选A.
命题规律五 研究关于某个三角函数的函数的性质
【解决之道】若含绝对值,可通过取绝对值,利用公司化为一个角的三角函数结合图象进行研究;若是关于某个三角函数的函数问题,结合所涉及三角函数的图象与性质、换元法等方法进行研究.
【三年高考】
1.【2020年高考全国Ⅲ卷文数12】已知函数,则 ( )
A.的最小值为 B.的图像关于轴对称
C.的图像关于直线对称 D.的图像关于直线对称
【答案】D
【解析】可以为负,所以A错;关于原点对称;
故B错;关于直线对称,故C错,D对,故选:D.
高中数学高考专题12 三角函数图象与性质(解析版): 这是一份高中数学高考专题12 三角函数图象与性质(解析版),共24页。试卷主要包含了若,是函数两个相邻的极值点,则,若在,是减函数,则的最大值是,函数的最小正周期为等内容,欢迎下载使用。
高中数学高考专题10 三角函数图象与性质(原卷版): 这是一份高中数学高考专题10 三角函数图象与性质(原卷版),共5页。试卷主要包含了已知函数的图象研究函数性质等内容,欢迎下载使用。
高中数学高考专题05 函数图象(解析版): 这是一份高中数学高考专题05 函数图象(解析版),共9页。试卷主要包含了函数f=在的图像大致为,函数在的图像大致为,函数的图像大致为,函数的部分图像大致为,已知函数=,则=的图像大致为,函数=在的图像大致为等内容,欢迎下载使用。