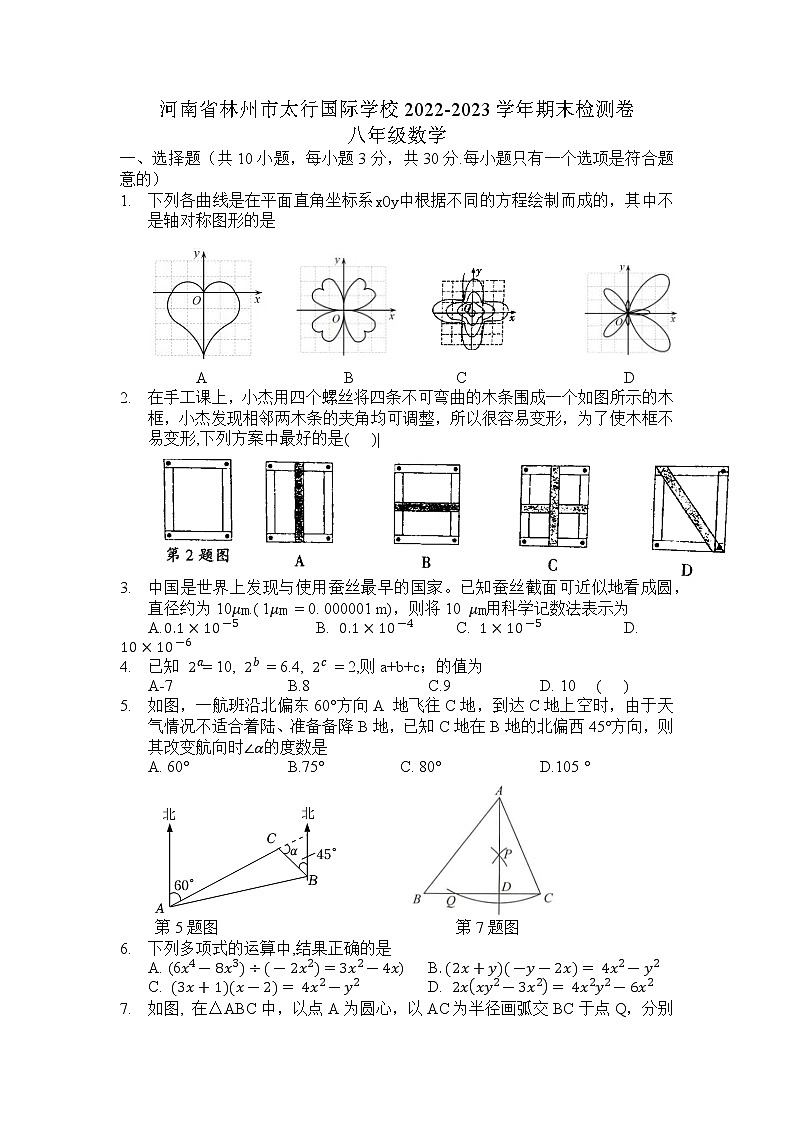
河南省林州市太行国际学校2022—2023学年上学期八年级期末数学检测试卷

这是一份河南省林州市太行国际学校2022—2023学年上学期八年级期末数学检测试卷，共6页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题（共10小题，每小题3分，共30分.每小题只有一个选项是符合题意的）
1.下列各曲线是在平面直角坐标系xOy中根据不同的方程绘制而成的，其中不是轴对称图形的是
A BCD
2.在手工课上，小杰用四个螺丝将四条不可弯曲的木条围成一个如图所示的木框，小杰发现相邻两木条的夹角均可调整，所以很容易变形，为了使木框不易变形,下列方案中最好的是()|
3.中国是世界上发现与使用蚕丝最早的国家。已知蚕丝截面可近似地看成圆，直径约为10μm.( 1μm = 0. 000001 m)，则将10 μm用科学记数法表示为
A.0.1×10-5B. 0.1×10-4C. 1×10-5D. 10×10-6
4.已知 2a= 10, 2b = 6.4, 2c = 2,则a+b+c；的值为
A-7B.8C.9D. 10()
5.如图，一航班沿北偏东60°方向A 地飞往C地，到达C地上空时，由于天气情况不适合着陆、准备备降B地，已知C地在B地的北偏西45°方向，则其改变航向时∠α的度数是
A. 60°B.75°C. 80°D.105 °
第5题图 第7题图
6.下列多项式的运算中,结果正确的是
A. (6x4-8x3)÷(-2x2)=3x2-4x)B. 2x+y-y-2x= 4x2-y2
C. 3x+1x-2= 4x2-y2D. 2xxy2-3x2= 4x2y2-6x2
7.如图, 在△ABC中，以点A为圆心，以AC为半径画弧交BC于点Q，分别以点C，Q为圆心，以大于12CQ为半径画弧交于点P,连接AP并延长，交BC于点D若BQ=3，DQ=4, ∠B = 45°,则△ABC的面积为（）
A.38.5B. 41C. 43.5D. 45.5
8.(数学文化）我国古代著作《四元玉鉴》记载“买椽多少”问题:六贯二百一十钱，倩人去买几株椽。每株脚钱三文足，无钱准与一株椽”其大意为:现请人代买一批椽，这批椽的价钱为6210文，如果每株椽的运费是3文，那么少拿一株椽后，剩下的椽的运费恰好等于一株椽的价钱，试问：6210文能买多少株椽？设这批椽的数量为x株，则符合题意的方程是( )
A. 3(x-1)=6210xB. 6210x-1=3
C. 3x-1=6210xD. 6210x=3
9.如图,AD，CD分别平分△ABC的外角∠EAC,若∠ABC=50°，则∠ABC的度数为( )
A. 50°B. 60°C. 65°D. 70°
第9题图 第10题图
10.如图，在△ABC中，AB=AC，AD是BC边的中线，DE丄AB于点E,DF丄AC于点F下列结论.①DE=DF;②BE=CF;③∠BDE=∠CDF;④∠BDE =∠DAF.其中正确的是（)
A.①②③ B.①②④C.②③④D. ①②③④
二、填空题（丼5小题，每小题3分，共I5分）
11.已知长方形的面积为12mn3，其中它的长为n2则该长方形的宽为______.
12.已知等腰三角形的腰长为3,底边长为方程|x-6| =3的解，则该等腰三角形的周长为
13.当关于x-mx-3-3m3-x=4的方程的解为x = 2时，m的值为 .
14.如图，在Rt△ABC中, ∠A= 90°，D为AB边上—点，连接CD，并过点D作DE丄BC于点E,已知AD=DE=3，∠B =30°，则CD的长为 .
A
B
C
D
E
第14题图
第15题图
15.如图, △ABC是等腰三角形，AB=AC,D,E是BC上两点，∠ADE=∠AED，延长AE至点F ，使AF=AC,已知∠BAD =20°,则∠EFC的度数为 .
三、解答题（共8小题.共75分.解答应写出过程）
16. (8 分）（1)计算：1-5--12-1-(3. 14-1)0;
(2)因式分解：-3a3b2+12a2b2-12ab2.
17.（9分)解分式方程:1-3x-4=x-34-x
18.(9分)先化简，再求值：(xx2-9-13-x)÷2x+3x,其中x是一元一次不等式组2x-4+10≤0x-3>-92的整数解。
19.(9分)如图，点E，B在线段AD上，AE=BD，EF⊥AD于点E，CB⊥AD于B，连接AC，连接分别交BC，AC于M,G，AC=DF；
(1).由上述条件可得∠C= ∠F，下面是小难同学的思考过程，请你在横线上填写内容，在括号内填写依据.
思考过程
∵ FE⊥AD 于点 E，CB⊥AD于点B
∴△ABC 和△DEF 是直角三角形
∵AE=BD.
∴AE+___=BD+EB,即____=DE（依据：等量代换）
在Rt△ABC 和Rt△DEF中,AB=___AC=DF
∴Rt△ABC ≅Rt△DEF(依据： )
∠C=∠F,依据：
（2）若∠A=30°，判断△CGM的形状
20.（9分）洛邑古城，被誉为“中原渡口”,位于河南省洛阳市老城区，包含多个历史时期保护建筑，周末，小洛、小阳两位同学约好同时从自己家出发骑行到洛邑古城游玩,已知小阳家到洛邑古城的路程为12 km，小洛家到洛邑古城的路程比小阳家到洛邑古城的路程远3 km,小洛骑车的骑车的平均速度为3.5 km/h,结果小洛与小阳同时到达，求小阳从家骑车到洛邑古城的平均速度。
21.(10分)如图,在平面直角坐标系中，点A（-2,1）、点B（ 3.1),点C(-6,7).
⑴依次连接机AB，AC，BC图中作△ABC关于x轴对称的△A'B'C',并写出点A'，B'， C'的坐标；
(2)在图中作△ABD,使它与△ABC全等（作出一个即可）;
(3)求以B，C，A，A'，C', B'为顶点的多边形的面积.
22.( 10分）如图，P是等边三角形ABC内的一点，连接AP, BP, CP,∠APC = 90°，∠APB=α，以BP为边作等边三角形PBD连接CD
α
(1)求证：△ABP ≅△CBD;
(2)当α = 150°时，若BP=3,求CP的长；
(3)若CD=CP,求α的度数
22.解：(1)∵P是等边三角形ABC内的一点∴AB=BC
∵BP为边作等边三角形PBD∴BP=BD，∠ABC=∠PBD=60°
∠ABC-∠PBC=∠PBD-∠PBC∴∠ABP=∠CDB∴△ABP ≅△CBD
（2）∵△ABP ≅△CBD，α = 150°∴∠BDC=∠APB=150°，∠BDP=60°∴∠PDC=90°
∠DPC=360°-150°-60°-90°=60°，BP=3=PD，PC=6
（3）∠α=60°+∠DPC=60°+（360°-60°-90°-∠α=60°，解得∠α=85°
23. (11分)如图①，在平面直角坐标系中，点A,点B分别在x轴负半轴和y轴正半轴上，点C在第二象限，且∠ACB = 90°，AC=BC，点 B 的坐标为（0，m)，点 C的纵坐标为n,满足m2+n2-2m-8n+17=0
(1)求点A的坐标
(2)如图②，点D是AB的中点，点E，F分别是边AC，BC上的动点，且DEDF，有点E，F移动过中，四边形的面积是否为定值？请说明理由；
x
y
A
B
C
D
F
E
图2
x
y
A
B
图1
(3)在平面直角坐标系中，是否存在点P,使得△PAC是以点A为直角顶点的等腰直角三角形，请直接写出满足条件的点P的坐标.
图1
参考答案
选择题1-5CDCBB6-10DAACD
填空题
11.12mn
12.9
13. -3
14.6
15.80°
解答题
16.解：(1)原式=4-2-1=1(2)原式=-3ab2a2-4a+4=-3ab2(a-2)2
17.解：1+34-x=x-34-x 4-x+34-x=x-34-x 7-x=x-3 ,x=5
18.解：原式=(x(x+3)(x-3)+1x-3)÷2x+3x=x+x+3(x+3)(x-3)×x2x+3=xx2-9
解不等式组2x-4+10≤0，x≤-1, x-3>-92,x>-32∴x=-1∴原式=-1(-1)2-9=18
19. 解：(1)EB;AB;DE;( 指斜边和一条直角边对应相等的两个直角三角形全等); 全等三角形的对应边相等，对应角相等.(2)∵ ∠A=30°, CB⊥AD∴∠ACB=60°，∵Rt△ABC ≅Rt△DEF
∠A=∠D=30°，CB⊥AD∴∠BMD=∠GMC=60°∴△CGM是等边三角形。
20.解：设小阳家到洛邑古城的平均速度为???ℎ,根据题意12+3?+3.5=12?，解得?=14,经检验，?=14是原分式方程的解。
答：小阳家到洛邑古城的平均速度为14km/h
21.（1）（2）如图所示
A
B
C
C'
A'
B'
D
（3）AB=3-（-2）=5，A?′=1−−1=2
?多边形=2?∆???+?四边形???′?′=2×12×5×7−1+5×2=40
B
C
P
D
第22题图
A
α
22.解：(1)∵P是等边三角形ABC内的一点∴AB=BC
∵BP为边作等边三角形PBD∴BP=BD，∠ABC=∠PBD=60°
∠ABC-∠PBC=∠PBD-∠PBC∴∠ABP=∠CDB∴△ABP ≅△CBD
（2）∵△ABP ≅△CBD，α = 150°∴∠BDC=∠APB=150°，∠BDP=60°∴∠PDC=90°
∠DPC=360°-150°-60°-90°=60°，BP=3=PD，PC=6
（3）∠α=60°+∠DPC=60°+（360°-60°-90°-∠α=60°，解得∠α=85°
23.解：（1）m2+n2-2m-8n+17=0
x
y
A
B
C
M
N
图1
∴m-12+n-42=0
∴m=1, n=4∴点B（0，1）
过点A作x轴垂线AM，过点C作y轴垂线CN，延长NC，与AM交于M，则∠AMC=∠BNC=∠ACB=90°∴∠MAC+∠ACM=∠ACM+∠NCB=90° , ∠MAC=∠NCB
在△AMC和△CNB中
∠AMC=∠CNB∠MAC=∠NCBAC=BC，∴△AMC≅△CNB，AM=CN=ON=4，BN=CM=4-1=3
∴MN=OA=CN+MC=4+3=7
∴点A的坐标为（-7，0）
x
y
A
B
C
D
F
E
图2
(2) 四边形CEDF的面积是定值
理由如下：连接CD∵AC=BC，D为BC的中点，∠ACB = 90°
∴CD⊥AB，CD平分∠ACB∴∠DCE=∠BCD= 45°，∠ABC= 45°
∴∠DCE=∠DBF，CD=BD
∵∠EDF=∠CDB=90°,∴∠EDC =∠FDB
∠EDC =∠FDB∠DCE=∠DBFCD=BD ∴△DCE≅△DBF
∴S四边形CEDF=S∆CED+S∆DCF=S∆FDB+S∆DCF=S∆CDB=12S∆ABC
（3）P（-3，-3）或P（-11，3）
图3
如图3，过A作AC垂线，使AP1=AC，延长P1A，使AP2=AP1分别过P1，P2向x轴作垂线，垂足为G，K，∴△AP1G≅∆ACM≅∆AP1K，∴AG=AM=AK=4，P1G=CM=P2K=3，∴OG=7-4=3，P1-3,-3;∵KO=AK+AO=11∴P2-11,3
∴满足条件的点的坐标为（-3，-3）或（-11，3）