高中数学高考专题4 第3讲课件PPT

这是一份高中数学高考专题4 第3讲课件PPT，共39页。PPT课件主要包含了条件结构，循环结构，复数的有关概念，复数代数形式的运算，专题复习检测等内容，欢迎下载使用。

2．(2019年新课标Ⅲ)z(1＋i)＝2i，则z＝(　　)A．－1－i　B．－1＋iC．1－i　D．1＋i【答案】D
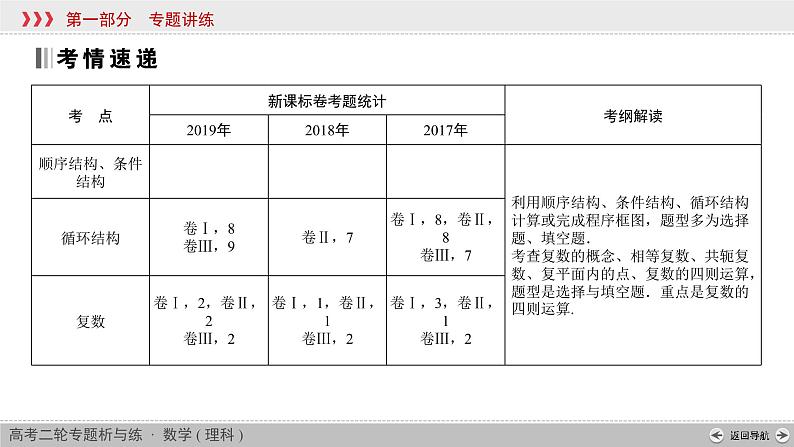
一、程序框图的三种基本结构1．顺序结构顺序结构是最简单的算法结构，语句与语句之间、框与框之间是按从上到下顺序进行的．程序框图中一定包含顺序结构．2．条件结构当需要对研究对象进行逻辑判断时，要使用条件结构，它是根据指定条件选择执行不同指令的控制结构．
3．循环结构两种循环结构的特点直到型循环结构：在执行了一次循环体后，对条件进行判断，如果条件不满足，就继续执行循环体，直到条件满足时终止循环．当型循环结构：在每次执行循环体前，对条件进行判断，当条件满足时，执行循环体，否则终止循环．
二、复数的有关概念1．定义形如a＋bi(a，b∈R)的数叫作复数，其中a叫作实部，b叫作虚部(i为虚数单位)．2．分类
例1 执行下面的程序框图，当输入的x的值为4时，输出的y的值为2，则空白判断框中的条件可能为(　　)A．x＞3？　B．x＞4？　　C．x≤4？　D．x≤5?【答案】B【解析】输入x的值为4时，由x＋2＝6，lg24＝2可知x＝4不满足判断框中的条件，只能是“x＞4？”．故选B．
应用顺序结构和条件结构的注意点：(1)顺序结构：顺序结构是最简单的算法结构，语句与语句之间、框与框之间是按从上到下的顺序进行的．(2)条件结构：利用条件结构解决算法问题时，重点是判断框，判断框内的条件不同，对应的下一图框中的内容和操作要相应地进行变化，故要重点分析判断框内的条件是否满足．
例2 (2018年江西南昌一模)执行如图所示的程序框图，若输出的n＝9，则输入的整数P的最小值是(　　 )A．50　B．77　　C．78　D．306【分析】根据程序框图进行模拟计算即可．【答案】C
【解析】模拟程序框图的运行过程如下：n＝1，S＝0，输入P，S＝0＋2＝2，n＝2，S≤P；S＝2＋22＝6，n＝3，S≤P；S＝－6＋23＝2，n＝4，S≤P；S＝2＋24＝18，n＝5，S≤P；S＝－18＋25＝14，n＝6，S≤P；S＝14＋26＝78，n＝7，S≤P；S＝－78＋27＝50，n＝8，S≤P；S＝50＋28＝306，n＝9，S>P；终止循环，输出n＝9.所以P的最小值为78.
1．解决程序框图问题要注意几个常用变量：(1)计数变量：用来记录某个事件发生的次数，如i＝i＋1.(2)累加变量：用来计算数据之和，如S＝S＋i.(3)累乘变量：用来计算数据之积，如p＝p×i.2．处理循环结构的框图问题，关键是理解并认清终止循环结构的条件及循环次数．
3．两种循环结构的特点．直到型循环结构：在执行了一次循环体后，对条件进行判断，如果条件不满足，就继续执行循环体，直到条件满足时终止循环．当型循环结构：在每次执行循环体前，对条件进行判断，当条件满足时，执行循环体，否则终止循环．
(1)(2018年北京)执行如图所示的程序框图，输出的s值为(　　)
解决复数概念问题的方法及注意事项：(1)复数的分类及对应点的位置问题都可以转化为复数的实部与虚部应该满足的条件问题，只需把复数化为代数形式，列出实部和虚部满足的方程(不等式)组即可．(2)解题时一定要先看复数是否为a＋bi(a，b∈R)的形式，以确定实部和虚部．
设(1＋3i)(a－i)的实部与虚部相等，其中a为实数，则a＝(　　)A．－3　B．－2　　C．2　D．3【答案】C【解析】(1＋3i)(a－i)＝(a＋3)＋(3a－1)i，由已知可得a＋3＝3a－1，解得a＝2.
例4 已知复数z＝(1＋i)(1＋2i)，其中i是虚数单位，则z的模是__________．【分析】利用复数代数形式的运算及模的运算法则计算．
复数代数形式运算问题的解题策略：(1)复数的乘法．复数的乘法类似于多项式的乘法运算，可将含有虚数单位i的看作一类同类项，不含i的看作另一类同类项，分别合并即可．(2)复数的除法．除法的关键是分子、分母同乘以分母的共轭复数，解题中要注意把i的幂写成最简形式．
4．复数z1，z2在复平面内对应的点关于直线y＝x对称且z1＝3＋2i，则z2＝(　　)A．3－2i　B．2－3iC．－3－2i　D．2＋3i【答案】D【解析】复数z1在复平面内对应的点为(3,2)，其关于直线y＝x对称的点为(2,3)，表示的复数z2＝2＋3i.故选D．