专训27.1.3 相似多边形的判定和性质-简单数学之九年级下册考点专训（人教版） 试卷

这是一份专训27.1.3 相似多边形的判定和性质-简单数学之九年级下册考点专训（人教版），文件包含专训2713相似多边形的判定和性质-简单数学之九年级下册考点专训解析版人教版docx、专训2713相似多边形的判定和性质-简单数学之九年级下册考点专训原卷版人教版docx等2份试卷配套教学资源，其中试卷共40页， 欢迎下载使用。
专训27.1.3 相似多边形的判定和性质
一、单选题
1．（2021·全国·九年级课时练习）已知矩形中，，下列四个矩形中与矩形相似的是（ ）
A． B． C． D．
【答案】A
【分析】
利用相似多边形对应边的比相等，即可找出结论．
【详解】
解：∵，∴A选项中的矩形与矩形ABCD相似，该选项正确；
∵，∴B选项中的矩形与矩形ABCD不相似，该选项错误；
∵，∴C选项中的矩形与矩形ABCD不相似，该选项错误；
∵，∴D选项中的矩形与矩形ABCD不相似，该选项错误．
故选A．
【点睛】
本题考查了相似多边形的性质，牢记“相似多边形对应边的比相等”是解题的关键．
2．（2020·山东北区·九年级期末）如图，细线平行于正多边形一边，并把它分割成两部分，则阴影部分多边形与原多边形相似的是（ ）
A． B． C． D．
【答案】A
【分析】
利用相似多边形的判定方法判断即可．
【详解】
解：A、阴影三角形与原三角形的对应角相等、对应边的比相等，符合相似多边形的定义，符合题意；
B、阴影矩形与原矩形的对应角相等，但对应边的比不相等，不符合相似多边形的定义，不符合题意；
C、阴影五边形与原五边形的对应角相等，但对应边的比不相等，不符合相似多边形的定义，不符合题意；
D、阴影六边形与原六边形的对应角相等，但对应边的比不相等，不符合相似多边形的定义，不符合题意；
故选：A．
【点睛】
本题考查了相似多边形的定义，解题的关键是了解相似多边形的对应角相等，对应边的比相等．
3．（2021·全国·九年级课时练习）如图，取一张长为a，宽为b的长方形纸片，将它对折两次后得到一张小长方形纸片，若要使小长方形与原长方形相似，则原长方形纸片的边a、b应满足的条件是（ ）

A．a＝b B．a＝2b C．a＝2b D．a＝4b
【答案】B
【分析】
根据对折表示出小长方形的长和宽，再根据相似多边形的判定，对应边成比例列式计算即可．
【详解】
解：对折两次后的小长方形的长为b，宽为，
要使小长方形与原长方形相似，只要满足即可，
∴．
故选：B．
【点睛】
本题考查了相似多边形的判定，准确表示出小长方形的长和宽是解题的关键．
4．（2021·河北·九年级专题练习）将矩形按照如图所示的方式向外扩张得到新矩形，每条对角线向其延长线两个方向各延伸，若所得新矩形与原矩形相似，则的值的个数可以是（ ）

A．1 B．2 C．3 D．无数个
【答案】D
【分析】
根据相似多边形的对应边成比例，对应角相等进行分析判断．
【详解】
新矩形与原矩形相似，因此可得到对应边成比例，对应角相等，与a的取值无关，
故选：D．
【点睛】
本题考查了相似多边形的判定，矩形性质的应用，能理解相似多边形的判定定理是解此题的关键．
5．（2020·河北保定师范附属学校九年级期中）如图，在矩形、三角形、正五边形、菱形的外边加一个宽度一样的外框，保证外框的边界与原图形对应边平行，则外框与原图一定相似的有（ ）

A．1个 B．2个 C．3 D．4个
【答案】C
【分析】
根据相似多边形的判定定理对各个选项进行分析，从而确定最后答案．
【详解】
矩形的原图与外框不相似，因为其对应角的度数一定相同，但对应边的比值不一定相等，不符合相似的条件；
锐角三角形的原图与外框相似，因为其对应角均相等，对应边均对应成比例，符合相似的条件；
正五边形相似，因为它们的边长都对应成比例、对应角都相等，符合相似的条件；
菱形的原图与外框相似，因为其对应角均相等，对应边均对应成比例，符合相似的条件．
综上，外框与原图一定相似的有3个，
故选：C．
【点睛】
本题主要考查了相似图形的概念，注意边数相同、各角对应相等、各边对应成比例的两个多边形是相似多边形．
6．（2021·河南·郑州中原一中实验学校九年级月考）如图，将一张矩形纸片沿它的长边折叠两次（EF、GH为折痕），得到三个全等的小矩形，如果小矩形与原来的矩形相似，那么小矩形的长边与短边的比是（ ）

A． B． C．2：1 D．3：1
【答案】B
【分析】
先分别表示出对折前后的矩形的长和宽，再根据小矩形与原来的矩形相似可得对应边成比例，由此列出比例式求解即可．
【详解】
解：设原来矩形的长为，宽为，
则对折后的小矩形的长为，宽为，
得到的三个全等的小矩形都和原矩形相似，
，
，
（舍负），
∴．
故选：B．
【点睛】
此题主要考查了相似多边形的性质，关键是掌握相似多边形对应边成比例．
7．（2021·辽宁·沈阳市光明中学九年级月考）如图，一张矩形纸片沿它的长边AD对折（折痕为EF），得到两个全等的小矩形，若小矩形与原来的矩形相似，那么原来矩形的长边与短边之比为（　　）

A．1：1 B．：1 C．：1 D．2：1
【答案】B
【分析】
设原来矩形的长为x，宽为y，表示出对折后的矩形的长和宽，再根据相似矩形对应边成比例列出比例式，然后求解．
【详解】
解：设原来矩形的长为x，宽为y，
则对折后的矩形的长为y，宽为，
∵得到的两个矩形都和原矩形相似，
∴x：y＝y：，
解得，（负值舍去）
∴x：y＝：1．
故选：B．
【点睛】
此题主要考查了相似多边形的性质，关键是掌握相似多边形对应边成比例，列出比例式求值．
8．（2021·全国·九年级专题练习）如图，矩形ABCD∽矩形FAHG，连结BD，延长GH分别交BD、BC于点Ⅰ、J，延长CD、FG交于点E，一定能求出△BIJ面积的条件是（　　）

A．矩形ABJH和矩形HJCD的面积之差
B．矩形ABJH和矩形HDEG的面积之差
C．矩形ABCD和矩形AHGF的面积之差
D．矩形FBJG和矩形GJCE的面积之差
【答案】B
【分析】
设矩形的边AH＝x，GH＝y，EG＝a，DC＝b，根据平行线分线段成比例可得JI＝，根据相似多边形的性质可得＝，然后表示出S阴影的面积和S矩形ABJH﹣S矩形HDEG的值即可求解．
【详解】
解：设矩形的边AH＝x，GH＝y，EG＝a，DC＝b，
则BJ＝x，JC＝a，
∵JI//CD，
∴＝即JI＝，
∵矩形ABCD∽矩形FAHG，
∴＝，
即＝，
∴x+a＝，
∴S阴影＝BJ•JI
＝x•
＝xy．
∵S矩形ABJH﹣S矩形HDEG
＝xb﹣ay
＝x•﹣ay
＝xy．
∴S阴影△BIJ＝(S矩形ABJH﹣S矩形HDEG)．
所以一定能求出△BIJ面积的条件是矩形ABJH和矩形HDEG的面积之差．
故选：B．
【点睛】
本题考查了相似多边形的性质、三角形的面积、矩形的性质，解决本题的关键是掌握相似多边形的性质．
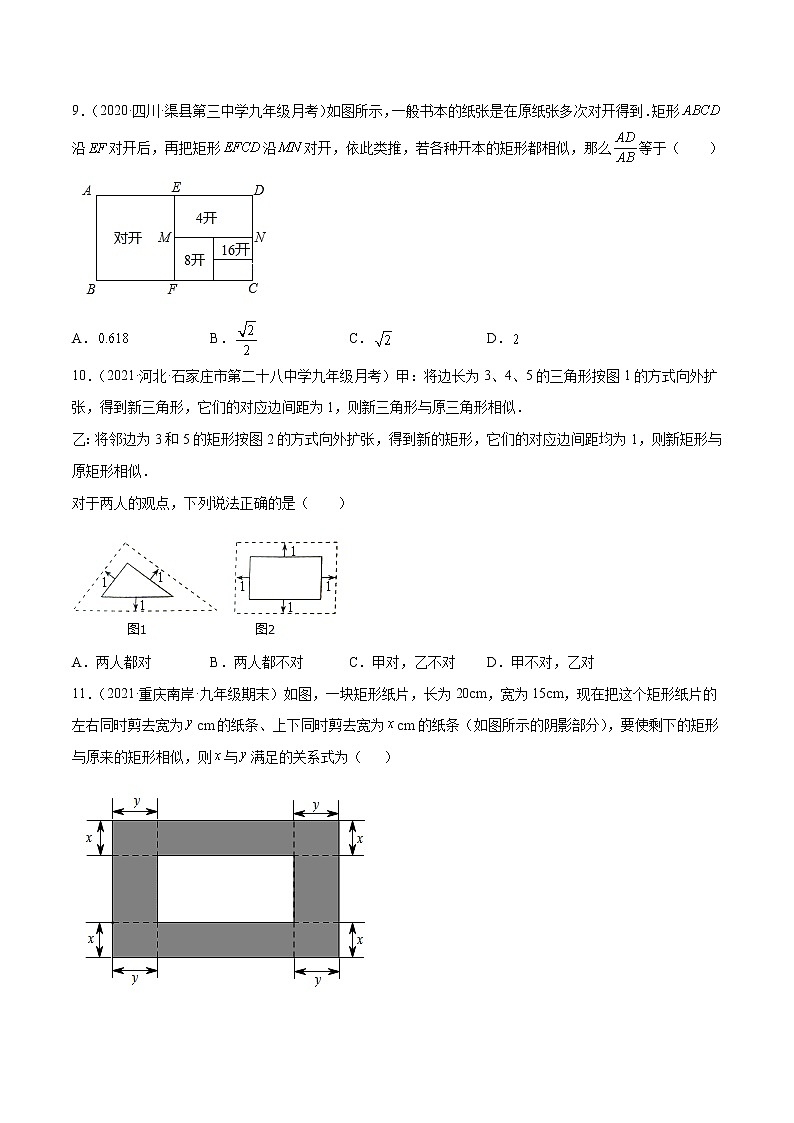
9．（2020·四川·渠县第三中学九年级月考）如图所示，一般书本的纸张是在原纸张多次对开得到．矩形沿对开后，再把矩形沿对开，依此类推，若各种开本的矩形都相似，那么等于（　　）

A． B． C． D．
【答案】C
【分析】
根据矩形ABCD的面积是矩形ABFE面积的2倍，得出相似图形面积比是相似比的平方，进而得出的值．
【详解】
解：∵矩形ABCD的面积是矩形ABFE面积的2倍，各种开本的矩形都相似，
∴（）2=2，
∴=．
故选：C．
【点睛】
本题考查的是相似多边形的性质，即相似多边形面积的比等于相似比的平方．
10．（2021·河北·石家庄市第二十八中学九年级月考）甲：将边长为3、4、5的三角形按图1的方式向外扩张，得到新三角形，它们的对应边间距为1，则新三角形与原三角形相似．
乙：将邻边为3和5的矩形按图2的方式向外扩张，得到新的矩形，它们的对应边间距均为1，则新矩形与原矩形相似．
对于两人的观点，下列说法正确的是（ ）

A．两人都对 B．两人都不对 C．甲对，乙不对 D．甲不对，乙对
【答案】C
【分析】
甲：根据题意得：AB∥A′B′，AC∥A′C′，BC∥B′C′，即可证得∠A=∠A′，∠B=∠B′，可得△ABC∽△A′B′C′；
乙：根据题意得：AB=CD=3，AD=BC=5，则A′B′=C′D′=3+2=5，A′D′=B′C′=5+2=7，则可得，即新矩形与原矩形不相似．
【详解】
解：甲：根据题意得：AB∥A′B′，AC∥A′C′，BC∥B′C′，
∴∠A=∠A′，∠B=∠B′，
∴△ABC∽△A′B′C′，
∴甲说法正确；
乙：∵根据题意得：AB=CD=3，AD=BC=5，则A′B′=C′D′=3+2=5，A′D′=B′C′=5+2=7，
∴，
∴，
∴新矩形与原矩形不相似．
∴乙说法不正确．
故选：C．
【点睛】
此题考查了相似三角形以及相似多边形的判定．此题难度不大，注意掌握数形结合思想的应用．
11．（2021·重庆南岸·九年级期末）如图，一块矩形纸片，长为20cm，宽为15cm，现在把这个矩形纸片的左右同时剪去宽为cm的纸条、上下同时剪去宽为cm的纸条（如图所示的阴影部分），要使剩下的矩形与原来的矩形相似，则与满足的关系式为（ ）


A． B． C． D．
【答案】D
【分析】
根据题意，剩下矩形与原矩形相似，利用相似形的对应边的比相等可得．
【详解】
解：依题意，要使剩下的矩形与原来的矩形相似，
则
15（20-2y）=20(15-2x)
3（20-2y）=4(15-2x)
60-6y=60-8x
-6y=-8x
3y=4x
即．
故选：D．
【点睛】
本题考查了相似形的对应边的比相等，分清矩形的对应边是解决本题的关键．
12．（2021·浙江浙江·九年级月考）如图，矩形的四个顶点分别在菱形的四条边上，．将，分别沿边，折叠，当重叠部分为菱形且面积是菱形面积的时，则为（ ）

A． B．2 C． D．
【答案】D
【分析】
设重叠的菱形边长为x，BE=BF=y，由矩形和菱形的对称性以及折叠的性质得：四边形AHME、四边形BENF是菱形，得出EN=BE=y，EM=x+y，由相似的性质得出AB=4MN=4x，求出AE=AB-BE=4x-y，得出方程4x-y=x+y，得出x=y，AE=y，即可得出结论．
【详解】
解：设重叠的菱形边长为x，BE=BF=y，
由矩形和菱形的对称性以及折叠的性质得：四边形AHME、四边形BENF是菱形，
∴AE=EM，EN=BE=y，EM=x+y，
∵当重叠部分为菱形且面积是菱形ABCD面积的，且两个菱形相似，
∴AB=4MN=4x，
∴AE=AB-BE=4x-y，
∴4x-y=x+y，
解得：x=y，
∴AE=y，
∴，
∴，
故选：D．

【点睛】
本题考查了折叠的性质、菱形的判定与性质、矩形的性质、相似多边形的性质等知识；熟练掌握菱形的判定与性质是解决问题的关键，学会利用参数解决问题．


二、多选题
13．（2021·全国·九年级专题练习）如图，在矩形、锐角三角形、正五边形、直角三角形的外边加一个宽度一样的外框，保证外框的边与原图形的对应边平行，则外框与原图一定相似的有（　 　）
A． B． C． D．
【答案】BCD
【分析】
根据相似多边形的判定定理对各个选项进行分析，从而确定最后答案．
【详解】
解：矩形不相似，因为其对应角的度数一定相同，但对应边的比值不一定相等，不符合相似的条件，故A不符合题意；
锐角三角形、正五边形、直角三角形的原图与外框相似，因为其对应角均相等，对应边均对应成比例，符合相似的条件，故B、C、D符合题意．
故选BCD．
【点睛】
此题主要考查了相似图形判定，注意边数相同、各角对应相等、各边对应成比例的两个多边形是相似多边形．

三、填空题
14．（2021·广东顺德·九年级月考）如图，在矩形ABCD中，AD＞AB，AB＝2．点E在矩形ABCD的边BC上，连结AE，将矩形ABCD沿AE翻折，翻折后的点B落在边AD上的点F处，得到矩形CDFE．若矩形CDFE与原矩形ABCD相似，则AD的长为__．

【答案】
【分析】
根据相似多边形的性质列出比例式，计算即可．
【详解】
∵矩形CDFE∽矩形ADCB，
∴＝，即＝，
整理得，AD2﹣2AD﹣4＝0，
解得，AD1＝1﹣（舍去），AD2＝，
故答案为：．
【点睛】
本题考查的是相似多边形的性质，掌握相似多边形的对应边成比例是解题的关键．
15．（2021·山西·太原市志达中学校九年级月考）复印纸型号多样，而各型号复印纸之间存在这样的关系：将其中一型号纸张（如A3纸）沿较长边中点的连线对折，就能得到下一型号（A4纸）的纸张，且对折得到的两个矩形和原来的矩形相似（即A3纸与A4纸相似），则这些型号的复印纸宽与长之比为________．

【答案】
【分析】
设这些型号的复印纸的长、宽分别为b、a，根据相似多边形的对应边的比相等列出比例式，计算即可．
【详解】
解：设这些型号的复印纸的长、宽分别为、，
得到的矩形都和原来的矩形相似，
，则，
，
故答案为：．
【点睛】
本题考查的是相似多边形的性质，相似多边形的性质为：①对应角相等；②对应边的比相等．
16．（2021·山西孝义·九年级期末）如图所示，复印纸的型号有A0，A1，A2，A3，A4等，它们之间存在着这样一种关系：将其中某一型号（如A3）的复印纸沿较长边的中点对折，就能得到两张下一型号（A4）的复印纸，且得到的两个矩形都和原来的矩形相似，那么这些型号的复印纸的长、宽之比为______．

【答案】
【分析】
设这些型号的复印纸的长、宽分别为b、a，根据相似多边形的对应边的比相等列出比例式，计算即可．
【详解】
解：设这些型号的复印纸的长、宽分别为b、a，
∵得到的矩形都和原来的矩形相似，
∴，
则，
∴，
∴这些型号的复印纸的长宽之比为，
故答案为：．
【点睛】
本题考查的是相似多边形的性质，相似多边形的性质为：①对应角相等；②对应边的比相等．
17．（2021·上海·九年级专题练习）如图，在矩形ABCD中，AD=2，CD=1，连接AC，以对角线AC为边，按逆时针方向作矩形ABCD的相似矩形AB1C1C，再连接AC1，以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1，…，按此规律继续下去，则矩形AB4C4C3的面积为_____．

【答案】
【分析】
利用勾股定理可求得AC的长，根据面积比等于相似比的平方可得矩形AB1C1C的面积，同理可求出矩形AB2C2C1、AB3C3C2，……的面积，从而可发现规律，根据规律即可求得第n个矩形的面积，继而即可求得矩形AB4C4C3的面积．
【详解】
∵在矩形ABCD中，AD=2，CD=1，
∴AC=，
∵矩形ABCD与矩形AB1C1C相似，
∴矩形AB1C1C与矩形ABCD的相似比为，
∴矩形AB1C1C与矩形ABCD的面积比为，
∵矩形ABCD的面积为1×2=2，
∴矩形AB1C1C的面积为2×=，
同理：矩形AB2C2C1的面积为×==，
矩形AB3C3C2的面积为×==，
……
∴矩形ABnCnCn-1面积为，
∴矩形AB4C4C3的面积为=，
故答案为：
【点睛】
本题考查了矩形的性质，勾股定理，相似多边形的性质，根据求出的结果得出规律并熟记相似图形的面积比等于相似比的平方是解题关键．

四、解答题
18．（2021·全国·九年级课时练习）先判断下列各命题的真假，然后写出它们的逆命题，并判断逆命题的真假：
（1）对角线互相垂直的四边形是菱形；
（2）相似四边形对应边成比例．
【答案】（1）原命题是假命题；逆命题：菱形的对角线互相垂直；逆命题是真命题；（2）原命题是真命题；逆命题：四条边分别对应成比例的四边形是相似四边形；逆命题是假命题．
【分析】
（1）先利用举反例的方法判断原命题是假命题，再把原命题的题设与结论交换位置可得命题的逆命题，再利用菱形的性质可得其逆命题是真命题，从而可得答案；
（2）先利用相似多边形的性质可得原命题是真命题，再把原命题的题设与结论交换位置可得其逆命题，再利用举反例的方法可得其逆命题是假命题，从而可得答案.
【详解】
解：（1）如图：

所以：命题：“对角线互相垂直的四边形是菱形”是假命题，
“对角线互相垂直的四边形是菱形”的逆命题是：
菱形的对角线互相垂直，由菱形是轴对称图形可得：其逆命题是真命题，
（2）由相似多边形的对应边成比例可得：
命题“相似四边形对应边成比例．”是真命题，
“相似四边形对应边成比例”的逆命题是：
四条边分别对应成比例的四边形是相似四边形，
如图：

菱形与正方形的四条边对应成比例，而四个角不对应相等，所以两个图形不相似，
“相似四边形对应边成比例”其逆命题是假命题.
【点睛】
本题考查的命题的逆命题，命题的真假判断，掌握举反例判断命题是假命题是解本题的关键.
19．（2021·全国·九年级课时练习）如图，矩形草坪长、宽．沿草坪四周有宽的环行小路，小路内外边缘形成的两个矩形相似吗？说出你的理由．

【答案】不相似．小路内外边缘形成的两个矩形的边长分别为30，20和28，18．因为，，即这两个矩形的边不成比例，所以它们不相似
【分析】
根据已知条件，可求出小路内侧矩形的长和宽分别为28，8；再把两个矩形的边分两种情况进行比值运算，结果，，即可得出答案．
【详解】
解：不相似．理由如下：
因为草坪四周有宽的环行小路，
所以小路内外边缘形成的两个矩形的边长分别为30，20和28，18；
因为，，即这两个矩形的边不成比例，
所以它们不相似．
【点睛】
本题主要考查了相似图形的判定，即不仅要对应角相等，还要对应边成比例．
20．（2021·全国·九年级课时练习）如图，四边形是矩形，点F在对角线AC上运动，，．四边形和四边形一直保持相似吗？证明你的结论．

【答案】四边形与四边形一直保持相似．原因是它们的角分别相等、边成比例．
【分析】
由，证明再证明四个角分别对应相等，四条边分别对应成比例，从而可得答案.
【详解】
解： ，，

即
，，




四边形与四边形一直保持相似．
【点睛】
本题考查的是四边形相似的判定，掌握“四个角分别对应相等，四条边分别对应成比例的两个四边形相似”是解题的关键.
21．（2021·全国·九年级课时练习）图中每组两个矩形相似吗？说说你的理由．

【答案】第（1）组的两个矩形相似；第（2）组的两个矩形不相以，证明见解析．
【分析】
利用相似多边形的判定定理进行证明即可．
【详解】
解：第（1）组的两个矩形相似；
，
第（1）组的两个矩形相似；
，
第（2）组的两个矩形不相似．
【点睛】
本题考查了相似多边形的判定定理，解题的关键是掌握相应的判定定理．
22．（2021·全国·九年级课时练习）如图所示的两个五边形相似，求a，b，c，d的值．

【答案】，，，
【分析】
根据相似多边形的性质求解即可；
【详解】
∵两个五边形相似，
∴相似比是，
∴，
解得，，，．
【点睛】
本题主要考查了利用相似多边形的性质应用，准确计算是解题的关键．
23．（2021·全国·九年级课时练习）如图，一块矩形绸布的长，宽，按照图中所示的方式将它裁成相同的三面矩形彩旗，且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同，即，那么a的值应当是多少？

【答案】
【分析】
由裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同，构建方程求解即可．
【详解】
解：根据题意可知，．
由，得，
即．
∴．
开平方，得（舍去）．
【点睛】
此题考查了相似多边形的性质．注意相似多边形的对应边成比例．
24．（2021·全国·九年级课时练习）如图，将一张矩形纸片沿它的长边对折（为折痕），得到两个全等的小矩形．如果小矩形长边与短边的比等于原来矩形长边与短边的比，那么原来矩形的长边与短边的比是多少？


【答案】原来矩形长边与短边的比为．
【分析】
先根据题意得到，再代入变形得到，然后求解．
【详解】
根据题意，得．
将代入，得，开平方得（舍去）．
【点睛】
本题主要利用相似多边形对应边成比例的性质，需要熟练掌握．
25．（2021·山东张店·八年级期末）如图，四边形四边形，且，，，，，，．

（1）请直接写出：______度；
（2）求边和的长．
【答案】（1）83；（2）AB＝，BC＝12．
【分析】
（1）根据相似多边形的对应角相等以及四边形内角和360°解决问题即可．
（2）利用相似多边形的对应边成比例，解决问题即可．
【详解】
解：（1）∵四边形ABCD∽四边形A′B′C′D′，
∴∠D＝∠D′＝140°，
∴∠C＝360°−∠A−∠B−∠D＝360°−62°−75°−140°＝83°，
故答案为：83；
（2）∵四边形ABCD∽四边形A′B′C′D′，
∴，
∴，
∴AB＝，BC＝12．
【点睛】
本题考查相似多边形的性质，四边形内角和定理等知识，解题的关键是掌握相似多边形的性质，灵活运用所学知识解决问题．
26．（2021·全国·九年级课时练习）如图，四边形和相似，求角的大小和的长度x．

【答案】α＝83°，β＝81°，x＝28．
【分析】
根据相似多边形的对应角相等可得出α＝∠C＝83°，∠F＝∠B＝78°，再根据四边形的内角和等于360°可计算求出β的大小，然后根据相似多边形的对应边成比例即可求出EH的长度x．
【详解】
解：∵四边形ABCD与四边形EFGH相似，
∴α＝∠C＝83°，∠F＝∠B＝78°，EH：AD＝EF：AB，
∴x：21＝24：18，解得x＝28．
在四边形EFGH中，β＝360°﹣83°﹣78°﹣118°＝81°．
∴∠G＝∠C＝67°．
故α＝83°，β＝81°，x＝28．
【点睛】
本题考查了相似多边形的对应角相等，对应边成比例的性质，四边形的内角和等于360°，熟记性质并熟练运用是求解的关键．
27．（2021·全国·九年级课时练习）如图，矩形草坪的长为a米，宽为b米（），沿草坪四周外围有宽为x米的环形小路．

（1）草坪的长与宽的比值________，外围矩形的长与宽的比值________；（用含有a、b、x的代数式表示）
（2）请比较m与n的大小；
（3）图中的两个矩形相似吗？为什么？
【答案】（1）， ；（2）；（3）图中的两个矩形不相似，见解析
【分析】
（1）根据即可求解出m的值，然后分别求出外围矩形的长为a+2x，宽为b+2x由此求解即可；
（2）利用作差法进行求解即可得到答案；
（3）假设两个矩形相似那么m=n与事实矛盾，由此即可得到答案．
【详解】
解：（1）∵矩形草坪的长为a米，宽为b米，
∴草坪的长与宽的比值，外围矩形的长与宽的比值；
（2）

，
∵，
∴，
∴；
（3）若图中的两个矩形相似，则，
∵，
∴图中的两个矩形不相似．
【点睛】
本题主要考查了假设法，分式的混合运算，相似图形的性质，解题的关键在于能够熟练掌握相关知识进行求解．
28．（2020·浙江·台州市路桥区桐屿镇中学九年级月考）某校九年级数学兴趣小组在探究相似多边形问题时，他们提出了下面两个观点：
观点一：将外面大三角形按图1的方式向内缩小，得到新三角形，它们对应的边间距都为1，则新三角形与原三角形相似．
观点二：将邻边为6和10的矩形按图2的方式向内缩小，得到新的矩形，它们对应的边间距都为1，则新矩形与原矩形相似．

请回答下列问题：
（1）你认为上述两个观点是否正确？请说明理由．
（2）如图3，已知，AC=6，BC=8，AB=10，将按图3的方式向外扩张，得到，它们对应的边间距都为1，DE=15，求的面积．
【答案】（1）观点一正确；观点二不正确；理由见解析；（2）54
【分析】
（1）根据相似三角形以及相似多边形的判定定理来判定两个观点是否正确；
（2）首先根据勾股定理的逆定理求出∠C是直角，根据相似三角形的性质可求出△DEF的边长，进而求出△DEF的面积．
【详解】
解：（1）观点一正确；观点二不正确．
理由：①如图（1）连接并延长DA，交FC的延长线于点O，

∵△ABC和△DEF对应的边的距离都为1，
∴AB//DE，AC//DF，
∴∠FDO＝∠CAO，∠ODE＝∠OAB，
∴∠FDO+∠ODE＝∠CAO+∠OAB，
即∠FDE＝∠CAB，同理∠DEF＝∠ABC，
∴△ABC∽△DEF，
∴观点一正确；
②如图（2）由题意可知，原矩形的邻边为6和10，

则新矩形邻边为4和8，
∵，，
∴，
∴新矩形于原矩形不相似，
∴观点二不正确；
（2）∵AC＝6，BC＝8，AB＝10，
∴△ABC是直角三角形，
∴∠ACB=90°，
由（1）知△ABC∽△DEF，
∴∠DFE=90°，，
∴，，
∴DF＝9，EF＝12，
∴△DEF的面积为：9×12＝54．
【点睛】
本题主要考查了相似形的综合题，矩形的性质，平行线的判定，主要涉及到相似三角形以及相似多边形的判定，熟练应用相似三角形的判定与性质是解题关键．
29．（2021·全国·九年级专题练习）如图1，矩形ODEF的一边落在矩形ABCO的一边上，并且矩形ODEF∽矩形ABCO，其相似比为1：4，矩形ABCO的边AB=4，BC=4．
（1）求矩形ODEF的面积；
（2）将图1中的矩形ODEF绕点O逆时针旋转一周，连接EC、EA，ACE的面积是否存在最大值或最小值？若存在，求出最大值或最小值；若不存在，请说明理由．

【答案】（1）；（2）存在，最大值，最小值
【分析】
（1）根据相似多边形面积的比等于相似比的平方求解即可；
（2）旋转一周，点E的轨迹是以点O为圆心以2为半径的圆，所以△ACE的AC边上的高就是点E到AC的距离，也就是AC到圆上的点的距离，又最大值和最小值，最大值为点O到AC的距离与圆的半径的和，最小值为点O到AC的距离与圆的半径的差，再利用三角形的面积公式求解即可．
【详解】
解：（1）∵矩形ODEF∽矩形ABCO，其相似比为1：4，
∴S矩形ODEF=S矩形ABCO=×4×4=；
（2）存在．
∵OE=，
所以点E的轨迹为以点O为圆心，以2为半径的圆，
设点O到AC的距离为h，
AC=，
∴8h=4×4，
解得h=2，
∴当点E到AC的距离为2+2时，△ACE的面积有最大值，
当点E到AC的距离为2-2时，△ACE的面积有最小值，
S最大=，
S最小=．
【点睛】
本题主要考查了相似多边形的性质，矩形的性质，勾股定理，圆上的点到直线的距离的取值范围，理解AC边上的高的最大值为点O到AC的距离与圆的半径的和是解本题的关键．
30．（2021·全国·九年级）下面我们做一次折叠活动：第一步：在一张宽为2的矩形纸片的一端，利用图1的方法折叠出一个正方形，然后把纸片展开．
第二步：如图（2），把这个正方形折成两个相等的矩形，再把纸片展平．
第三步：折出内侧矩形的对角线AB，并将AB折到图（3）中所示的AD处．
第四步：展平纸片，按照所得的点D折出DE，矩形BCDE就是黄金矩形，你能说明为什么吗？（注：当矩形的宽与长的比为时，称这个矩形为黄金矩形）

【答案】答案见解析
【分析】
设正方形BCNM的边长为2，利用对折的性质得ACNC＝1，再在△ABC中根据勾股定理计算出AB，接着利用对折得AD＝AB，所以CD＝AD﹣AC＝1，于是有，然后根据黄金矩形的定义进行判断．
【详解】
解：由题意可得正方形BCNM的边长为2，
∵正方形BCNM沿AF对折，
∴ACNC＝1，
在△ABC中，∵BC＝2，AC＝1，
∴AB，
∵AD＝AB，
∴CD＝AD﹣AC＝1，
∴，
∴矩形BCDE就是黄金矩形．
【点评】
本题考查了黄金分割：把线段AB分成两条线段AC和BC（AC＞BC），且使AC是AB和BC的比例中项（即AB：AC＝AC：BC），叫做把线段AB黄金分割，点C叫做线段AB的黄金分割点．其中ACAB≈0.618AB，并且线段AB的黄金分割点有两个．也考查了折叠的性质．