数学九年级下册29.1 投影课后作业题

这是一份数学九年级下册29.1 投影课后作业题，文件包含第二十九章投影与视图验收卷-简单数学之九年级下册考点专训解析版人教版docx、第二十九章投影与视图验收卷-简单数学之九年级下册考点专训原卷版人教版docx等2份试卷配套教学资源，其中试卷共30页， 欢迎下载使用。
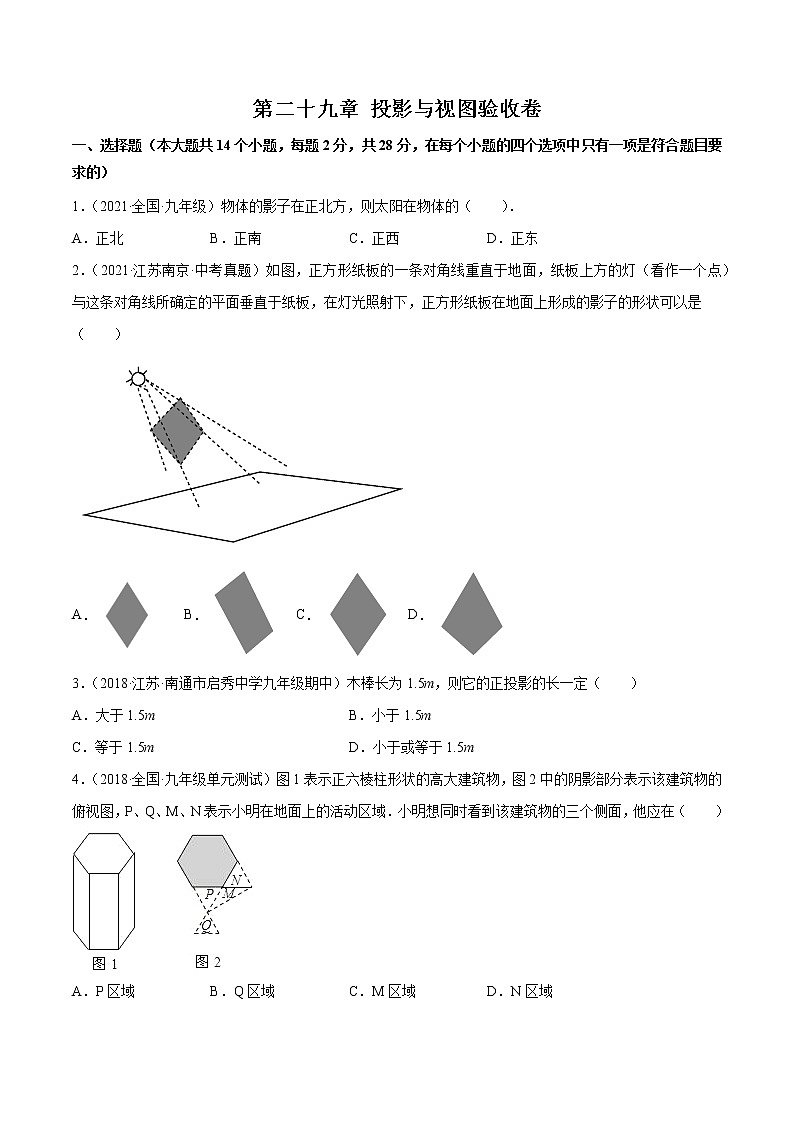
第二十九章 投影与视图验收卷一、选择题（本大题共14个小题，每题2分，共28分，在每个小题的四个选项中只有一项是符合题目要求的）1．（2021·全国·九年级）物体的影子在正北方，则太阳在物体的（    ）．A．正北 B．正南 C．正西 D．正东【答案】B【分析】物体的影子在正北方，则太阳在物体的正南方向，故可求解．【详解】解：∵物体的影子在正北方，∴太阳在物体的正南方．故选：B．【点睛】本题考查了平行投影：由平行光线形成的投影是平行投影，如物体在太阳光的照射下形成的影子就是平行投影．2．（2021·江苏南京·中考真题）如图，正方形纸板的一条对角线重直于地面，纸板上方的灯（看作一个点）与这条对角线所确定的平面垂直于纸板，在灯光照射下，正方形纸板在地面上形成的影子的形状可以是（    ）
A． B． C． D．
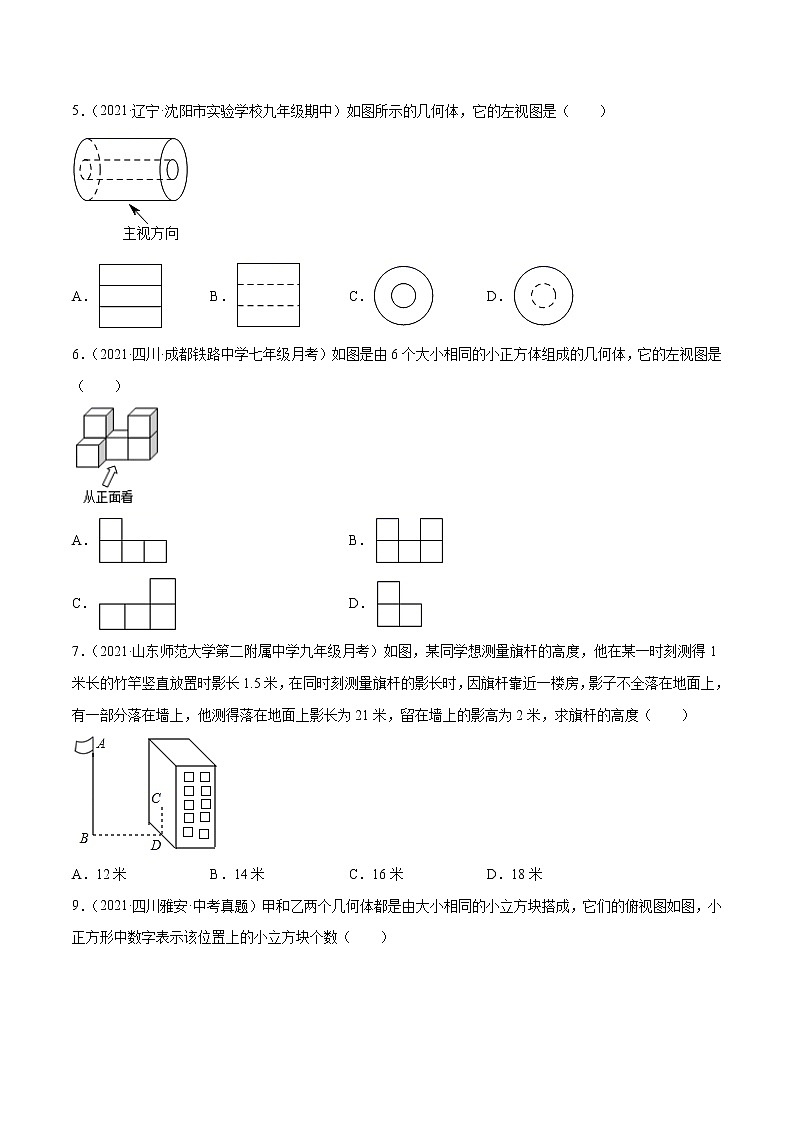
【答案】D【分析】因为中心投影物体的高和影长成比例，正确的区分中心投影和平行投影，依次分析选项即可找到符合题意的选项【详解】因为正方形的对角线互相垂直，且一条对角线垂直地面，光源与对角线组成的平面垂直于地面，则有影子的对角线仍然互相垂直，且由于光源在平板的的上方，则上方的边长影子会更长一些，故选D 【点睛】本题考查了中心投影的概念，应用，利用中心投影的特点，理解中心投影物体的高和影长成比例是解题的关键．3．（2018·江苏·南通市启秀中学九年级期中）木棒长为1.5m，则它的正投影的长一定（　　）A．大于1.5m B．小于1.5mC．等于1.5m D．小于或等于1.5m【答案】D【分析】投影线垂直于投影底幕面时，称正投影，根据木棒的不同位置可得不同的线段长度．【详解】正投影的长度与木棒的摆放角度有关系，但无论怎样摆都不会超过1.5 m．故选D．【点睛】本题考查了正投影的定义，注意同一物体的所处的位置不同得到的正投影也不同．4．（2018·全国·九年级单元测试）图1表示正六棱柱形状的高大建筑物，图2中的阴影部分表示该建筑物的俯视图，P、Q、M、N表示小明在地面上的活动区域．小明想同时看到该建筑物的三个侧面，他应在（　　）A．P区域 B．Q区域 C．M区域 D．N区域【答案】B【详解】根据清视点、视角和盲区的定义，观察图形解决．解：由图片可知，只有Q区域同时处在三个侧面的观察范围内．故选B．5．（2021·辽宁·沈阳市实验学校九年级期中）如图所示的几何体，它的左视图是（　　）A． B． C． D．【答案】C【分析】根据几何体的左面是一个圆环即可得左视图．【详解】由于几何体的左面是一个圆环，故其左视图也是一个圆环，且小圆是实线．故选：C．【点睛】本题考查了三视图，根据所给几何体正确画出三视图是关键．6．（2021·四川·成都铁路中学七年级月考）如图是由6个大小相同的小正方体组成的几何体，它的左视图是（　　）A． B．C． D．【答案】D【分析】细心观察图中几何体中正方体摆放的位置，根据左视图是从左面看到的图形判定则可．【详解】解：从物体左面看，是左边2个正方形，右边1个正方形．
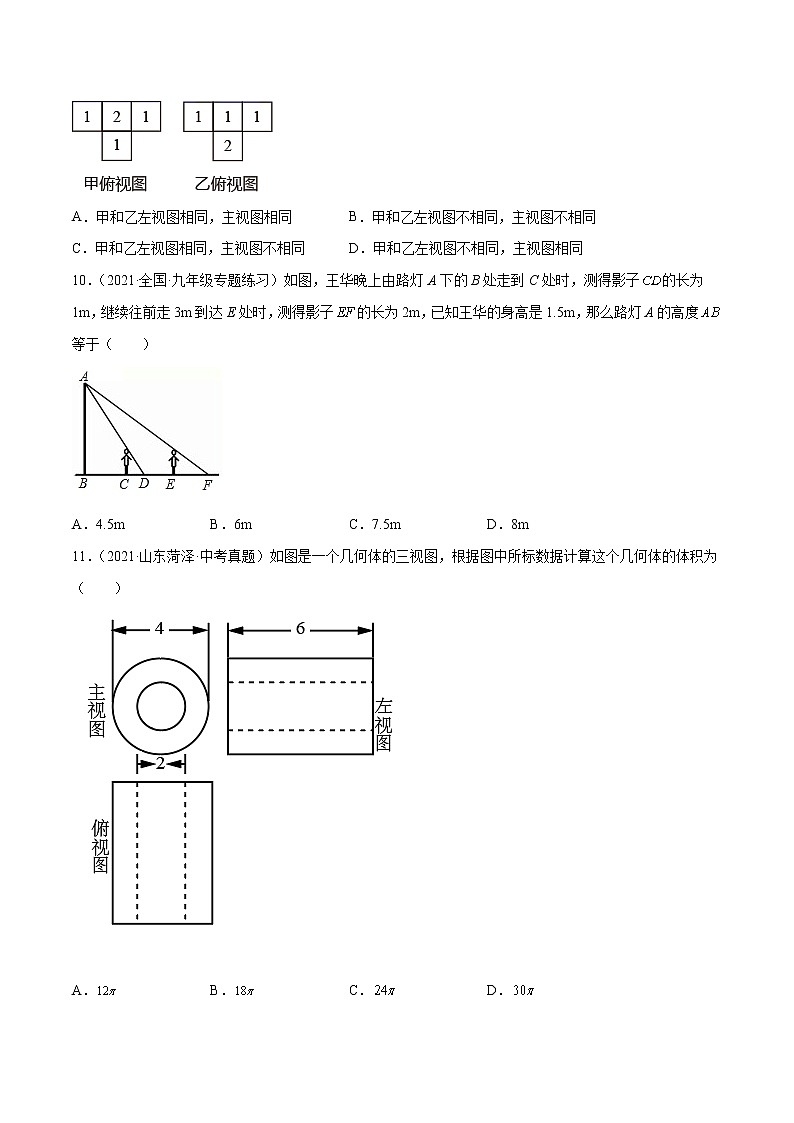
故选：D.．【点睛】本题考查了三视图的知识，左视图是从物体左面看所得到的图形，解答时学生易将三种视图混淆而错误的选其它选项．7．（2021·山东师范大学第二附属中学九年级月考）如图，某同学想测量旗杆的高度，他在某一时刻测得1米长的竹竿竖直放置时影长1.5米，在同时刻测量旗杆的影长时，因旗杆靠近一楼房，影子不全落在地面上，有一部分落在墙上，他测得落在地面上影长为21米，留在墙上的影高为2米，求旗杆的高度（　　）A．12米 B．14米 C．16米 D．18米【答案】C【分析】同一时刻下，不同物体的高度比与影长比相等，画出示意图，找见相似，代入计算即可．【详解】解：如下图：过点C作CE⊥AB于点E，某一时刻竹竿和影长构成的三角形为△FGH，此时FG=1米，GH=1.5米，BD=EC=21米，CD=EB=2米．据题意，同一时刻，∴ ∴∴AE=14∴AB=AE+BE=14+2=16米故选：C【点睛】本题考查平行投影，牢记知识点是解题关键．8．（2021·内蒙古呼伦贝尔·中考真题）根据三视图，求出这个几何体的侧面积（    ）A． B． C． D．【答案】D【分析】由已知，得到几何体是圆柱，由图形数据，得到底面直径以及高，计算侧面积即可．【详解】解：由题意知，几何体是底面直径为10、高为20 的圆柱，所以其侧面积为．故选：D．【点睛】本题考查了由几何体的三视图求几何体的侧面积；关键是还原几何体，明确侧面积的部分．9．（2021·四川雅安·中考真题）甲和乙两个几何体都是由大小相同的小立方块搭成，它们的俯视图如图，小正方形中数字表示该位置上的小立方块个数（    ）A．甲和乙左视图相同，主视图相同 B．甲和乙左视图不相同，主视图不相同C．甲和乙左视图相同，主视图不相同 D．甲和乙左视图不相同，主视图相同【答案】D【分析】根据俯视图，即可判断左视图和主视图的形状．【详解】由甲俯视图知，其左视图为，由乙俯视图知，其左视图为，故它们的左 视图不相同，但它们两个的主视图相同，都是．故选：D．【点睛】本题考查了三视图的知识，关键是根据俯视图及题意确定几何体的形状，从而可确定其左视图和主视图．10．（2021·全国·九年级专题练习）如图，王华晚上由路灯A下的B处走到C处时，测得影子的长为1m，继续往前走3m到达E处时，测得影子的长为2m，已知王华的身高是1.5m，那么路灯A的高度等于（    ）A．4.5m B．6m C．7.5m D．8m【答案】B【分析】根据在同一时刻物高和影长成正比，即在同一时刻的两个物体，影子，经过物体顶部的太阳光线三者构成的两个直角三角形相似解答．【详解】解：如图，，，∴，∴（两个角对应相等的两个三角形相似），∴，设，则，同理，得，∴，∴∴，∴，∴，∴，∴． 故选：B．【点睛】本题综合考查了中心投影的特点和规律以及相似三角形性质的运用．解题的关键是利用中心投影的特点可知在这两组相似三角形中有一组公共边，利用其作为相等关系求出所需要的线段，再求公共边的长度．11．（2021·山东菏泽·中考真题）如图是一个几何体的三视图，根据图中所标数据计算这个几何体的体积为（    ）
 A． B． C． D．【答案】B【分析】根据三视图可以确定该几何体是空心圆柱体，再利用已知数据计算空心圆柱体的体积．【详解】解：先由三视图确定该几何体是空心圆柱体，底面外圆直径是4，内圆直径是2，高是6．空心圆柱体的体积为π×2×6-π×2×6=18π．故选：B．【点睛】本题主要考查由三视图确定几何体和求圆柱体的体积，考查学生的空间想象．12．（2021·山东·青岛市崂山区第三中学七年级期中）由一些相同的小正方体组成的几何体从三个方向看得到的形状图，则组成这个几何体的小正方体最多有多少个，最少有多少个．（   ）A．8， 7 B．9， 7 C．9， 6 D．8，   6【答案】B【分析】从正视图看两列，从左数第一列三层，第二列二层，从左视图看两行，前行三层，后行两层，从俯视图看，几何体由两行两列组成，第一列前行三个小正方体，后行第二列两个小正方体，其他两个位置最少一个正方体，最多两个正方体即可．【详解】解： 从正视图看两列，从左数第一列三层，第二列二层，从左视图看两行，前行三层，后行两层，从俯视图看，几何体由两行两列组成，第一列前行三个小正方体，后行第二列两个小正方体，其他两个位置最少一个正方体，最多两个正方体，组成这个几何体的小正方体最多有3+2+2+2=9个，最少有,3+2+1+1=7个．故选择：B．【点睛】本题考查从不同方向看物体，掌握三视图所看到的图形是解题关键．13．（2020·江苏·无锡市钱桥中学七年级月考）有一个棱长为5的正方体木块，从它的每一个面看都有一个穿透的完全相同的孔（如图中的阴影部分），则这个立体图形的内、外表面的总面积是 (    )A．192 B．216 C．218 D．225【答案】B【分析】根据三视图得出立体图形的表面积即可．【详解】根据图示可得：八个棱长为2的正方体分别在8个顶角，12个棱长为1的正方体分别在12条棱的中间，所以总面积＝（2×2×6）×8＋（1×1×6）×12−4×12＝216．故选B【点睛】此题考查由三视图判断几何体，关键是根据三视图得出几何体的面积．14．（2021·浙江·九年级专题练习）如图为一个用正方体积木搭成的几何体的三视图，俯视图中方格上的数字表示该位置上积木累积的个数．若保证正视图和左视图成立，则a＋b＋c＋d的最大值为（    ）A．12 B．13 C．14 D．15【答案】B【分析】由三视图想象几何体的形状，首先，应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，然后综合起来考虑整体形状，依此即可求解．【详解】解：由正视图第1列和左视图第1列可知a最大为3，由正视图第2列和左视图第2列可知b最大为3，由正视图第3列和左视图第1列和第2列可知c最大为4，d最大为3，则a＋b＋c＋d的最大值为3＋3＋4＋3＝13.故选：B．【点睛】此题考查了由三视图判断几何体，关键看学生对三视图掌握程度和灵活运用能力，同时也体现了对空间想象能力方面的考查，用到的知识点是三视图． 二、填空题（本题共4个小题；每个小题3分，共12分，把正确答案填在横线上）15．（2021·陕西·西安高新一中实验中学九年级月考）如图，在白炽灯下方有一个乒乓球，当乒乓球越接近灯泡时，它在地面上影子的变化情况为____（填“越小”或“越大”，“不变”）【答案】越大【分析】根据中心投影的特点可知，当乒乓球越接近灯泡时，离光源越近，影子越大，即可求解．【详解】解：根据中心投影的特点可知，当乒乓球越接近灯泡时，离光源越近，影子越大，故答案为：越大．【点睛】此题考查了中心投影的特点，等长的物体平行于地面放置时，离点光源越近，影子越长；离点光源越远，影子越短，熟练掌握中心投影的性质是解题的关键．16．（2021·北京·九年级专题练习）一块直角三角形板，，，，测得边的中心投影长为，则长为__．【答案】【分析】由题意易得△ABC∽△，根据相似比求解即可．【详解】解：，，，＝24，∴，∵△，，即，故答案为：．【点睛】本题综合考查了中心投影的特点和规律以及相似三角形性质的运用，解题的关键是利用中心投影的特点可知这两组三角形相似，利用其相似比作为相等关系求出所需要的线段．17．（2021·陕西·榆林市第一中学分校七年级月考）如图所示是从不同的方向观察一个圆柱体得到的形状图，由图中数据计算此圆柱体的侧面积为________（结果保留）．            从正面看          从左面看        从上面看【答案】【分析】根据主视图确定出圆柱体的底面直径与高，然后根据圆柱体的侧面积公式列式计算即可得解．【详解】解：由图可知，圆柱体的底面直径为2，高为3，所以，侧面积．故答案为：．【点睛】本题考查了立体图形的三视图和学生的空间想象能力，圆柱体的侧面积公式，解题的关键是根据主视图判断出圆柱体的底面直径与高．18．（2021·辽宁·沈阳市第七中学七年级月考）一个由若干个相同的小正方体组成的几何体的主视图和俯视图如图所示，则小正方体的最少个数为___．【答案】7【分析】易得这个几何体共有3层，由俯视图可得第一层正方体的个数，由主视图可得第二层和第三层正方体的可能的最少个数，相加即可．【详解】解：由俯视图易得最底层有4个正方体，由主视图第二层最少有2个正方体，由主视图第三层最少有1个正方体，那么最少有4＋2＋1＝7个立方体．故答案是：7．【点睛】本题考查了由三视图判断几何体．俯视图小正方形的个数即为最底层的小正方体的个数，主视图第二层和第三层小正方形的个数即为其余层数小正方体的最少个数．三、解答题（本题共8道题，19-21每题6分，22-25每题8分，26题10分，满分60分）19．（2021·全国·九年级课时练习）把图中的几何体与它们对应的三视图用线连接起来．【答案】见解析【分析】直接利用简单几何体的三视图进而分析得出答案．【详解】解：如图所示：．【点睛】本题主要考查了简单几何体的三视图，正确掌握观察角度是解题关键．20．（2021·山东芝罘·八年级期末）在同一时刻两根垂直于水平地面的木竿在太阳光下的影子如图所示，其中木竿AB=2.5m，它的影子BC=2m，木竿PQ的影子有一部分落在了墙上（MN），PM=1.6m，MN=1m，求木竿PQ的长度．【答案】木杆PQ的长度为3m．【分析】过N点作ND⊥PQ于D，先根据同一时刻物高与影长成正比求出QD的影长，再根据此影长列出比例式即可．【详解】解：过N点作ND⊥PQ于D，如图所示：∴，又∵AB=2.5，BC=2，DN=PM=1.6，NM=1，∴QD===2（m），∴PQ=QD+DP=QD+NM=2+1=3（m）．答：木杆PQ的长度为3m．【点睛】本题考查了平行投影；在运用投影的知识解决实际问题时，要能够从实际问题中抽象出简单的数学模型是解决问题的关键．21．（2021·江苏·姜堰区实验初中九年级月考）如图，AB和DE是直立在地面上的两根立柱．AB＝4m，某一时刻AB在阳光下的投影BC＝3m．（1）请你在图中画出此时DE在阳光下的投影．（2）在测量AB的投影时，同时测量出DE在阳光下的投影长为8m，请你计算DE的长．【答案】（1）画图见解析，（2） m，【分析】（1）连接AC，过点D作DF∥AC，即可画出投影；（2）根据在同一时刻，不同物体的物高和影长成比例；构造比例关系AB：DE＝BC：EF．计算可得DE的值．【详解】解：（1）连接AC，过点D作DF∥AC，交直线BC于点F，线段EF即为DE的投影． （2）∵AC∥DF，∴∠ACB＝∠DFE．∵∠ABC＝∠DEF＝90°∴△ABC∽△DEF．∴AB：DE＝BC：EF，∵AB＝4m，BC＝3m，EF＝8m，∴4：3＝DE：8∴DE＝（m）．【点睛】本题考查了平行投影，在同一时刻，不同物体的物高和影长成比例．解题关键是明确投影的知识并结合相似画图与计算．22．（2021·陕西陈仓·七年级期中）一个几何体由几个大小相同的小立方块搭成，从上面看到的这个几何体的形状图如图所示，其中小正方形中的数字表示在该位置的小立方块的个数．请画出从正面和左面看到的这个几何体的形状图．【答案】答案见解析【分析】根据题目条件可知，该几何体从正面看有3列，各列中小正方形的数目分别为2，2和3；从左面看有2列，各列中小正方形的数目分别为3和2；据此可画出图形．【详解】解：从正面看到的该几何体的形状图如下图所示：从左面看到的该几何体的形状图如下图所示：【点睛】本题考查几何体的三视图画法，由几何体的俯视图及小正方形内的数字，可知主视图的列数与俯视数的列数相同，且每列小正方形数目为俯视图中该列小正方形数字中的最大数字；左视图的列数与俯视图的行数相同，且每列小正方形数目为俯视图中相应行中小正方形数字中的最大数字．23．（2020·福建·漳州三中七年级期中）如图，是某几何体从三个方向分别看到的图形．（1）写出这个几何体的名称       ．（2）若图①的长为，宽为；图②的宽为；图③直角三角形的斜边长为，求这个几何体的所有棱长的和是多少？【答案】（1）三棱柱；（2）【分析】（1）直接利用三视图可得出几何体的形状；（2）利用已知即可求出棱长之和．【详解】解：（1）∵从正面看和从左面看都是长方形，从上面看是三角形，∴这个几何体是三棱柱；（2）由题意可得：棱长和为；【点睛】此题主要考查了由三视图判断几何体的形状以及几何体的展开图等知识，正确得出物体的形状是解题关键．24．（2021·河北宽城·九年级期末）如图，在阳光下，小玲同学测得一根长为1米的垂直地面的竹竿的影长为0.6米，同时小强同学在测量树的高度时，发现树的影子有一部分（0.2 米）落在教学楼的第一级台阶上，落在地面上的影长为4.42米，每级台阶高为0.3米．小玲说：“要是没有台阶遮挡的话，树的影子长度应该是 4.62米．”小强说：“要是没有台阶遮挡的话，树的影子长度肯定比 4.62米要长．”（1）你认为谁的说法对?并说明理由；（2）请根据小玲和小强的测量数据计算树的高度．【答案】（1）小强的说法对，理由见解析；（2）8米．【分析】（1）画出解题示意图，利用同一时刻，物高与影长成正比，计算判断即可；（2）利用同一时刻，物高与影长成正比，计算判断即可；【详解】解：（1）小强的说法对；根据题意画出图形，如图所示，根据题意，得，∵DE=0．3米，∴（米）．∵GD∥FH，FG∥DH，∴四边形DGFH是平行四边形，∴米．∵AE=4．42米，∴AF=AE+EH+FH=4．42+0．18+0．2=4．8（米），即要是没有台阶遮挡的话，树的影子长度是4．8米，∴小强的说法对；（2）由（1）可知：AF=4．8米．∵，∴米．答：树的高度为8米．【点睛】本题考查了太阳光下的平行投影问题，准确理解影长的意义，灵活运用同一时刻，物高与影长成正比是解题的关键．25．（2021·辽宁抚顺·三模）某工厂要加工一批上下底密封纸盒，设计者给出了密封纸盒的三视图，如图1．（1）由三视图可知，密封纸盒的形状是__________；（2）根据该几何体的三视图，在图2中补全它的表面展开图；（3）请你根据图1中数据，计算这个密封纸盒的表面积．（结果保留根号）【答案】（1）（正）六棱柱；（2）见解析；（3）【分析】（1）通过三视图，发挥想象力可以得到答案；
（2）由（1）得到的答案可以得到表面展开图；
（3）分别计算出侧面积和上下底面积即可得到答案 ．　　【详解】解：（1）根据该几何体的三视图知道它是一个（正）六棱柱；（2）由（1）可以得到六棱柱的表面展开图如图：（3）由图中数据可知：六棱柱的高为12，底面边长为5，∴六棱柱的侧面积为．又∵密封纸盒的底面面积为：，∴六棱柱的表面积为：．【点睛】本题考查三视图与展开图的综合应用，充分发挥想象力是解题关键．26．（2021·全国·九年级）用小立方块搭一个几何体，使它从正面和上面看到的形状如图所示，从上面看到形状中小正方形中的字母表示在该位置上小立方块的个数，请问：（1）b＝　　；c＝　　；（2）这个几何体最少由　　个小立方块搭成，最多由　　个小立方块搭成；（3）从左面看这个几何体的形状图共有　　种，请在所给网格图中画出其中的任意一种．【答案】（1）1，3；（2）9，11；（3）4，左视图见解析．【分析】（1）由主视图可知，第二列小立方体的个数均为1，那么b＝1；第二列小立方体的个数均为1，那么c＝3；（2）第一列小立方体的个数最少为2+1+1，最多为2+2+2，那么加上其它2列小立方体的个数即可；（3）由（2）可知，这个几何体最少由9个小立方块搭成，最多由11个小立方块搭成，所以共有7种情况；其中从左面看该几何体的形状图共有4种；小立方块最多时几何体的左视图有3列，每列小正方形数目分别为3，2，2．【详解】（1）b＝1，c＝3；（2）这个几何体最少由4+2+3＝9个小立方块搭成；这个几何体最多由6+2+3＝11个小立方块搭成；（3）能搭出满足条件的几何体共有7种情况，其中从左面看该几何体的形状图共有4种；小立方块最多时几何体的左视图如图所示：故答案为：（1）1，3；（2）9，11；（3）4．【点评】本题考查了三视图的知识，主视图是从物体的正面看得到的视图，左视图是从物体的左面看得到的视图；注意主视图主要告知组成的几何体的层数和列数．