5.1.1相交线（同步练习）人教版七年级数学下册

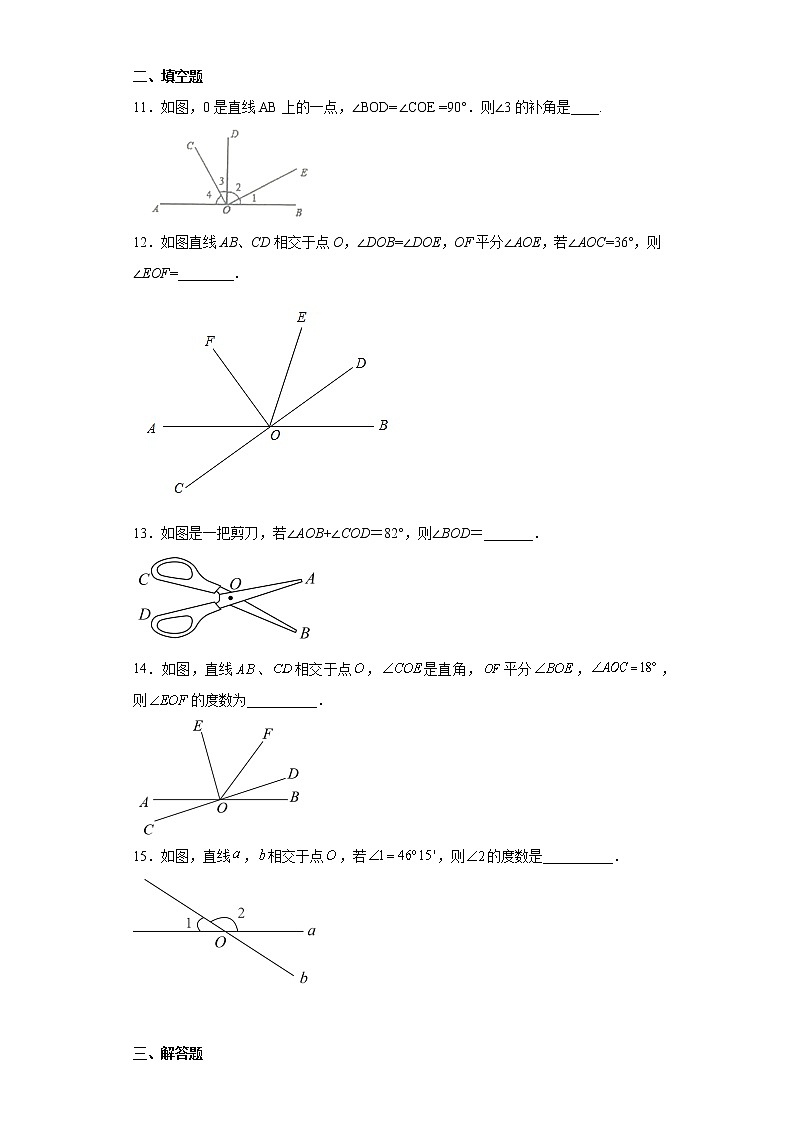
5.1.1相交线（同步练习）一、单选题1．如图，已知直线AB、CD相交于O，如果∠AOC＝2x°，∠BOD＝(7x－100)°，则∠AOD的度数为(　　)A．100°B．120°C．130°D．140°2．如图，直线AB、CD相交于点O，OE 平分∠BOD，若∠AOE=150°，则∠AOC的度数为(  )A．50° B．60° C．70° D．80°3．如图，直线和交于点，平分，若，则的度数为（    ）A．75° B．80° C．100° D．120°4．如图1，其中∠1与∠2是同位角的是（  ）A．②③ B．②③④ C．①②④ D．③④5．如图，直线、交于点O，平分，若，则等于（    ）．A． B． C． D．6．如图，直线a，b相交于点O，∠1＝110°，则∠2的度数是（　　）A．70° B．90° C．110° D．130°7．判断下列图中和是对顶角的是（ ）A． B． C． D．8．如图，若,相交于点，过点作，则下列结论不正确的是A．与互为余角 B．与互为余角C．与互为补角 D．与是对顶角9．若三条直线交于一点，则共有对顶角(平角除外) （  ）A．6对 B．5对 C．4对 D．3对10．下面四个图中，∠1=∠2一定成立的是（     ）A． B． C． D． 二、填空题11．如图，0是直线AB上的一点，∠BOD=∠COE =90°．则∠3的补角是____.12．如图直线AB、CD相交于点O，∠DOB=∠DOE，OF平分∠AOE，若∠AOC=36°，则∠EOF=________．13．如图是一把剪刀，若∠AOB+∠COD＝82°，则∠BOD＝_______．14．如图，直线、相交于点，是直角，平分，，则的度数为__________．15．如图，直线，相交于点，若，则的度数是__________． 三、解答题16．为了探究n条直线能把平面最多分成几部分,我们从最简单的情形入手:①一条直线把平面分成2部分;②两条直线可把平面最多分成4部分;③三条直线可把平面最多分成7部分;④四条直线可把平面最多分成11部分;……把上述探究的结果进行整理,列表分析:直线条数把平面最多分成的部分数写成和的形式121+1241+1+2371+1+2+34111+1+2+3+4……… (1)当直线条数为5时,把平面最多分成____部分,写成和的形式:______; (2)当直线条数为10时,把平面最多分成____部分; (3)当直线条数为n时,把平面最多分成多少部分?17．如图，直线AB、CD相交于点O，OE⊥AB，OF⊥CD．（1）写出图中∠AOF的余角　   　；（2）如果∠EOF=∠AOD，求∠EOF的度数．18．已知：如图，直线AB、CD相交于点O，OE⊥OC，OF平分∠AOE.（1）若，则∠AOF的度数为______；（2）若，求∠BOC的度数．19．如图，直线 AB，CD 相交于点 O，EO  AB 于 O，∠COE=55°，则∠BOD的度数是多少？20．如图,直线相交于点．（1）的对顶角是_______．图中共有对顶角         对．（2）若, , 求的度数．21．已知：如图，平面上有A、B、C、D四个点，根据下列语句画出图形(1)画射线AC；(2)连接AB、BC、BD，线段BD与射线AC交于点O；(3)①在线段AC上作一条线段CF，使得CF＝AC－BD；②观察图形，我们发现线段AB＋BC＞AC，得出这个结论的依据是什么？③∠AOB与∠DOC相等吗？说明理由．
参考答案：1．D2．B3．A4．C5．C6．C7．D8．D9．A10．D11．∠AOE；12．54°13．139°14．15．16．(1) 16； (2) 56； (3)部分17．（1）∠AOC、∠FOE、∠BOD．（2）30°．18．（1）（2）19．35°20．(1) ∠AOF，6；（2）160°．21．（1）如图，射线即为所求； （2）解：如图，线段AB、BC、BD即为所求；（3）①如图，以A为圆心，以BD为半径画弧交AC于点F，FC即为所求；②两点之间，线段最短；③相等，理由如下：∵∠AOB＋∠AOD＝180°，∠DOC＋∠AOD＝180°∴∠AOB＝∠DOC．