高中数学高考专题13 利用导数证明或求函数的单调区间(原卷版)

这是一份高中数学高考专题13 利用导数证明或求函数的单调区间(原卷版)，共8页。试卷主要包含了多选题，单选题，解答题等内容，欢迎下载使用。
1．已知函数，数列的前n项和为，且满足，，则下列有关数列的叙述正确的是（ ）
A．B．C．D．
2．设函数的导函数为，则（ ）
A．B．是的极值点
C．存在零点D．在单调递增
3．已知函数，，则下列结论正确的有（ ）
A．在区间上单调递减
B．若，则
C．在区间上的值域为
D．若函数，且，在上单调递减
4．已知函数，给出下列四个结论，其中正确的是（ ）
A．曲线在处的切线方程为
B．恰有2个零点
C．既有最大值，又有最小值
D．若且，则
5．已知函数，则下列说法正确的是（ ）
A．当时，在单调递增
B．当时，在处的切线为轴
C．当时，在存在唯一极小值点，且
D．对任意，在一定存在零点
二、单选题
6．已知定义域为R的函数的图象连续不断，且，，当时，，若，则实数m的取值范围为（ ）
A．B．C．D．
7．函数的图象大致是（ ）
A．B．C．D．
8．设函数在上存在导数，对于任意的实数，有，当时，，若，则实数的取值范围是（ ）
A．B．C．D．
9．函数，若，，，则（ ）
A．B．C．D．
10．已知函数，则其单调增区间是（ ）
A．B．C．D．
11．某数学兴趣小组对形如的某三次函数的性质进行研究，得出如下四个结论，其中有且只有一个是错误的，则错误的结论一定是（ ）
A．函数的图象过点(2，1)
B．函数在x＝0处有极值
C．函数的单调递减区间为[0，2]
D．函数的图象关于点(1，0)对称
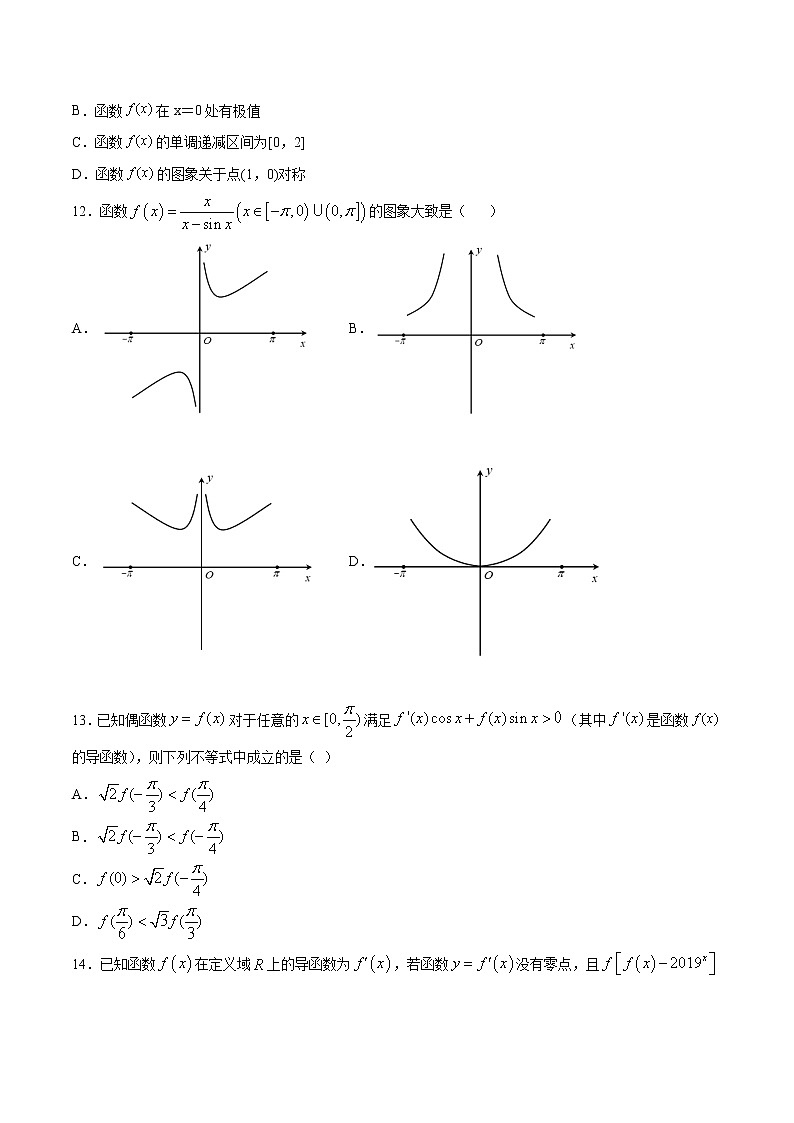
12．函数的图象大致是（ ）
A．B．
C．D．
13．已知偶函数对于任意的满足（其中是函数的导函数），则下列不等式中成立的是（ ）
A．
B．
C．
D．
14．已知函数在定义域上的导函数为，若函数没有零点，且，当在上与在上的单调性相同时，则实数k的取值范围是（ ）
A．B．C．D．
15．函数y=f(x)的导函数y=f′(x)的图象如图所示，给出下列命题：
①-3是函数y=f(x)的极值点；
②y=f(x)在区间(-3，1)上单调递增；
③-1是函数y=f(x)的最小值点；
④y=f(x)在x=0处切线的斜率小于零.
以上正确命题的序号是（ ）
A．①②B．③④C．①③D．②④
16．已知f（x）是定义在R上的偶函数，且f（2）＝1，当x＞0时，xf′（x）+f（x）＞1，则不等式的解集为（ ）
A．(-∞，2)∪(2，+∞)B．(-∞，2)∪(0，2)
C．(-2，0)∪(2，+∞)D．(-2，0)∪(0，2)
17．已知函数，，若对任意，总存在，使得成立，则实数的取值范围为（ ）
A．B．
C．D．
18．若定义在上的函数满足，且当时，，则满足的值（ ）
A．恒小于0B．恒等于0C．恒大于0D．无法判断
19．下列区间是函数的单调递减区间的是（ ）
A．B．C．D．
20．已知为偶函数，且，令，若时，，关于的不等式的解集为（ ）
A．或B．
C．D．或
21．已知，则函数的单调减区间为（ ）
A．B．C．D．
22．若函数在上是单调函数，则实数的取值范围是（ ）
A．B．C．D．
23．已知f(x)是定义在R上的连续函数，f′(x)是f(x)的导函数，且f(x)-f(-x)+4x=0.若当x>0时，f′(x)>-2，则不等式f(x-2)-f(x)>4的解集为（ ）
A．(-∞，-1)B．(-∞，1)C．(-1，+∞)D．(1，+∞)
24．已知函数，若，，，则（ ）
A．B．C．D．
三、解答题
25．函数.
（1）当时，求的单调区间；
（2）当时，恒成立，求整数的最大值.
26．函数.
（1）当时，求的单调区间；
（2）当，时，证明：.
27．函数.
（1）若，求的单调性；
（2）当时，若函数有两个零点，求证：.
28．设为实数，已知函数.
（1）当时，求的单调区间；
（2）当时，若有两个不同的零点，求的取值范围.
29．已知函数.
（1）若a= -2，求函数f(x)的单调区间；
（2）若函数f(x)有两个极值点x1，x2，求证.
30．设函数.
（1）若，求的单调区间；
（2）若时，求的取值范围.
31．已知函数.
（1）求函数的单调区间；
（2）在平面直角坐标系中，直线与曲线交于，两点，设点的横坐标为，的面积为.
（i）求证：；
（ii）当取得最小值时，求的值.
32．已知函数.
（1）求在点处的切线方程；
（2）求的单调区间；
（3）若的定义域为时，值域为，求的最大值.
33．如图，点为某沿海城市的高速公路出入口，直线为海岸线，，，是以为圆心，半径为的圆弧型小路.该市拟修建一条从通往海岸的观光专线，其中为上异于的一点，与平行，设.
（1）证明：观光专线的总长度随的增大而减小；
（2）已知新建道路的单位成本是翻新道路的单位成本的倍.当取何值时，观光专线的修建总成本最低？请说明理由.
34．已知函数是自然对数的底数，是的导函数．
（1）若，求证：在单调递增；
（2）证明：有唯一的极小值点（记为），且．
35．已知函数，，，且.
（1）若函数在处取得极值，求函数的解析式；
（2）在（1）的条件下，求函数的单调区间；
（3）设，为的导函数.若存在，使成立，求的取值范围.