高中数学高考专题16 平面向量数量积及其应用（教师版）

这是一份高中数学高考专题16 平面向量数量积及其应用（教师版），共40页。试卷主要包含了已知向量，满足，，则，已知向量 ， 则ABC=，已知向量，，，则，设四边形为平行四边形，，等内容，欢迎下载使用。


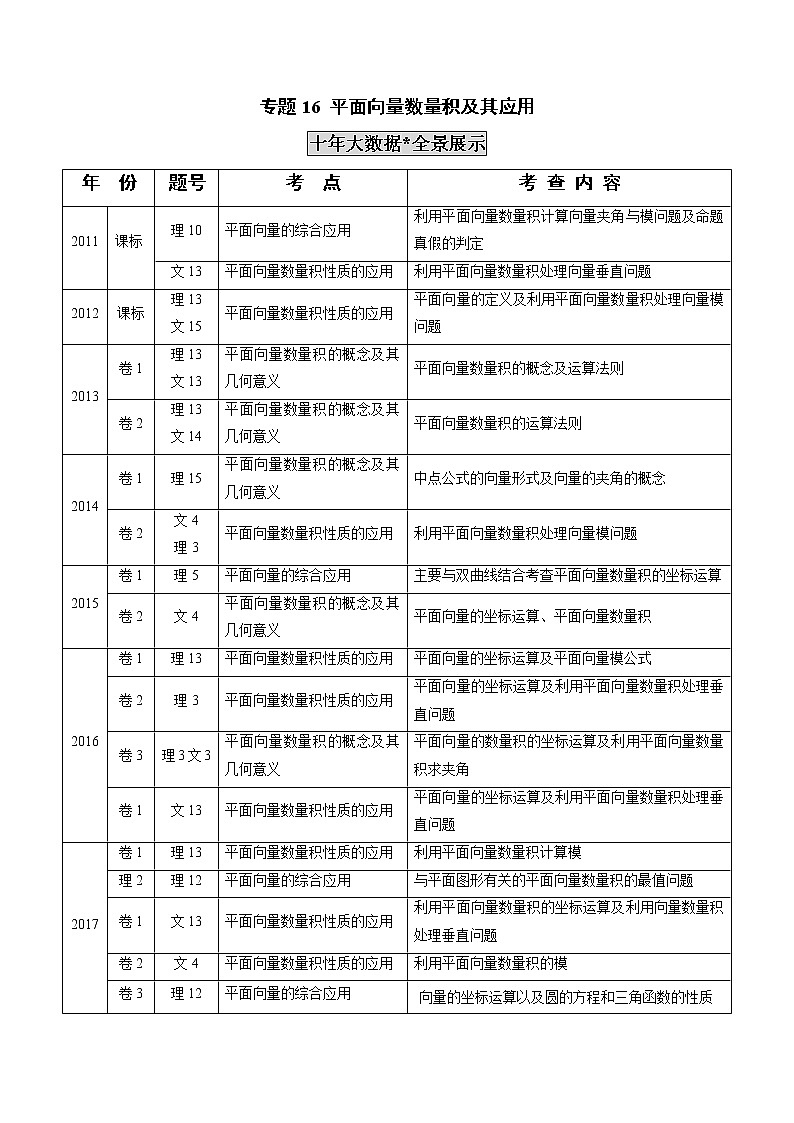
大数据分析*预测高考
十年试题分类*探求规律
考点51平面向量数量积的概念、其几何意义及其运算律
1．（2020全国Ⅲ理6）已知向量满足，则（ ）
A． B． C． D．
【答案】D
【思路导引】计算出、的值，利用平面向量数量积可计算出的值．
【解析】，，，．
，因此．故选D．
2．（2020山东7）已知是边长为的正六边形内的一点，则的取值范围是（ ）
A． B． C． D．
【答案】A
【思路导引】首先根据题中所给的条件，结合正六边形的特征，得到在方向上的投影的取值范围是，利用向量数量积的定义式，求得结果．
【解析】解法一：的模为2，根据正六边形的特征，可以得到在方向上的投影的取值范围是，结合向量数量积的定义式，可知等于的模与在方向上的投影的乘积，所以的取值范围是，故选：A．
解法二：如图，建立平面直角坐标系，由题意知，，，，设，则，∵，∴，∴的取值范围是．
3．（2018•新课标Ⅱ，理4）已知向量，满足，，则
A．4B．3C．2D．0
【答案】B
【解析】向量，满足，，则，故选．
4．（2016新课标，理3）已知向量 ， 则ABC=
(A)300 (B) 450 (C) 600 (D)1200
【答案】A
【解析】由题意，得，所以，故选A．
5．（2017北京）设， 为非零向量，则“存在负数，使得”是“”的
A．充分而不必要条件 B．必要而不充分条件
C．充分必要条件 D．既不充分也不必要条件
【答案】A
【解析】因为为非零向量，所以的充要条件是．因为，则由可知的方向相反，，所以，所以“存在负数，使得”可推出“”；而可推出，但不一定推出的方向相反，从而不一定推得“存在负数，使得”，所以“存在负数，使得”是“”的充分而不必要条件．
6．（2013湖北）已知点、、、，则向量在方向上的投影为
A． B． C． D．
【答案】A
【解析】=（2，1），=（5，5），则向量在向量方向上的射影为
7．（2011辽宁）已知向量，，，则
A． B． C．6 D．12
【答案】D
【解析】 ∵，由，得，∴，解得．
8．(2015山东)已知菱形ABCD 的边长为，，则＝
A． B． C． D．
【答案】D
【解析】由菱形的边长为，可知，
．
9．（2015四川）设四边形为平行四边形，，．若点满足
，，则（ ）
A．20 B．15 C．9 D．6
【答案】C
【解析】，所以 ====9，选C．
10．（2014天津）已知菱形的边长为2，，点分别在边上，，．若，，则
A． B． C． D．
【答案】C
【解析】 因为，所以，因为，所以，，因为，所以，即 ①，同理可得 ②，①+②得．
11．（2012天津）在△ABC中，A=90°，AB=1，设点P，Q满足，，．若，则（ ）
A． B． C． D．2
【答案】B
【解析】如图，设 ，则，又 = =，，∴= ==，即，选B．
12．（2020全国Ⅰ文14）设向量，若，则 ．
【答案】5
【思路导引】根据向量垂直，结合题中所给的向量的坐标，利用向量垂直的坐标表示，求得结果．
【解析】由可得，又∵，
∴，即，故答案为：．
13．（2020全国Ⅱ理13）已知单位向量的夹角为45°，与垂直，则__________．
【答案】
【思路导引】首先求得向量的数量积，然后结合向量垂直的充分必要条件即可求得实数k的值．
【解析】由题意可得：，由向量垂直的充分必要条件可得：，
即：，解得：，故答案为：．
14．（2020全国Ⅰ理14）设为单位向量，且，则 ．
【答案】
【思路导引】整理已知可得：，再利用为单位向量即可求得，对变形可得：，问题得解．
【解析】∵为单位向量，∴，
∴，解得：，
∴，故答案为：．
15．（2019•新课标Ⅲ，文13）已知向量，，则， ．
【答案】
【解析】由题知，，，，
，．
16．（2014新课标Ⅰ，理15）已知A，B，C是圆O上的三点，若，则与的夹角为 ．
【答案】
【解析】∵，∴O为线段BC中点，故BC为的直径，
∴，∴与的夹角为．
17．（2013新课标Ⅰ，理13文13）已知两个单位向量a，b的夹角为60°，c＝ta＋(1－t)b，若b·c=0，则t=_____．
【答案】2
【解析】=====0，解得=．
18．（2013新课标Ⅱ，理13文14）已知正方形ABC的边长为2，E为CD的中点，则= ．
【答案】2
【解析】===4-2=2．
19．（2011江苏）已知，是夹角为的两个单位向量，，， 若，则的值为 ．
【答案】
【解析】由题意知，即，即，化简可求得．
20．（2017天津）在中，，，．若，
，且，则的值为___________．
【答案】
【解析】，，则 ==，解得．
21．（2014天津）已知菱形的边长为，，点，分别在边、上，，．若，则的值为________．
【答案】
【解析】因为，菱形的边长为2，所以．因为，由，所以，解得．
考点52平面向量数量积性质的应用
1．（2020全国Ⅱ文5）已知单位向量的夹角为60°，则在下列向量中，与垂直的是（ ）
A．B．C．D．
【答案】D
【思路导引】根据平面向量数量积的定义、运算性质，结合两平面向量垂直数量积为零这一性质逐一判断即可．
【解析】由已知可得：．
A：∵，∴本选项不符合题意；
B：∵，∴本选项不符合题意；
C：∵，∴本选项不符合题意；
D：∵，∴本选项符合题意．故选D．
2．（2019•新课标Ⅰ，理7文8）已知非零向量，满足，且，则与的夹角为（ ）
A．B．C．D．
【答案】B
【解析】，，，，，故选．
3．（2017•新课标Ⅱ，文4）设非零向量，满足则
A．B．C．D．
【答案】A
【解析】非零向量，满足，，即，∴，，故选．
4．（2016新课标，理3）已知向量，且，则m=（ ）
（A）－8 （B）－6 （C）6 （D）8
【答案】D
【解析】由题知a+b=，所以==0，解得，故选D．
5．（2014新课标Ⅱ，理3文4）设向量满足，，则（ ）
A．1 B． 2 C． 3 D． 5
【答案】A
【解析】∵，，∴……①，……②．
由①②得：，故选A．
6．(2018北京)设，均为单位向量，则“”是“⊥”的
A．充分而不必要条件B．必要而不充分条件
C．充分必要条件D．既不充分也不必要条件
【答案】C
【解析】∵，∴，∴
，又，∴，∴；反之也成立，故选C．
7．（2016年山东）已知非零向量满足，．若，则实数t的值为（ ）
A．4 B．–4 C． D．–
【答案】B
【解析】由可得，即，所以．故选B．
8．(2015重庆)若非零向量，满足，且，则与的夹角为（ ）
A． B． C． D．
【答案】A
【解析】由题意，即，所以，，，选A．
9．（2015陕西）对任意向量，下列关系式中不恒成立的是
A． B．
C． D．
【答案】B
【解析】对于A选项，设向量、的夹角为，∵，∴A选项正确；对于B选项，∵当向量、反向时，，∴B选项错误；对于C选项，由向量的平方等于向量模的平方可知，C选项正确；对于D选项，根据向量的运算法则，可推导出，故D选项正确，综上选B．
10．（2015安徽）是边长为的等边三角形，已知向量，满足，，则下列结论正确的是 （ ）
A． B． C． D．
【答案】D
【解析】如图由题意，，故，故错误；，所以，又，所以，故错误；设中点为，则，且，所以，故选D．
11．(2014山东)已知向量． 若向量的夹角为，则实数（ ）
A． B． C．0 D．
【答案】B
【解析】由题意得，两边平方化简得，
解得，经检验符合题意．
12．（2014重庆）已知向量，，，且，则实数
A． B． C． D．
【答案】C
【解析】∵，，所以=．解得，选C
13．（2012陕西）设向量=（1，）与=（1，2）垂直，则等于
A． B． C．0 D．－1
【答案】C
【解析】正确的是C．
14．（2012浙江）设，是两个非零向量
A．若，则
B．若，则
C．若，则存在实数，使得
D．若存在实数，使得，则
【答案】C
【解析】 因为，，所以不垂直，A不正确，同理B也不正确；因为，则，所以共线，故存在实数，使得，C正确；若，则，此时，所以D不正确．
15．（2019•新课标Ⅲ，理13）已知，为单位向量，且，若，则， ．
【答案】
【解析】∵，，
，，．
16．（2017•新课标Ⅰ，理13）已知向量，的夹角为，，，则 ．
【答案】
【解析】向量，的夹角为，且，，
，．
17．（2017•新课标Ⅰ，文13）已知向量，，若向量与垂直，则 ．
【答案】7
【解析】向量，，，向量与垂直，
，解得．
18．（2017•新课标Ⅲ，文13）已知向量，，且，则 ．
【答案】2
【解析】向量，，且，，解得．
19．(2016新课标，理13)设向量a=(m，1)，b=(1，2)，且|a+b|2=|a|2+|b|2，则m= ．
【答案】-2
【解析】由|a+b|2=|a|2+|b|2得，=0，所以，解得．
20．（2016•新课标Ⅰ，文13）设向量，，且，则 ．
【答案】
【解析】，，即，∴．
21．（2012课标，理13）已知向量，夹角为，且||=1，||=，则||= ．
【答案】．
【解析】∵||=，平方得，即，解得||=或（舍）
22．（2011新课标，文13）已知与为两个不共线的单位向量，为实数，若向量与向量垂直， 则= ．
【答案】1
【解析】∵与为 两个不共线的单位向量，∴||=1，||=1，且与夹角不为0也不为，∴，又∵向量与向量垂直，∴====0，∴=0，∴=1．
23．(2017山东)已知，是互相垂直的单位向量，若与的夹角为，则实数的值是 ．
【答案】
【解析】，
，
，
，解得：．
24．（2015湖北）已知向量，，则 ．
【答案】9
【解析】因为，，所以 ．
25．（2014四川）平面向量，，（），且与的夹角等于与的夹角，则____________．
【答案】2
【解析1】，因为，，所以，又，所以，即
26．（2013北京）已知向量，夹角为，且，，则．
【答案】
【解析】
27．（2012湖北）已知向量=（1，0），=（1，1），则
（Ⅰ）与同向的单位向量的坐标表示为____________；
（Ⅱ）向量与向量夹角的余弦值为____________．
【答案】（Ⅰ） （Ⅱ）
【解析】（Ⅰ）由，得．设与同向的单位向量为，则且，解得故．即与同向的单位向量的坐标为．
（Ⅱ）由，得．设向量与向量的夹角为，则．
28．（2012安徽）若平面向量，满足：；则的最小值是．
【答案】
【解析】，
∴
29．（2011安徽）已知向量满足，且，，则与的夹角为 ．
【答案】
【解析】设与的夹角为，由题意有，所以，因此，所以．
考点53平面向量的综合应用
1．（2019•新课标Ⅱ，理3）已知，，，则
A．B．C．2D．3
【答案】C
【解析】，，，，即，则，故选．
2．（2017•新课标Ⅱ，理12）已知是边长为2的等边三角形，为平面内一点，则的最小值是
A．B．C．D．
【答案】B
【解析】建立如图所示的坐标系，以中点为坐标原点，则，，，
设，则，，，则，当，时，取得最小值，故选．
3．（2017•新课标Ⅲ，理12）在矩形中，，，动点在以点为圆心且与相切的圆上．若，则的最大值为
A．3B．C．D．2
【答案】A
【解析】如图：以为原点，以，所在的直线为，轴建立如图所示的坐标系，
则，，，，动点在以点为圆心且与相切的圆上，
设圆的半径为，，，，，，
圆的方程为，设点的坐标为，，
，，，，，，
，，，其中，∵，∴，故的最大值为3，故选．
4．（2015新课标Ⅰ，理5）已知M（x0，y0）是双曲线C：上的一点，F1、F2是C上的两个焦点，若＜0，则y0的取值范围是（ ）
（A）（-，）（B）（-，）
（C）（，） （D）（，）
【答案】A
【解析】由题知，，所以= =，解得，故选A．
5．（2011新课标，理10）已知与均为单位向量，其中夹角为，有下列四个命题
：∈[0，） ：∈(，]
： ∈[0， ） ：∈(，]
其中真命题是
（A）， (B) ， (C) ， (D) ，
【答案】A
【解析】由得，，即＞，即=＞，
∵∈[0，]，∴∈[0，），
由得，，即＜，即=＜，∵∈[0，]，∴∈(，]，故选A．
6．（2016年天津）已知是边长为1的等边三角形，点分别是边的中点，连接并延长到点，使得，则的值为
A． B． C． D．
【答案】B
【解析】设，，∴，，，
∴，故选B．
7．（2014安徽）设为非零向量，，两组向量和均由2个和2个排列而成，若所有可能取值中的最小值为，则与的夹角为
A． B． C． D．0
【答案】B
【解析】设，若的表达式中有0个，则，记为，若的表达式中有2个，则，记为，若的表达式中有4个，则，记为，又，所以，，
，∴，故，设的夹角为，
则，即，又，所以．
8．（2014浙江）设为两个非零向量，的夹角，已知对任意实数，是最小值为1
A．若确定，则唯一确定 B．若确定，则唯一确定
C．若确定，则唯一确定 D．若确定，则唯一确定
【答案】B
【解析】由于，令，而是任意实数，所以可得的最小值为，
即，则知若确定，则唯一确定．
9．（2013福建）在四边形中，，则该四边形的面积为
A． B． C．5 D．10
【答案】C
【解析】 因为，所以，所以四边形的面积为，故选C．
10．（2013浙江）设，是边上一定点，满足，且对于边上任一点，恒有．则
A． B． C． D．
【答案】D
【解析】由题意，设，则，过点作的垂线，垂足为，
在上任取一点，设，则由数量积的几何意义可得，
，，
于是恒成立，相当于恒成立，
整理得恒成立，只需
即可，于是，因此我们得到，即是的中点，故△是等腰三角形，所以．
11．（2013湖南）已知是单位向量，．若向量满足，则的最大值为
A． B． C． D．
【答案】C
【解析】建立平面直角坐标系，令向量的坐标，又设，代入得，又的最大值为圆上的动点到原点的距离的最大值，即圆心(1，1)到原点的距离加圆的半径，即．
12．（2013重庆）在平面上，，，．若，则的取值范围是
A． B． C． D．
【答案】D
【解析】因为⊥，所以可以A为原点，分别以，所在直线为x轴，y轴建立平面直角坐标系．设B1(a，0)，B2(0，b)，O(x，y)，则＝＋＝(a，b)，即P(a，b)．由||＝||＝1，得(x－a)2＋y2＝x2＋(y－b)2＝1，所以(x－a)2＝1－y2≥0，(y－b)2＝1－x2≥0，由||＜，得(x－a)2＋(y－b)2＜，即0≤1－x2＋1－y2＜，所以＜x2＋y2≤2，即，所以||的取值范围是，故选D．
13．(2018天津)如图，在平面四边形中，，，，
． 若点为边上的动点，则的最小值为
A． B． C． D．
【答案】A
【解析】以为坐标原点，所在直线为轴，建立如图的平面直角坐标系，因为在平面四边形中，，，所以，，，设，，所以，，因为，所以，即，解得，即，因为在上，所以，由，得，即，因为，，所以 ==，令，，因为函数在 上单调递减，在上单调递增，所以．所以的最小值为，故选A．
14．(2018浙江)已知，，是平面向量，是单位向量．若非零向量与的夹角为，向量满足，则的最小值是（ ）
A． B．C．2 D．
【答案】A
【解析】解法一 设为坐标原点，，，，由得，即，所以点的轨迹是以为圆心，l为半径的圆．因为与的夹角为，所以不妨令点在射线()上，如图，数形结合可知．故选A．
解法二 由得．设，，，所以，，所以，取的中点为．则在以为圆心，为直径的圆上，如图，设，作射线，使得，所以 =．故选A．
15．（2017浙江）如图，已知平面四边形，，，，与交于点，记，，，则
A．<【答案】C
【解析】如图所示，四边形是正方形，为正方形的对角线的交点，易得，而，∴与为钝角，与为锐角．根据题意，∴，同理．做于，又．∴，而，∴，而，
∴，即，∴，选C．
16．（2016四川）在平面内，定点A，B，C，D满足 ==，=
==2，动点P，M满足=1，=，则的最大值是
A． B． C． D．
【答案】B
【解析】由知，为的外心．由=
= 知为的内心，所以为正三角形，易知其边长为，取的中点，因为是的中点，所以，所以，则．故选B．
17．（2015福建）已知， ， ，若点是所在平面内一点，且 ，则 的最大值等于（ ）
A．13 B．15 C．19 D．21
【答案】A
【解析】以题意，以点为坐标原点，以所在的直线为轴，所在的直线为 轴建立如图所示的平面直角坐标系，所以点，，，所以== 13（当且仅当，即时取等号），所以的最大值为13．故选A．
18．（2015湖南）已知点在圆上运动，且．若点的坐标为，则的最大值为（ ）
A．6 B．7 C．8 D．9
【答案】B
【解析】由题意得，AC为圆的直径，故可设，，，∴，而，∴的最大值为，故选B．
19．（2014安徽）在平面直角坐标系中，已知向量，，，点满足．曲线，区域
．若为两段分离的曲线，则（ ）
A． B． C． D．
【答案】A
【解析】设，则，，所以曲线C是单位元，区域为圆环（如图），∵，∴．
20．（2012广东）对任意两个非零的平面向量α和β，定义．若平面向量满足，与的夹角，且和都在集合中，则=（ ）
A． B．1 C． D．
【答案】C
【解析】首先观察集合，从而分析和的范围如下：因为，∴，而，且，可得，又∵中，∴，从而，∴ ，所以．且也在集合中，故有．
21．（2011山东）设，，，是平面直角坐标系中两两不同的四点，
若(∈)，(∈)，且，则
称，调和分割，，已知点，，(∈)调和分割
点，，则下面说法正确的是
A．可能是线段的中点
B．可能是线段的中点
C．，可能同时在线段上
D．，不可能同时在线段的延长线上
【答案】D
【解析】根据已知得，即，从而得
；，即，得，
根据，得．线段的方程是，．
若是线段的中点，则，代入，得．
此等式不可能成立，故选项A的说法不成立；同理选项B的说法也不成立；
若同时在线段上，则，，
此时，，，若等号成立，则只能，
根据定义，是两个不同的点，故矛盾，故选项的说法也不正确，
若同时在线段的延长线上，若，，则，
与矛盾，若，则是负值，与矛盾，
若，，则，，此时，与矛盾，
故选项D的说法是正确的．
22．（2020浙江17）设，为单位向量，满足，，，设，的夹角为，则的最小值为 ▲ ．
【答案】
【思路导引】利用复数模的平方等于复数的平方化简条件得，再根据向量夹角公式求函数关系式，根据函数单调性求最值．
【解析】，解得：，
，
设，
则，
当时，，∴的最小值是，故答案为： ．
23．（2020北京13）已知正方形的边长为，点满足，则 ________；__________．
【答案】，
【解析】分别以为轴，轴建立直角坐标系，则，，，．
∵，∴，∴，
∴，又∵，∴．
24．（2020上海12）已知是平面内两两互不相等的向量，满足且（其中），则的最大值为 ．
【答案】6
【解析】根据条件不妨设，，，
，当，表示圆心为原点，半径为1的圆；
，表示圆心为原点，半径为2的圆，如图这两个圆用红色线表示；
当，表示圆心为，半径为1的圆；
，表示圆心为，半径为2的圆，如图这两个圆用蓝色线表示，
由条件可知点既要在红色曲线上，又要在蓝色曲线上，由图象可知，共有6个交点，即是最大值是6．故答案为：6．
25．（2020天津15）如图，在四边形中，，，且，则实数的值为_________，若是线段上的动点，且，则的最小值为_________．
【答案】
【思路导引】可得，利用平面向量数量积的定义求得的值，然后以点为坐标原点，所在直线为轴建立平面直角坐标系，设点，则点（其中），得出关于的函数表达式，利用二次函数的基本性质求得的最小值．
【解析】，，，
，解得，
以点为坐标原点，所在直线为轴建立如下图所示的平面直角坐标系，
则，设，则（其中），
，，
，
所以，当时，取得最小值，故答案为：；．
26．(2017浙江)已知向量，满足，，则的最小值是 ，
最大值是 ．
【答案】4，
【解析】设向量的夹角为，由余弦定理有：
，
，
则，
令，则，
据此可得：，
即的最小值是4，最大值是．
27．（2015浙江）已知是空间单位向量，，若空间向量满足，，且对于任意，，则____，_____，_____．
【答案】1 2
【解析】 由题意可令，其中，由得，由，得，解得，，∴．
28．(2014山东)在中，已知，当时，的面积为 ．
【答案】
【解析】∵，∴由，得，故的面积为．
29．（2014安徽）已知两个不相等的非零向量，，两组向量和均由2个 和3个排列而成．记
，表示所有可能取值中的最小值．则下列命题正确的是____（写出所有正确命题的编号）．
①有5个不同的值．
②若则与无关．
③若则与无关．
④若，则．
⑤若，，则与的夹角为．
【答案】②④
【解析】S有下列三种情况：
，
，
∵，
∴，
若，则，与无关，②正确；
若，则，与有关，③错误；
若，则，④正确；
若，则
∴， ∴，⑤错误．
30．（2013山东）已知向量与的夹角，且||=3，||=2，若
，且，则实数的值为_____．
【答案】
【解析】向量与的夹角为，且所以．由得，，即，所以，即，解得．
31．（2013浙江）设，为单位向量，非零向量，，若，的夹角为，则的最大值等于________．
【答案】2
【解析】
，所以的最大值为2．
32．（2013天津）在平行四边形ABCD中，AD = 1，，E为CD的中点．若， 则AB的长为 ．
【答案】
【解析】因为E为CD的中点，所以，，因为，所以，即，所以，解得．
33．（2011浙江）若平面向量，满足||=1，||≤1，且以向量，为邻边的
平行四边形的面积为，则与的夹角的取值范围是 ．
【答案】
【解析】如图，向量与在单位圆内，因||=1，||≤1，且以向量，为邻边的平行四边形的面积为，故以向量，为边的三角形的面积为，故的终点在如图的线段上（∥，且圆心到的距离为），因此夹角的取值范围为．
34．（2019江苏12）如图，在中，D是BC的中点，E在边AB上，BE=2EA，AD与CE交于点．若，则的值是 ．
【答案】
【解析】设，∴== ===，所以，解得，所以，，
，因为，所以， 所以，所以．
35．（2019浙江17）已知正方形的边长为1，当每个取遍时，的最小值是________，最大值是_______．
【答案】
【解析】正方形ABCD的边长为1，可得 QUOTE AB+AD=AC ， QUOTE BD=AD-AB ， QUOTE AB⋅AD=0 ，
，
由于 QUOTE ?i(i=1, ?i(i=1,2，3，4，5，6)取遍 QUOTE ±1 ，可得 QUOTE λ1-λ3+λ5-λ6=0 ， QUOTE λ2-λ4+λ5+λ6=0 ，可取 QUOTE λ5=λ6=1 ， QUOTE λ1=λ3=1 可得所求最小值为0；
由 QUOTE λ1-λ3+λ5-λ6 ， QUOTE λ2-λ4+λ5+λ6 ，可取 QUOTE λ2=1 QUOTE λ5=λ6=1 QUOTE λ1=1 QUOTE λ3=-1 可得所求最大值为 QUOTE 25 ．
36．（2019天津理14）在四边形中，，点在线段的延长线上，且，则 ．
【答案】-1
【解析】因为，，，所以在等腰三角形中，，
又，所以，所以，因为，所以，又，
所以
．
37．(2018上海)在平面直角坐标系中，已知点，，，是轴上的两个动点，且，则的最小值为______．
【答案】
【解析】设，，所以= ，当时，取得最小值．
38．（2017江苏）在平面直角坐标系中，，，点在圆：上，若，则点的横坐标的取值范围是 ．
【答案】
【解析】设，由，得，如图由可知，在上，由，解得，，所以点横坐标的取值范围为．
39．（2016年浙江）已知向量，，，若对任意单位向量，均有
，则的最大值是 ．
【答案】
【解析】由题意令，，，则由 可得 ①，令 ②，得对一切实数恒成立，所以．故 ≤，故最大值为．
40．（2015天津）在等腰梯形中，已知，，，．
动点和分别在线段和上，且，，则的最小值为 ．
【答案】
【解析】 因为，，∴= =，∴，
，
当且仅当即时的最小值为．
41．（2015江苏）设向量，则的值为 ．
【答案】
【解析】 =，因此．
42．（2014湖南）在平面直角坐标系中，为原点，动点满足，则的最大值是 ．
【答案】
【解析】设，由，得，向量
，故
的最大值为圆上的动点到点距离的最大值，
其最大值为圆的圆心到点的距离加上圆的半径，
即．
43．（2012江苏）如图，在矩形中，点为的中点，点在边上，若，则的值是 ．
【答案】
【解析】以为坐标原点，，所在的直线分别为，轴建立直角坐标系，则，，，．设(0≤≤)，由，∴，=((1，2)=．
44．（2012山东）如图，在平面直角坐标系中，一单位圆的圆心的初始位置在，此时圆上一点的位置在，圆在轴上沿正向滚动．当圆滚动到圆心位于时，的坐标为 ．
【答案】
【解析】如图过P作x轴的垂线，垂足为E，过C作y轴的垂线，垂足为A，根据题意可知圆滚动了2个单位的弧长，∴，可知，此时点的坐标为
∴即．
45．（2017江苏）已知向量，，．
（1）若，求的值；
（2）记，求的最大值和最小值以及对应的的值．
【解析】（1）因为，，，
所以．
若，则，与矛盾，故．
于是．
又，所以．
（2）．
因为，所以，
从而．
于是，当，即时，取到最大值3；
当，即时，取到最小值．
46．（2015广东）在平面直角坐标系中，已知向量，，
．
（1）若，求的值；
（2）若与的夹角为，求的值．
【解析】(1)∵，∴，故，∴．
（2）∵与的夹角为，∴，
故，又，∴，，即．
故的值为．
47．（2014山东）已知向量，函数，且
的图像过点和点．
（Ⅰ）求的值；
（Ⅱ）将的图像向左平移个单位后得到函数
的图像，若图像上各最高点到点的距离的最小值为1，
求的单调递增区间．
【解析】（Ⅰ）已知，
过点，∴

∴ 解得
（Ⅱ）由（Ⅰ）知
由题意知
设的图象上符合题意的最高点为
由题意知．所以，即到点的距离为1的最高点为．
将其代入得，
又∵，所以，
因此
由， 得
∴的单调增区间为．
48．（2014辽宁）在中，内角的对边，且，已知，
，，求：
（Ⅰ）和的值；
（Ⅱ）的值．
【解析】（Ⅰ）∵，
且，∴，∵，∴解得．
所以．
（Ⅱ）∵，∴，∵，
，，
∴，故．
49．（2013江苏）已知，，．
(1) 若，求证：；
(2) 设，若，求，的值．
【解析】（1）＝，
＝
＝．
所以，，所以，．
（2），①2＋②2得：．
所以，＝，＝＋，
带入②得：(＋)＋＝＋＝(＋)＝1，
所以，＋＝．所以，＝，＝．
50．（2013辽宁）设向量
（ = 1 \* ROMAN I）若，求的值；
（ = 2 \* ROMAN II）设函数，求的最大值．
【解析】（I）由，
，及
又，所以．
（II）
=．
当所以 年 份
题号
考 点
考 查 内 容
2011
课标
理10
平面向量的综合应用
利用平面向量数量积计算向量夹角与模问题及命题真假的判定
文13
平面向量数量积性质的应用
利用平面向量数量积处理向量垂直问题
2012
课标
理13
文15
平面向量数量积性质的应用
平面向量的定义及利用平面向量数量积处理向量模问题
2013
卷1
理13
文13
平面向量数量积的概念及其几何意义
平面向量数量积的概念及运算法则
卷2
理13
文14
平面向量数量积的概念及其几何意义
平面向量数量积的运算法则
2014
卷1
理15
平面向量数量积的概念及其几何意义
中点公式的向量形式及向量的夹角的概念
卷2
文4
理3
平面向量数量积性质的应用
利用平面向量数量积处理向量模问题
2015
卷1
理5
平面向量的综合应用
主要与双曲线结合考查平面向量数量积的坐标运算
卷2
文4
平面向量数量积的概念及其几何意义
平面向量的坐标运算、平面向量数量积
2016
卷1
理13
平面向量数量积性质的应用
平面向量的坐标运算及平面向量模公式
卷2
理3
平面向量数量积性质的应用
平面向量的坐标运算及利用平面向量数量积处理垂直问题
卷3
理3文3
平面向量数量积的概念及其几何意义
平面向量的数量积的坐标运算及利用平面向量数量积求夹角
卷1
文13
平面向量数量积性质的应用
平面向量的坐标运算及利用平面向量数量积处理垂直问题
2017
卷1
理13
平面向量数量积性质的应用
利用平面向量数量积计算模
理2
理12
平面向量的综合应用
与平面图形有关的平面向量数量积的最值问题
卷1
文13
平面向量数量积性质的应用
利用平面向量数量积的坐标运算及利用向量数量积处理垂直问题
卷2
文4
平面向量数量积性质的应用
利用平面向量数量积的模
卷3
理12
平面向量的综合应用
向量的坐标运算以及圆的方程和三角函数的性质
卷3
文13
平面向量数量积性质的应用
平面向量的坐标运算及利用平面向量数量积处理垂直问题
2018
卷2
理4文4
平面向量数量积的概念、几何意义及其运算律
平面向量的数量积及其运算律
2019
卷1
理7
文8
平面向量数量积性质的应用
平面向量数量积处理垂直与夹角问题
卷2
理3
平面向量的综合应用
平面向量的减法运算、模公式、平面向量数量积
卷3
理13
平面向量的综合应用
平面向量数量积处理模与夹角问题
卷3
理13
平面向量数量积性质的应用
平面向量坐标的模公式及夹角公式
2020
卷1
理14
平面向量数量积及其运算
向量模长的计算
文14
平面向量数量积的应用
平面向量垂直充要条件的坐标形式，平面向量数量积的应用
卷2
理13
平面向量数量积的应用
向量夹角公式，应用向量数量积处理垂直问题
文15
平面向量数量积定义及性质
平面向量数量积的定义和运算性质，应用平面向量数量积处理向量垂直
卷3
理6
平面向量数量积及其运算
平面向量夹角公式，平面向量数量积的计算以及向量模长的计算
考 点
出现频率
2021年预测
考点51平面向量数量积的概念及其几何意义
7/24
2021年高考仍将重点单独或与平面图形等知识结合重点平面向量数量积的定义、性质及应用平面向量数量积计算夹角、模、垂直等问题，难度为基础题、中档题或难题，题型为选择或填空．
考点52平面向量数量积性质的应用
9/24
考点53平面向量的综合应用
8/24