初中数学人教版八年级下册18.2.2 菱形同步达标检测题

这是一份初中数学人教版八年级下册18.2.2 菱形同步达标检测题，文件包含第3讲特殊图形的旋转与弦图--提高班教师版docx、第3讲特殊图形的旋转与弦图--提高班学生版docx等2份试卷配套教学资源，其中试卷共20页， 欢迎下载使用。
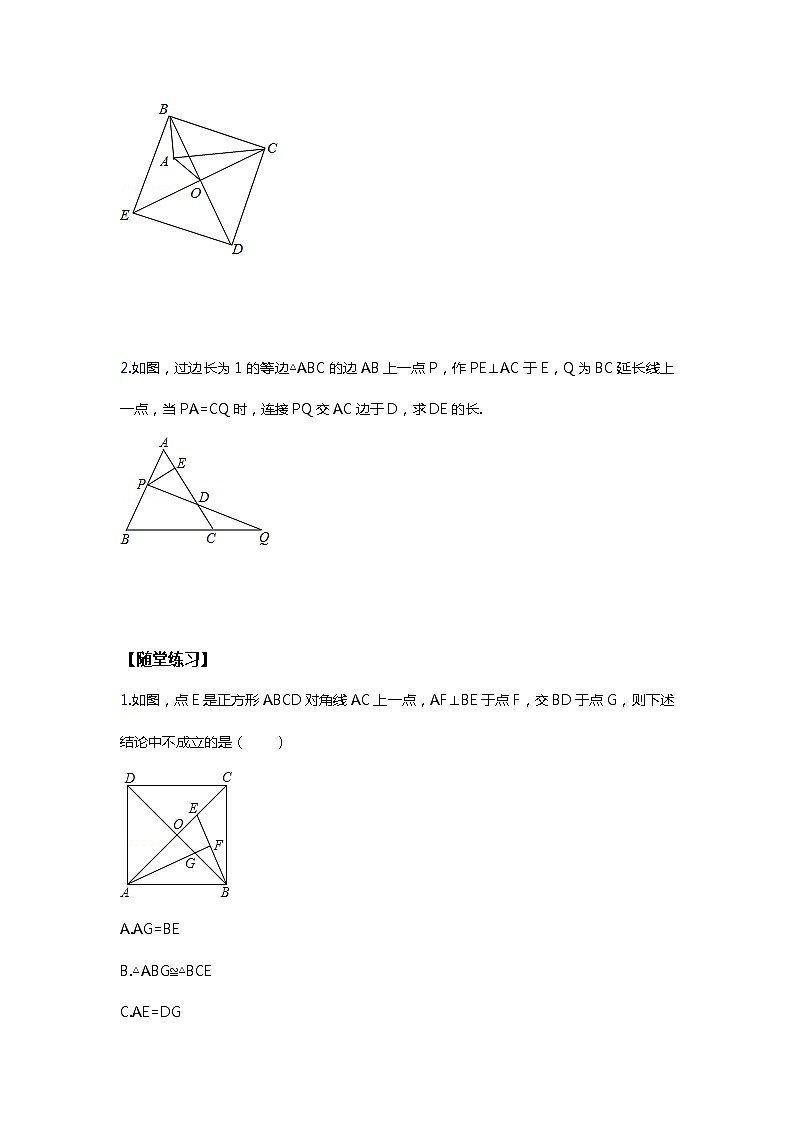
初二数学人教版下册春季班第3讲  勾股定理的综合知识点1 复杂的“旋转型”在一些特殊图形中，由两边相等可以利用“旋转”的方式将三角形“转移”，从而达到转移边或角的目的.在没有明确给出“旋转”后的图形时，有的需要作辅助线进行构造. 常见的一些模型如下：【典例】1.如图，以Rt△ABC的斜边BC为一边作正方形BCDE，对角线的交点为O，连接AO，如果AB=3，AO=，求AC的长.    2.如图，过边长为1的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当PA=CQ时，连接PQ交AC边于D，求DE的长.  【随堂练习】1.如图，点E是正方形ABCD对角线AC上一点，AF⊥BE于点F，交BD于点G，则下述结论中不成立的是（　　）A.AG=BE B.△ABG≌△BCE C.AE=DG D.∠AGD=∠DAG2.如图，点E是边长为5的正方形ABCD外一点，点F是线段AE上一点，△EBF是等腰直角三角形，其中∠EBF=90°，连接CE、CF．若EF=6，则CF的长为（　　）  3.如图，D是等边△ABC的边AC上的一点，E是等边△ABC外一点，若BD=CE，∠1=∠2，则对△ADE的形状最准确的是（　　）A.等腰三角形B.直角三角形 C.等边三角形 D.不等边三角形 知识点2 弦图及其拓展“赵爽弦图”是由四个全等的直角三角形拼成一个大的正方形，如下图.图中的等量关系有：a2+b2=c2；4个小三角形的面积和=2ab；大正方形的边长为c，面积= a2+b2=c2；小正方形的边长为b-a=，面积= （b-a）2=c2﹣2ab；（a+b）2=a2+b2+2ab=c2+2ab；（a-b）2=a2+b2-2ab=c2-2ab.【典例】例1（2020春•西市区期末）如图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若，，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到如图2所示的“数学风车”，则这个风车的外围周长是　　A．76 B．72 C．68 D．52  例2 （2020秋•武侯区校级月考）中国古代数学家们对于勾股定理的发现和证明，在世界数学史上具有独特的贡献和地位，体现了数学研究中的继承和发展，现用4个全等的直角三角形拼成如图所示“弦图”． 中，．，，，请你利用这个图形解决下列问题：（1）试说明：；（2）如果大正方形的面积是13，小正方形的面积是3，求的值．  【随堂练习】1．（2020春•番禺区校级月考）如图是“赵爽弦图”， 、、和是四个全等的直角三角形，四边形和是正方形，如果，，那么　　． 2．我国魏晋时期的数学家赵爽在为天文学著作《周髀算经》作注解时，用4个全等的直角三角形拼成如图所示的正方形，并用它证明了勾股定理，这个图被称为“弦图”．它体现了中国古代的数学成就，是我国古代数学的骄傲．正因为此，这个图案被选为2002年在北京召开的国际数学家大会的会徽．请你利用“弦图”证明勾股定理．     综合运用1．（2020秋•法库县期末）如图是“赵爽弦图”， ，，和是四个全等的直角三角形，四边形和都是正方形，如果，，那么　　．  2．（2020秋•蕉城区期中）我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”，它是用八个全等的直角三角形拼接而成，记图中正方形，正方形，正方形的面积分别为，，．若正方形的边长为，则　　．  3．（2020春•临江市校级期末）图1是我国著名的“赵爽弦图”，它由四个全等的直角三角形所围成．将四个直角三角形的较短边（如向外延长与此边长相等的长度得到点，，，，得到图2．已知正方形与正方形的面积分别为和，则阴影部分的面积为　　．