初中人教版12.1 全等三角形当堂达标检测题

这是一份初中人教版12.1 全等三角形当堂达标检测题，共6页。

【学习目标】
1．理解和掌握全等三角形判定方法3——“边边边”，和判定方法4——“角角边”；
2．能把证明角相等或线段相等的问题，转化为证明它们所在的两个三角形全等.
【要点梳理】
要点一、全等三角形判定3——“边边边”
全等三角形判定1——“边边边”
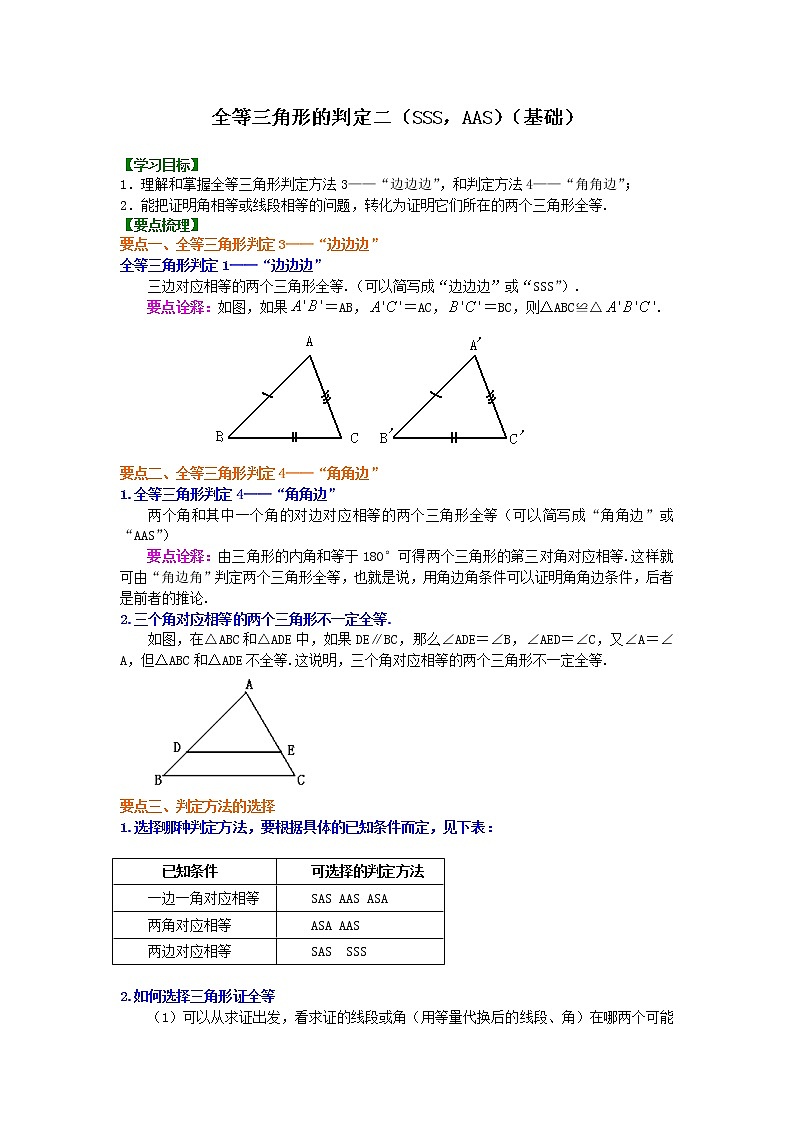
三边对应相等的两个三角形全等.（可以简写成“边边边”或“SSS”）.
要点诠释：如图，如果＝AB，＝AC，＝BC，则△ABC≌△.

要点二、全等三角形判定4——“角角边”
1.全等三角形判定4——“角角边”
两个角和其中一个角的对边对应相等的两个三角形全等（可以简写成“角角边”或“AAS”）
要点诠释：由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等，也就是说，用角边角条件可以证明角角边条件，后者是前者的推论.
2.三个角对应相等的两个三角形不一定全等.
如图，在△ABC和△ADE中，如果DE∥BC，那么∠ADE＝∠B，∠AED＝∠C，又∠A＝∠A，但△ABC和△ADE不全等.这说明，三个角对应相等的两个三角形不一定全等.
要点三、判定方法的选择
1.选择哪种判定方法，要根据具体的已知条件而定，见下表：
2.如何选择三角形证全等
（1）可以从求证出发，看求证的线段或角（用等量代换后的线段、角）在哪两个可能全等的三角形中，可以证这两个三角形全等；
（2）可以从已知出发，看已知条件确定证哪两个三角形全等；
（3）由条件和结论一起出发，看它们一同确定哪两个三角形全等，然后证它们全等；
（4）如果以上方法都行不通，就添加辅助线，构造全等三角形.
【典型例题】
类型一、全等三角形的判定3——“边边边”
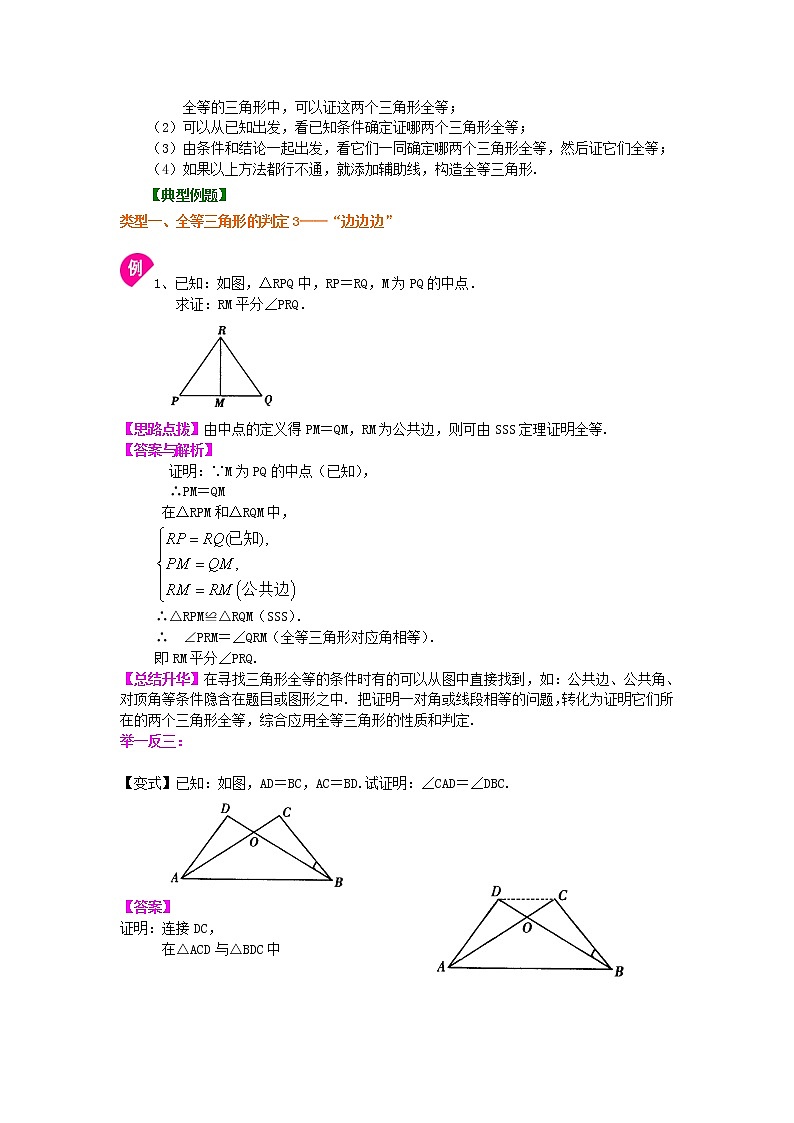
1、已知：如图，△RPQ中，RP＝RQ，M为PQ的中点．
求证：RM平分∠PRQ．
【思路点拨】由中点的定义得PM＝QM，RM为公共边，则可由SSS定理证明全等.
【答案与解析】
证明：∵M为PQ的中点（已知），
∴PM＝QM
在△RPM和△RQM中，
∴△RPM≌△RQM（SSS）．
∴ ∠PRM＝∠QRM（全等三角形对应角相等）．
即RM平分∠PRQ.
【总结升华】在寻找三角形全等的条件时有的可以从图中直接找到，如：公共边、公共角、对顶角等条件隐含在题目或图形之中. 把证明一对角或线段相等的问题，转化为证明它们所在的两个三角形全等，综合应用全等三角形的性质和判定.
举一反三：
【变式】已知：如图，AD＝BC，AC＝BD.试证明：∠CAD＝∠DBC.
【答案】
证明：连接DC，
在△ACD与△BDC中
∴△ACD≌△BDC（SSS）
∴∠CAD＝∠DBC（全等三角形对应角相等）
类型二、全等三角形的判定4——“角角边”
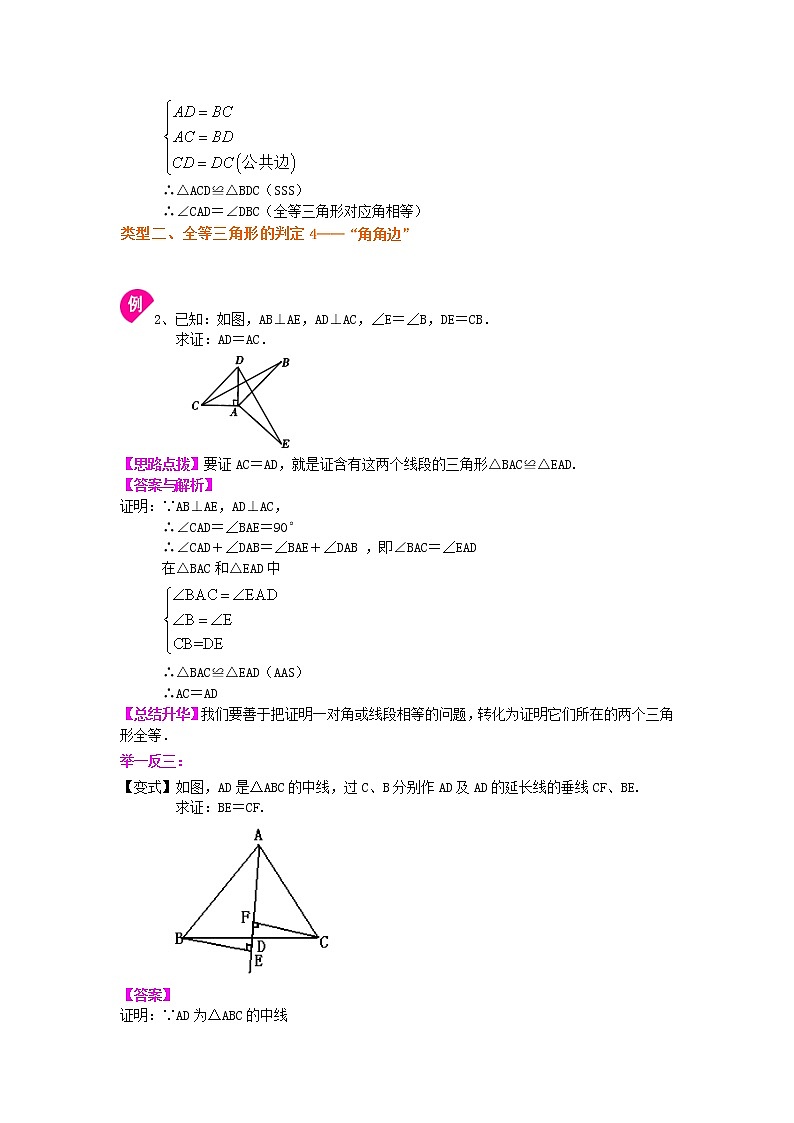
2、已知：如图，AB⊥AE，AD⊥AC，∠E＝∠B，DE＝CB．
求证：AD＝AC．
【思路点拨】要证AC＝AD，就是证含有这两个线段的三角形△BAC≌△EAD.
【答案与解析】
证明：∵AB⊥AE，AD⊥AC，
∴∠CAD＝∠BAE＝90°
∴∠CAD＋∠DAB＝∠BAE＋∠DAB ，即∠BAC＝∠EAD
在△BAC和△EAD中

∴△BAC≌△EAD（AAS）
∴AC＝AD
【总结升华】我们要善于把证明一对角或线段相等的问题，转化为证明它们所在的两个三角形全等．
举一反三：
【变式】如图，AD是△ABC的中线，过C、B分别作AD及AD的延长线的垂线CF、BE.
求证：BE＝CF.
【答案】
证明：∵AD为△ABC的中线
∴BD＝CD
∵BE⊥AD，CF⊥AD，
∴∠BED＝∠CFD＝90°，
在△BED和△CFD中
∴△BED≌△CFD（AAS）
∴BE＝CF
3、（2020春•雅安期末）如图：AB=A′B′，∠A=∠A′，若△ABC≌△A′B′C′，则还需添加的一个条件有（ ）种．
A.1B. 2C.3D.4
【思路点拨】本题要证明△ ABC≌△ A′B′C′，已知了AB=A′B′，∠ A=∠ A′，可用的判别方法有ASA，AAS，及SAS，所以可添加一对角∠B=∠B′，或∠C=∠C′，或一对边AC=A′C′，分别由已知与所添的条件即可得证．
【答案与解析】
解：添加的条件可以为：
∠B=∠B′；∠C=∠C′；AC=A′C′，共3种．
若添加∠B=∠B′，
证明：在△ABC和△A′B′C′中，
，
∴△ABC≌△A′B′C′（ASA）；
若添加∠C=∠C′，
证明：在△ABC和△A′B′C′中，
，
∴△ABC≌△A′B′C′（AAS）；
若添加AC=A′C′，
证明：在△ABC和△A′B′C′中，
，
∴△ABC≌△A′B′C′（SAS）．
故选C.
【总结升华】此题考查了全等三角形的判定，是一道条件开放型问题，需要由因索果，逆向推理，逐步探求使结论成立的条件，解决这类问题要注意挖掘隐含的条件，如公共角、公共边、对顶角相等，这类问题的答案往往不唯一，只有合理即可．熟练掌握全等三角形的判定方法是解本题的关键．
类型三、全等三角形判定的实际应用
4、“三月三，放风筝”．下图是小明制作的风筝，他根据DE＝DF，EH＝FH，不用度量，就知道∠DEH＝∠DFH．请你用所学的知识证明．
【答案与解析】
证明：在△DEH和△DFH中，

∴△DEH≌△DFH(SSS)
∴∠DEH＝∠DFH．
【总结升华】证明△DEH≌△DFH，就可以得到∠DEH＝∠DFH，我们要善于从实际问题中抽离出来数学模型，这道题用“SSS”定理就能解决问题.
举一反三：
【变式】（2020秋•紫阳县期末）雨伞的中截面如图所示，伞骨AB=AC，支撑杆OE=OF，AE=AB，AF=AC，当O沿AD滑动时，雨伞开闭，问雨伞开闭过程中，∠BAD与∠CAD有何关系？说明理由．
【答案】
解：雨伞开闭过程中二者关系始终是：∠BAD=∠CAD，
理由如下：
∵AB=AC，AE=AB，AF=AC，
∴AE=AF，
在△AOE与△AOF中，
，
∴△AOE≌△AOF（SSS），
∴∠BAD=∠CAD． 已知条件
可选择的判定方法
一边一角对应相等
SAS AAS ASA
两角对应相等
ASA AAS
两边对应相等
SAS SSS