2022长沙南雅中学高二下学期期中考试数学含解析

这是一份2022长沙南雅中学高二下学期期中考试数学含解析，文件包含湖南省长沙市南雅中学2021-2022学年高二下学期期中数学试题含解析docx、湖南省长沙市南雅中学2021-2022学年高二下学期期中数学试题无答案docx等2份试卷配套教学资源，其中试卷共25页， 欢迎下载使用。
1 已知全集，集合，则（ ）
A. B. C. D.
2.
A. B. C. D.
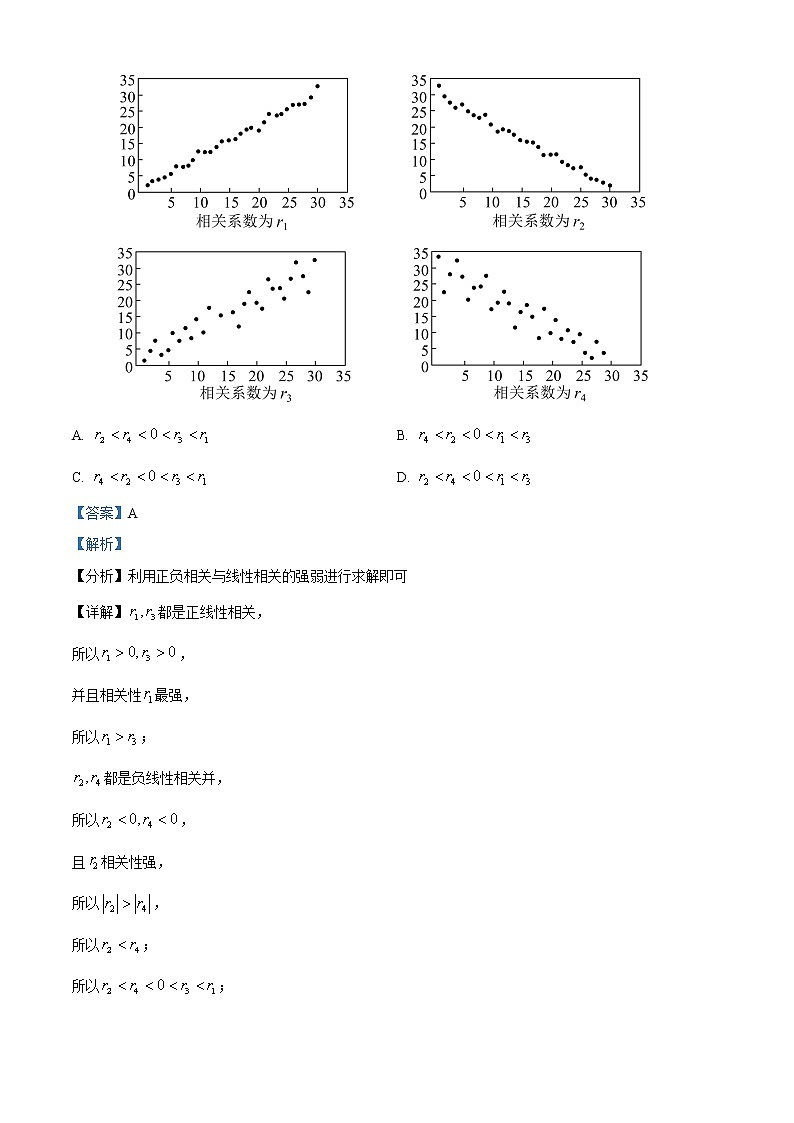
3. 对四组数据进行统计，获得以下散点图，关于其相关系数的比较，正确的是（ ）
A. B.
C. D.
4. 函数的一个递减区间是（ ）
A. B. C. D.
5. 已知圆柱的侧面积为，体积为则该圆柱的轴截面的面积为（ ）
A. B. C. D.
6. 已知，且，则（ ）
A. B.
C. D.
7. 一试验田某种作物一株的生长果实个数x服从正态分布，且，从试验田中随机抽取20株，果实个数在[的株数记作随机变量X，且X服从二项分布，则X的方差为（ ）
A. 0.42B. 0.6C. 4.2D. 6
8. 已知是定义域为R的偶函数，，，.若是偶函数，则（ ）
A. －3B. －2C. 2D. 3
二､多选题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.
9. 记为等差数列的前n项和．已知，则
A. B. C. D.
10. 若函数，则（ ）
A. 定义域是
B. 有两个零点
C. 在点处切线的斜率为
D. 在递增
11. 已知由样本数据点集合，求得的回归直线方程为，且，现发现两个数据点和误差较大，去除后重新求得的回归直线l的斜率为1.2，则（ ）
A. 变量x与y具有正相关关系B. 去除后的回归方程为
C. 去除后y的估计值增加速度变快D. 去除后相应于样本点的残差为0.05
12. 已知抛物线C：，圆F：（F为圆心），点P在抛物线C上，点Q在圆F上，点A，则下列结论中正确的是（ ）
A. 的最小值是B. 的最小值是
C. 当最大时，D. 当最小时，
三､填空题：本题共4小题，每小题5分，共20分.
13. 已知函数是R上的偶函数，则实数m的值为___________.
14. 的展开式中的系数为__________．
15. 已知平面向量，，.若与共线，则在上的投影向量的坐标为___________.
16. 设双曲线C：左焦点和右焦点分别是，，点A是C右支上的一点，则的最小值为___________.
四､解答题：本题共6小题，共70分，解答应写出文字说明､证明过程或演算步骤.
17. 已知数列满足，且对于任意，，都有.
（1）求的通项公式；
（2）设，求数列的前项和.
18. 在中，.
（1）求角的大小；
（2）若，的面积为，求的周长.
19. “五项管理”是“双减”工作的一项具体抓手，是促进学生身心健康､解决群众急难愁盼问题的重要举措.为了在“控量”的同时力求“增效”，提高作业质量，某学校计划设计差异化作业.因此该校对初三年级的400名学生每天完成作业所用时间进行统计，部分数据如下表：
（1）求x，y，z的值，并根据题中的列联表，判断是否有95%的把握认为完成作业所需时间在90分钟以上与性别有关？
（2）教务处从完成作业所需时间在90分钟以上的学生中用分层抽样的方法抽取9人了解情况，校长再从这9人中选取3人进行访谈，记校长选取的3人中男生人数为X，求X的分布列和数学期望.
附：
20. 如图，在四棱台中，底面四边形ABCD是矩形，，平面平面ABCD，平面平面ABCD.
（1）求证：平面ABCD；
（2）若二面角的余弦值为，求四棱台的高.
21. 已知椭圆E：的一个焦点与短轴的两个端点是正三角形的三个顶点，直线与椭圆相交于两点P和Q，且.
（1）求椭圆E的方程；
（2）设不过原点O且斜率为的直线与椭圆E交于不同的两点A，B，线段AB的中点为M，直线OM与椭圆E交于C，D.证明：
22. 已知函数，.
（1）当时，讨论的单调性；
（2）当时，函数最小值为（其中为的导函数），求的值.男生
女生
总计
90分钟以上
80
180
90分钟以下
220
总计
160
240
400
0.150
0100
0.050
0.025
0.010
2.072
2.076
3.841
5.024
6.635