初中数学苏科版七年级下册7.1 探索直线平行的条件精品课时练习

这是一份初中数学苏科版七年级下册7.1 探索直线平行的条件精品课时练习，文件包含专题01探索直线平行的条件压轴题五种模型全攻略解析版docx、专题01探索直线平行的条件压轴题五种模型全攻略原卷版docx等2份试卷配套教学资源，其中试卷共31页， 欢迎下载使用。

目录
TOC \ "1-3" \h \u \l "_Tc6588" 【典型例题】 PAGEREF _Tc6588 \h 1
\l "_Tc12430" 考点一 同位角、内错角、同旁内角的辨别 PAGEREF _Tc12430 \h 1
\l "_Tc25801" 考点二 同位角相等，两直线平行 PAGEREF _Tc25801 \h 2
\l "_Tc17777" 考点三 内错角相等，两直线平行 PAGEREF _Tc17777 \h 4
\l "_Tc13604" 考点四 同旁内角互补，两直线平行 PAGEREF _Tc13604 \h 6
\l "_Tc21494" 考点五 添加一条件使两条直线平行 PAGEREF _Tc21494 \h 7
\l "_Tc1262" 【过关检测】 PAGEREF _Tc1262 \h 8
【典型例题】
考点一 同位角、内错角、同旁内角的辨别
例题：（2022·全国·七年级课前预习）如图，在所标识的角中，∠1与____是同位角，∠2与_____是内错角，∠5与____是同旁内角．
【答案】 ∠4 ∠3 ∠3
【解析】略
【变式训练】
1．（2021·全国·七年级课时练习）如图所示，与是_________角，是直线________和直线________被直线_____所截而形成的，与是_____角，是直线________和直线___________被直线__________所截而形成的．
【答案】 内错 AB CB AC 同旁内 AC BC AB
【分析】根据三线八角中的内错角，同旁内角定义即可得出答案．
【详解】解：如图所示，与是内错角，是直线AB和直线CB被直线AC所截而形成的，
与是同旁内角，是直线AC和直线BC被直线AB所截而形成的．
故答案为内错；AB；CB；AC；同旁内；AC；BC；AB．
【点睛】本题考查三线八角中的内错角，同旁内角，掌握三线八角中的截线与被截直线，内错角与同旁内角．
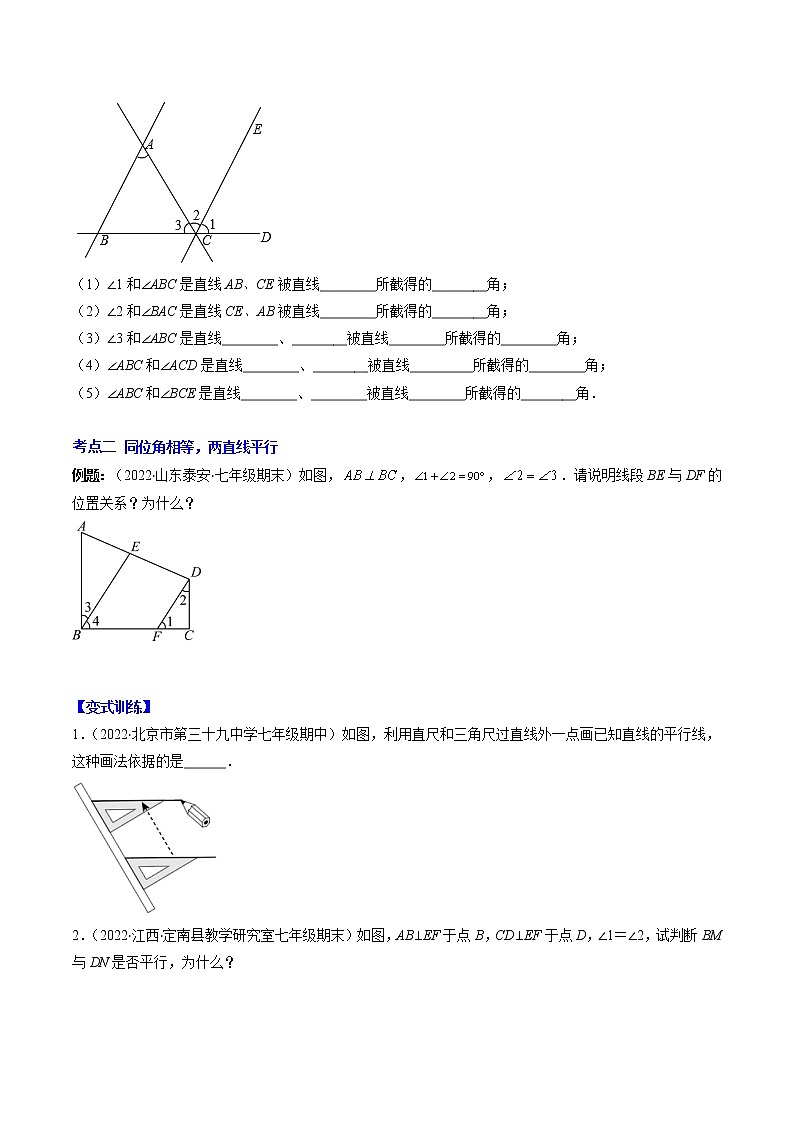
2．（2022·全国·七年级）如图，
（1）∠1和∠ABC是直线AB、CE被直线________所截得的________角；
（2）∠2和∠BAC是直线CE、AB被直线________所截得的________角；
（3）∠3和∠ABC是直线________、________被直线________所截得的________角；
（4）∠ABC和∠ACD是直线________、________被直线_________所截得的________角；
（5）∠ABC和∠BCE是直线________、________被直线________所截得的________角．
【答案】 BD（BC） 同位 AC 内错 AB AC BC 同旁内 AB AC BC 同位 AB CE BC 同旁内
【分析】根据同位角、内错角、同旁内角的性质判断即可；
【详解】（1）∠1和∠ABC是直线AB、CE被直线BD（BC）所截得的同位角；
（2）∠2和∠BAC是直线CE、AB被直线AC所截得的内错角；
（3）∠3和∠ABC是直线AB、AC被直线BC所截得的同旁内角；
（4）∠ABC和∠ACD是直线AB、AC被直线BC所截得的同位角；
（5）∠ABC和∠BCE是直线AB、CE被直线BC所截得的同旁内角．
故答案是：BD（BC）；同位；AC；内错；AB；AC；BC；同旁内；AB；AC；BC；同位；AB；CE；BC；同旁内．
【点睛】本题主要考查了同位角、内错角、同旁内角的判断，准确分析判断是解题的关键．
考点二 同位角相等，两直线平行
例题：（2022·山东泰安·七年级期末）如图，，，．请说明线段BE与DF的位置关系？为什么？
【答案】BEDF，见解析
【分析】由已知推出∠3+∠4=90°，利用，，得到∠1=∠4，即可得到结论BEDF．
【详解】解：BEDF，
∵，
∴∠ABC=90°，
∴∠3+∠4=90°，
∵，，
∴∠1=∠4，
∴BEDF．
【点睛】此题考查了平行线的判定定理，熟记平行线的判定定理并熟练应用是解题的关键．
【变式训练】
1．（2022·北京市第三十九中学七年级期中）如图，利用直尺和三角尺过直线外一点画已知直线的平行线，这种画法依据的是______．
【答案】同位角相等，两直线平行
【分析】利用同位角相等，两直线平行画一条直线与原直线平行．
【详解】解：在图中画两个相等的同位角，则可判断所画直线与原直线平行．
故答案为同位角相等，两直线平行．
【点睛】本题考查了作图复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．
2．（2022·江西·定南县教学研究室七年级期末）如图，AB⊥EF于点B，CD⊥EF于点D，∠1＝∠2，试判断BM与DN是否平行，为什么？
【答案】；理由见解析
【分析】根据AB⊥EF，CD⊥EF， 得出∠ABE＝∠CDE＝90°，根据∠1＝∠2，得出∠MBE＝∠NDE，即可得出．
【详解】；理由如下：
∵AB⊥EF，CD⊥EF，
∴∠ABE＝∠CDE＝90°(垂直的定义)，
∵∠1＝∠2，
∴∠ABE－∠1＝∠CDE－∠2，
即∠MBE＝∠NDE，
∴ (同位角相等，两直线平行)．
【点睛】本题主要考查了垂直的定义，余角的性质，平行线的判定，根据题意得出∠MBE＝∠NDE，是解题的关键．
考点三 内错角相等，两直线平行
例题：（2022·山东·曲阜九巨龙学校七年级阶段练习）如图，点A在直线DE上，AB⊥AC于A，∠1与∠C互余，DE和BC平行吗？若平行，请说明理由．
【答案】平行，理由见解析
【分析】由垂直定义可得∠BAC=90°，根据平角定义得∠1+∠BAC+∠CAE=180°，即可得出∠1+∠CAE=90°，由∠1与∠C互余，根据余角的性质即可得出∠CAE=∠C，根据平行线的判定定理即可得出结论．
【详解】解：平行， 理由如下：
∵AB⊥AC，
∴∠BAC=90°，
∵∠1+∠BAC+∠CAE=180°，
∴∠1+∠CAE=90°，
∵∠1与∠C互余，即∠1+∠C=90°，
∴∠CAE=∠C，
∴DEBC．
【点睛】本题考查平行线的判定，余角的性质，熟练掌握平行线的判定定理是解题的关键．
【变式训练】
1．（2022·云南·弥渡县弥城镇中心学校七年级期中）已知如图所示，，点、、在同一条直线上，，且平分，试说明的理由．
【答案】见解析
【分析】根据角平分线定义求出∠1＝∠EAC，根据已知求出∠C＝∠EAC，推出∠C＝∠1，根据平行线的判定得出结论．
【详解】理由：∵AD平分∠EAC，
∴∠1＝∠EAC，
∵∠EAC＝∠B＋∠C，∠B＝∠C，
∴∠C＝∠EAC，
∴∠C＝∠1，
∴ADBC．
【点睛】本题考查了角平分线定义和平行线的判定，关键是根据定理和已知推出∠1＝∠C，题目比较典型，难度不大．
2．（2022·福建·武平县实验中学七年级期中）如图，∠1＝∠C，AC平分∠DAB，求证：．
【答案】证明见解析
【分析】根据角平分线的定义得出∠1＝∠2，再利用内错角相等，两直线平行证明即可．
【详解】证明：∵AC平分∠DAB，
∴∠1＝∠2，
∵∠1＝∠C，
∴∠2＝∠C，
∴．
【点睛】此题考查平行线的判定，关键是根据角平分线的定义得出∠1＝∠2．
考点四 同旁内角互补，两直线平行
例题：（2022·西藏昂仁县中学七年级期中）如图，∠CAD＝20°，∠B＝70°，AB⊥AC，求证：ADBC．
【答案】见解析
【分析】根据同旁内角互补，两直线平行证明即可．
【详解】解：∵AB⊥AC，
∴∠BAC=90°，
∵∠CAD＝20°，∠B＝70°，
∴∠B+∠BAD=70°+90°+20°=180°，
∴ADBC．
【点睛】本题考查平行线的判定、垂直定义，熟练掌握平行线的判定方法是解答的关键．
【变式训练】
1．（2022·江苏·吕良中学七年级阶段练习）如图，直线与射线相交于点O，，直线与平行吗？为什么？
【答案】ABCD，理由见解析
【分析】先由对顶角性质得∠AOD=∠BOE=130°，再计算∠AOD+∠D=180°，即可得出结论．
【详解】解：ABCD，
理由：∵∠AOD=∠BOE=130°（对顶角相等），
∴∠AOD+∠D=130°+50°=180°，
∴ABCD(同旁内角互补，两直线平行)．
【点睛】本题考查平行线的判定，对顶角性质，熟练掌握平行线的判定定理是解题的关键．
2．（2022·山东·聊城市东昌府区博雅学校七年级阶段练习）如图，射线BC平分∠ABD，且∠1=110°，∠2=70°．求证：AB∥CD．
【答案】见解析
【分析】先根据角平分线的定义和对顶角相等可得出∠ABC=∠2=70°，再由对顶角相等可得出∠1=∠BCE=110°，则∠ABC+∠BCE=180°，由此可得出结论．
【详解】证明：∵射线BC平分∠ABD，
∴∠ABC=∠2，
∵∠1=110°，∠2=70°，∠1=∠BCE，
∴∠ABC=70°，∠BCE=110°，
∴∠ABC+∠BCE=180°，
∴AB∥CD．
【点睛】本题考查的是平行线的判定，用到的知识点为：同旁内角互补，两直线平行．
考点五 添加一条件使两条直线平行
例题：（2022·江西赣州·七年级期中）如图，点E在AC的延长线上，若要使，则需添加条件_______（写出一种即可）
【答案】∠1=∠2 等 （写出一种即可）
【分析】根据平行线的判定定理得出直接得出即可．
【详解】解：∵当∠1 =∠2时，（内错角相等，两直线平行）；
∴若要使，则需添加条件∠1 =∠2；
故答案为：∠1=∠2．
【点睛】本题主要考查了平行线的判定，熟练掌握平行线的判定定理是解题关键．
【变式训练】
1．（2022·甘肃·临泽县第三中学七年级期中）如图，填写一个能使ABCD的条件：_________．
【答案】（答案不唯一）
【分析】根据平行线的判定定理进行解答即可．
【详解】解：填写的条件为：，
，
（内错角相等，两直线平行）．
故答案为：（答案不唯一）．
【点睛】本题考查的是平行线的判定，熟知平行线的判定定理是解答此题的关键．
2．（2022·吉林·公主岭市陶家中学七年级阶段练习）如图，要使，需补充一个条件，你认为这个条件应该是______（填一个条件即可）．
【答案】(答案不唯一）
【分析】利用两线平行的判定方法，找到一组同位角相等即可．
【详解】解：当时：，
故答案为：（答案不唯一）．
【点睛】本题考查两直线平行的判定方法．利用同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行，任选其一解题即可．
【过关检测】
一、选择题
1．（2022·重庆市万州第二高级中学九年级期中）下列图中，不是同位角的是（ ）
A．B．C．D．
【答案】D
【分析】根据同位角的定义（在被截线同一侧，截线的同一方位的两个角互为同位角）解决此题．
【详解】解：A．由图可知，，是同位角，故不符合题意．
B．由图可知，，是同位角，故不符合题意．
C．由图可知，，是同位角，故不符合题意．
D．由图可知，，不是同位角，故符合题意．
故选：D．
【点睛】本题主要考查同位角，解题的关键是熟练掌握同位角的定义．
2．（2022·浙江·之江中学七年级期中）如图所示，下列说法中，错误的是（ ）
A．∠3与∠B是同旁内角B．∠A与∠1是同位角
C．∠2与∠3是内错角D．∠1与∠B是同位角
【答案】D
【分析】根据两线被第三线所截，同旁内角，内错角和同位角的定义进行判断即可．
【详解】解：A、∠3与∠B是同旁内角，选项正确，不符合题意；
B、∠A与∠1是同位角，选项正确，不符合题意；
C、∠2与∠3是内错角，选项正确，不符合题意；
D、∠1与∠B不是同位角，选项错误，符合题意；
故选D．
【点睛】本题考查三线八角，在找角的时候，首先要确定截线，然后根据它们之间的位置关系进行确定．
3．（2022·广东·东莞市石龙第二中学七年级期中）如图，，下列结论正确的是（ ）
①若，则；
②若，则；
③若，则；
④若，则．
A．①②B．②④C．②③④D．②
【答案】B
【分析】根据平行线的判定定理，即可一一判定．
【详解】解：由，不能判定，
故①不符合题意；
，，
，
，
故②符合题意；
由，，不能判定，
故③不符合题意；
，，
，
，
故④符合题意；
故选：B．
【点睛】本题考查了平行线的判定定理，熟练掌握和运用平行线的判定定理是解决本题的关键．
4．（2022·河北石家庄·七年级期中）用两个完全一样的含30°角的三角尺画平行线，下列画出的直线a与b不一定平行的是（ ）
A．B．
C．D．
【答案】C
【分析】利用平行线的判定定理即可得到结论．
【详解】解：．根据同位角相等，两直线平行得到；故不符合题意；
B．根据内错角相等，两直线平行得到，故不符合题意；
C．画出的直线与不一定平行；故符合题意；
D．根据内错角相等，两直线平行得到；故不符合题意；
故选C．
【点睛】本题考查了平行线的判定，熟练掌握平行线的判定定理是解题的关键．
5．（2022·辽宁·朝阳市第八中学七年级期中）如图，下列条件中，不能判定的是（ ）
A．B．C．D．
【答案】A
【分析】根据平行线的判定定理即可判断求解．
【详解】解：A．∠3=∠4，根据内错角相等，两直线平行可判定AD∥CB，不可判定AB∥CD，故A符合题意；
B．∠1=∠2，根据内错角相等，两直线平行可判定AB∥CD，故B不符合题意；
C．，根据同旁内角互补，两直线平行可判定AB∥CD，故C不符合题意；
D．，根据同位角相等，两直线平行可判定AB∥CD，故D不符合题意．
故选：A．
【点睛】此题考查了平行线的判定，熟记“同旁内角互补，两直线平行”、“内错角相等，两直线平行”及“同位角相等，两直线平行”是解题的关键．
二、填空题
6．（2022·广东·黄埔学校九年级开学考试）如图，∠2的同旁内角是_____．
【答案】∠4
【分析】根据同旁内角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角进行分析即可．
【详解】解：∠2的同旁内角是∠4，
故答案为：∠4．
【点睛】此题主要考查了同旁内角的概念，关键是掌握同旁内角的边构成“U”形．
7．（2022·江苏盐城·七年级阶段练习）已知∠1=40°，则∠2=_________°时，直线a，b平行.
【答案】40
【分析】根据平行线的性质，可以得到∠1=∠2，然后根据∠1的度数，即可得到∠2的度数．
【详解】解：∵a∥b，
∴∠1=∠2，
∵∠1=40°，
∴∠2=40°，
故答案为：40．
【点睛】本题考查平行线的性质，利用数形结合的思想解答是解答本题的关键．
8．（2022·江苏泰州·七年级期中）小丽将两块完全相同的直角三角尺如图所示，拼在一起，沿着三角尺的斜边画出线段AB和CD，则小丽判定ABCD，她的依据是______．
【答案】内错角相等，两直线平行
【分析】根据内错角相等，两直线平行即可判断．
【详解】解：由题意：∠BCD=∠ABC=30°，
∴ABCD（内错角相等，两直线平行），
故答案为：内错角相等，两直线平行．
【点睛】本题考查了平行线的判定，掌握平行线的判定定理是解题的关键．
9．（2022·湖北湖北·七年级期中）如图，在四边形ABCD中，点E是AB延长线上一点，请添加一个条件，使AB//CD，那么可以添加的条件是________（写出一个即可）．
【答案】（答案不唯一）
【分析】根据平行线的判定定理添加条件即可．
【详解】解：根据内错角相等，两直线平行，可添加或等条件，
故答案为：（答案不唯一）．
【点睛】本题考查平行线的判定，解题的关键是熟练掌握平行线的判定定理．
10．（2022·江西南昌·七年级期末）如图，将一副三角板按如图放置，则下列结论：①；②当时，则有；③当时，则有；④当时，则有．其中正确的序号是______．
【答案】②③④
【分析】根据∠CAB=∠EAD=90°及∠1=∠CAB-∠2，∠3=∠EAD-∠2，根据等量代换即可判断①；当，可得∠2和∠3的度数，利用内错角相等即可判断②；当时，可求得∠1，根据∠1=∠E内错角相等即可判断③；当时，∠3+∠D=90°即可判断④．
【详解】解：∵∠CAB=∠EAD=90°，∠1=∠CAB-∠2，∠3=∠EAD-∠2，
∴∠1=∠3，故①错误；
当，∠2=90°-∠1=45°，∠3=90°-∠2=45°，且∠B=45°，
因此∠B=∠3，
∴，故②正确；
当时，则∠1=90°-∠2=60°，且∠E=60°，
因此∠1=∠E，
∴，故③正确；
当时，则∠3+∠D=60°+30°=90°，
因此，故④正确，
故答案为：②③④．
【点睛】本题考查了三角板中角度的计算、平行线的判定及两直线垂直的判定，熟练掌握其相关判定及性质是解题的关键．
三、解答题
11．（2022·江苏常州·七年级期末）填写下列空格：
已知：如图，点E在AB上，且CE平分∠ACD，∠1=∠2．求证：ABCD．
证明：∵CE平分∠ACD（已知），
∴____________________（__________）．
∵∠1=∠2（已知），
∴∠1=_______（___________________）．
∴ ABCD（ ______________________ ）．
【答案】；角平分线定义；；等量代换；内错角相等，两直线平行
【分析】先利用角平分线定义得，从而可得出=，即可由平行线的判定定理得出结论．
【详解】解：CE平分（已知），
（ 角平分线定义 ）．
（已知），
= （等量代换）．
ABCD（内错角相等，两直线平行）．
故答案为：；角平分线定义；；等量代换；内错角相等，两直线平行．
【点睛】本题考查解增分线的定义，平行线的判定，熟练掌握平行线的判定的定理是解题的关键．
12．（2022·北京延庆·七年级期末）如图，∠B+∠BAD=180°，∠1=∠2． 求证：ABCD．请将下面的证明过程补充完整．
证明：
∵∠B+∠BAD=180°（已知），
∠1+∠BAD=180°（ ），
∴∠1=∠B（ ）．
∵∠1=∠2（已知），
∴∠2＝ （ ）．
∴ABCD（ ）．
【答案】见解析
【分析】根据平行的判定定理证明即可．
【详解】∵∠B+∠BAD=180°（已知），
∠1+∠BAD=180°（平角定义），
∴∠1=∠B（同角的补角相等）．
∵∠1=∠2（已知），
∴∠2=∠B（等量代换）．
∴ABCD（同位角相等，两条直线平行）．
【点睛】本题考查平行线的判定定理，解题的关键是掌握平行线的判定定理：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．
13．（2022·安徽·滁州市南谯区黄泥岗镇张浦郢中学八年级开学考试）完成下面的证明：
如图，BE平分∠ABD，DE平分∠BDC，且∠α+∠β＝90°，求证：AB∥CD．
证明：∵BE平分∠ABD （ ）
∴∠ABD＝2∠α （ ）
∵DE平分∠BDC（已知）
∵∠BDC＝ （ ）
∴∠ABD+∠BDC＝2∠α+2∠β＝2（∠α+∠β） （ ）
∵∠α+∠β＝90°（已知）
∴∠ABD+∠BDC＝（ ）
∴ AB∥CD （ ）
【答案】已知；角平分线的定义；2∠β ；角平分线的定义；等量代换；180°；同旁内角互补两直线平行
【分析】首先根据角平分线的定义可得∠ABD=2∠α，∠BDC=2∠β，根据等量代换可得∠ABD+∠BDC=2∠α+2∠β=2（∠α+∠β），进而得到∠ABD+∠BDC=180°，然后再根据同旁内角互补两直线平行可得答案．
【详解】解：∵BE平分∠ABD （已知），
∴∠ABD=2∠α（角平分线的定义）．
∵DE平分∠BDC（已知），
∴∠BDC=2∠β （角平分线的定义），
∴∠ABD+∠BDC=2∠α+2∠β=2（∠α+∠β）（等量代换），
∵∠α+∠β=90°（已知），
∴∠ABD+∠BDC=180°，
∴AB∥CD（同旁内角互补两直线平行）．
【点睛】此题主要考查了平行线的判定，关键是掌握角平分线定义和平行线的判定方法．
14．（2022·广东茂名·七年级阶段练习）如图，直线AF、DE，射线平分∠ABD交DE于点C．
(1)若∠DBF=54°，求∠2的度数；
(2)若．请说明：AB//CD．
【答案】(1)∠2=63°
(2)见解析
【分析】（1）根据∠DBF=54°，∠ABD+∠DBF=180°，得到∠ABD=126°，根据平分得到∠2=×126°=63°；
(2)根据平分，得到，根据，得到 ，推出．
（1）
（1）∵∠DBF=54°，∠ABD+∠DBF=180°
∴∠ABD=126°
∵平分
∴∠2=×126°=63°；
（2）
(2)∵平分
∴
∵
且
∴
∴．
【点睛】本题考查了邻补角性质，角平分线性质，对顶角性质，平行线的判定定理，熟练掌握邻补角的和等于180°，角平分线把一个角分成两个相等的角，对顶角相等，同旁内角互补两直线平行，是解决此题的关键．
15．（2022·黑龙江·大庆市高新区学校七年级期末）已知：如图，∠C=∠1，∠2和∠D互余，BE⊥FD于点G．
(1)填空：∠2和∠D可用关系式表示为______；∠1与∠D有怎样的关系式：______；
(2)求证：
【答案】(1)；
(2)见解析
【分析】（1）根据互余的定义及三角形内角和定理进行求解即可；
（2）根据同角的余角相等可得，继而证明，根据内错角相等，即可得到结论．
（1）
∠2和∠D互余，
；
BE⊥FD，
，
，
；
故答案为：；；
（2）
∠2和∠D互余，
，
BE⊥FD，
，
，
，
，
，
，
．
【点睛】本题考查了余角的定义，同角的余角相等及平行线的判定，熟练掌握知识点是解题的关键．
16．（2022·江苏·七年级）如图，点在直线上，射线、分别平分、．
(1)试判断、的位置关系，并说明理由；
(2)若，且，求证：．
【答案】(1)，理由见解析
(2)见解析
【分析】（1）根据角平分线定义以及平角的定义即可求证；
（2）由等角的余角相等可证得，进而可得，再由内错角相等两直线平行即可证得．
(1)
解：，
理由如下：
∵平分，平分，
∴，，
，
∴，
∴；
(2)
证明：∵（已证），（已知），
又∵，
∴，
∵，
∴，
∴．
【点睛】本题考查了角平分线定义，平角定义，平行线的判定，等角的余角相等，综合掌握以上知识并熟练应用是解题的关键．