初中数学浙教版七年级下册1.4平行线的性质课堂检测

这是一份初中数学浙教版七年级下册1.4平行线的性质课堂检测，共23页。
 浙教版七年级数学下册《1.4平行线的性质》解答题优生辅导训练（附答案）
1．如图，已知AD⊥BC，EF⊥BC，垂足分别为D、F，∠2+∠3＝180°，试说明：∠GDC＝∠B．请补充说明过程，并在括号内填上相应的理由．
解：∵AD⊥BC，EF⊥BC（已知）
∴∠ADB＝∠EFB＝90° （　 　），
∴EF∥AD（　 　），
∴　 　+∠2＝180°（　 　）．
又∵∠2+∠3＝180°（已知），
∴∠1＝∠3（　 　），
∴AB∥　 　（　 　），
∴∠GDC＝∠B（　 　）．

2．已知，如图，AD是△ABC的角平分线，DE∥AC，DE交AB于点E，DF∥AB，DF交AC于点F．
求证：DA平分∠EDF．

3．已知，如图，△ABC中，AB＞AC，AF是角平分线，D是AB上一点，且AD＝AC，DE∥BC交AC于E，求证：CD平分∠EDF．


4．如图，MN∥BC，BD⊥DC，∠1＝∠2＝60°，DC是∠NDE的平分线．
（1）AB与DE平行吗？请说明理由；
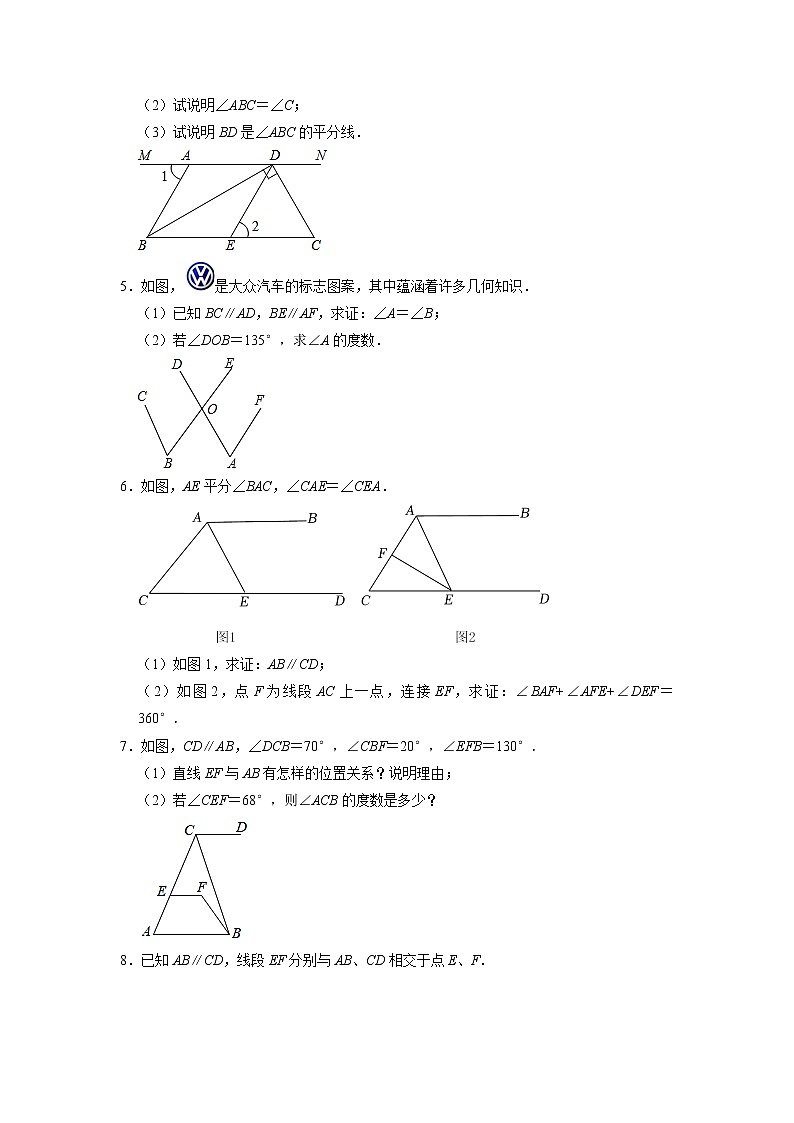
（2）试说明∠ABC＝∠C；
（3）试说明BD是∠ABC的平分线．

5．如图，是大众汽车的标志图案，其中蕴涵着许多几何知识．
（1）已知BC∥AD，BE∥AF，求证：∠A＝∠B；
（2）若∠DOB＝135°，求∠A的度数．

6．如图，AE平分∠BAC，∠CAE＝∠CEA．

（1）如图1，求证：AB∥CD；
（2）如图2，点F为线段AC上一点，连接EF，求证：∠BAF+∠AFE+∠DEF＝360°．
7．如图，CD∥AB，∠DCB＝70°，∠CBF＝20°，∠EFB＝130°．
（1）直线EF与AB有怎样的位置关系？说明理由；
（2）若∠CEF＝68°，则∠ACB的度数是多少？

8．已知AB∥CD，线段EF分别与AB、CD相交于点E、F．

（1）如图①，当∠A＝20°，∠APC＝70°时，求∠C的度数；
（2）如图②，当点P在线段EF上运动时（不包括E、F两点），∠A、∠APC与∠C之间有怎样的数量？试证明你的结论；
（3）如图③，当点P在直线EF上运动时，（2）中的结论还成立吗？如果成立，说明理由；如果不成立，直接写出它们之间的数量关系．
9．已知AB∥CD，点M为直线AC上的动点（点M不与点A，C重合），ME⊥AC交直线CD于E．
（1）如图1，当点M在CA上时，若∠MAB＝46°，则∠MEC＝　 　．
（2）如图2，当点M在CA的延长线上时，∠MAB与∠MEC有怎样的数量关系？写出结论，并说明理由．
（3）当点M在AC的延长线上时，∠MAB与∠MEC有怎样的数量关系？请直接写出结论．

10．（1）（问题）如图1，若AB∥CD，∠AEP＝40°，∠PFD＝130°．求∠EPF的度数；
（2）（问题迁移）如图2，AB∥CD，点P在AB的上方，问∠PEA，∠PFC，∠EPF之间有何数量关系？请说明理由；
（3）（联想拓展）如图3所示，在（2）的条件下，已知∠EPF＝α，∠PEA的平分线和∠PFC的平分线交于点G，用含有α的式子表示∠G的度数．

11．（1）如图（1），AB∥EF．求证：∠BCF＝∠B+∠F．
（2）当点C在直线BF的右侧时，如图（2），若AB∥EF，则∠BCF与∠B、∠F的关系如何？请说明理由．

12．已知：在四边形ABCD中，∠B＝∠D，点E在边BC的延长线上，连接AE交CD于点F，若∠BAF+∠AFC＝180°．
（1）如图1，求证：AD∥BC；
（2）如图2，过点D作DG∥AE交BE的延长线于点C，若∠G＝∠B，在不添加任何辅助线的情况下，请直接写出图2中除∠B以外的四个与∠G相等的角．



13．已知：如图，点B、C在线段AD的异侧，点E、F分别是线段AB、CD上的点，∠AEG＝∠AGE，∠C＝∠DGC．
（1）求证：AB∥CD；
（2）若∠AGE+∠AHF＝180°，求证：∠B＝∠C；
（3）在（2）的条件下，若∠BFC＝4∠C，求∠D的度数．

14．点E在射线DA上，点F、G为射线BC上两个动点，满足∠DBF＝∠DEF，∠BDG＝∠BGD，DG平分∠BDE．
（1）如图1，当点G在F右侧时，求证：BD∥EF；
（2）如图2，当点G在F左侧时，求证：∠DGE＝∠BDG+∠FEG；
（3）如图3，在（2）的条件下，P为BD延长线上一点，DM平分∠BDG，交BC于点M，DN平分∠PDM，交EF于点N，连接NG，若DG⊥NG，∠B﹣∠DNG＝∠EDN，则∠B的度数为 　 　．


15．已知AB∥CD，点E是AB，CD之间的一点．
（1）如图1，试探索∠AEC，∠BAE，∠DCE之间的数量关系；
以下是小明同学的探索过程，请你结合图形仔细阅读，并完成填空（理由或数学式）：
解：过点E作PE∥AB（过直线外一点有且只有一条直线与这条直线平行）．
∵AB∥CD（已知），
∴PE∥CD（ 　 　），
∴∠BAE＝∠1，∠DCE＝∠2（ 　 　），
∴∠BAE+∠DCE＝　 　+　 　（等式的性质）．
即∠AEC，∠BAE，∠DCE之间的数量关系是 　 　．
（2）如图2，点F是AB，CD之间的一点，AF平分∠BAE，CF平分∠DCE．
①若∠AEC＝74°，求∠AFC的大小；
②若CG⊥AF，垂足为点G，CE平分∠DCG，∠AEC+∠AFC＝126°，求∠BAE的大小．


16．已知一角的两边与另一个角的两边分别平行，试探索这两个角之间的关系，并说明你的结论．
（1）如图1所示，AB∥EF，BC∥DE，则∠1与∠2的关系是 　 　；
（2）如图2所示，AB∥EF，BC∥DE，则∠1与∠2的关系是 　 　；
（3）经过上述探索，我们可以得到一个结论（试用文字语言表述）：　 　；
（4）若两个角的两边分别平行，且一个角比另一个角的2倍少30°，则这两个分别是多少度？




17．已知：直线AB∥CD，一块三角板EFH，其中∠EFH＝90°，∠EHF＝60°．
（1）如图1，三角板EFH的顶点H落在直线CD上，并使EH与直线AB相交于点G，若∠2＝2∠1，求∠1的度数；
（2）如图2，当三角板EFH的顶点F落在直线AB上，且顶点H仍在直线CD上时，EF与直线CD相交于点M，试确定∠E、∠AFE、∠MHE的数量关系；
（3）如图3，当三角板EFH的顶点F落在直线AB上，顶点H在AB、CD之间，而顶点E恰好落在直线CD上时得△EFH，在线段EH上取点P，连接FP并延长交直线CD于点T，在线段EF上取点K，连接PK并延长交∠CEH的角平分线于点Q，若∠Q﹣∠HFT＝15°，且∠EFT＝∠ETF，求证：PQ∥FH．


18．点E在射线DA上，点F、G为射线BC上两个动点，满足∠DBF＝∠DEF，∠BDG＝∠BGD，DG平分∠BDE．
（1）如图1，当点G在F右侧时，求证：BD∥EF；
（2）如图2，当点G在BF左侧时，求证：∠DGE＝∠BDG+∠FEG；
（3）如图3，在（2）的条件下，P为BD延长线上一点，DM平分∠BDG，交BC于点M，DN平分∠PDM，交EF于点N，连接NG，若DG⊥NG，∠B﹣∠DNG＝∠EDN，求∠B的度数．


19．已知两条直线l1，l2，l1∥l2，点A，B在直线l1上，点A在点B的左边，点C，D在直线l2上，且满足∠ADC＝∠ABC＝115°．

（1）如图①，求证：AD∥BC；
（2）点M，N在线段CD上，点M在点N的左边且满足∠MAC＝∠BAC，且AN平分∠CAD；
（Ⅰ）如图②，当∠ACD＝30°时，求∠DAM的度数；
（Ⅱ）如图③，当∠CAD＝8∠MAN时，求∠ACD的度数．

20．图1展示了光线反射定律：EF是镜面AB的垂线，一束光线m射到平面镜AB上，被AB反射后的光线为n，则入射光线m，反射光线n与垂线EF所夹的锐角θ1＝θ2．
（1）在图1中，证明：∠1＝∠2．
（2）图2中，AB，BC是平面镜，入射光线m经过两次反射后得到反射光线n，已知∠1＝30°，∠4＝60°，判断直线m与直线n的位置关系，并说明理由．
（3）图3是潜望镜工作原理示意图，AB，CD是平行放置的两面平面镜．请解释进入潜望镜的光线m为什么和离开潜望镜的光线n是平行的？


参考答案
1．解：∵AD⊥BC，EF⊥BC（已知）
∴∠ADB＝∠EFB＝90°（垂直的定义），
∴EF∥AD （同位角相等两直线平行），
∴∠1+∠2＝180°（两直线平行同旁内角互补），
又∵∠2+∠3＝180°（已知），
∴∠1＝∠3 （同角的补角相等），
∴AB∥DG（内错角相等两直线平行），
∴∠GDC＝∠B （两直线平行同位角相等）．
故答案为：垂直的定义，同位角相等两直线平行，∠1，两直线平行同旁内角互补，同角的补角相等，DG，内错角相等两直线平行，两直线平行同位角相等．
2．证明：∵DE∥AC，DF∥AB，
∴∠DAF＝∠ADE，∠DAE＝∠ADF．
∵AD是△ABC的角平分线，
∴∠DAF＝∠DAE．
∴∠ADE＝∠ADF．
∴DA平分∠EDF．
3．证明：∵AD＝AC，AF是角平分线，
∴AF垂直平分CD，
∴CF＝DF，
∴∠FDC＝∠FCD，
∵DE∥BC，
∴∠EDC＝∠DCF，
∴∠EDC＝∠FDC，
∴CD平分∠DEF．
4．解：（1）AB∥DE，理由如下：
∵MN∥BC，（ 已知 ）
∴∠ABC＝∠1＝60°．（ 两直线平行，内错角相等 ）
又∵∠1＝∠2，（ 已知 ）
∴∠ABC＝∠2．（ 等量代换 ）
∴AB∥DE．（ 同位角相等，两直线平行 ）；
（2）∵MN∥BC，
∴∠NDE+∠2＝180°，
∴∠NDE＝180°﹣∠2＝180°﹣60°＝120°．
∵DC是∠NDE的平分线，
∴∠EDC＝∠NDC＝∠NDE＝60°．
∵MN∥BC，
∴∠C＝∠NDC＝60°．
∴∠ABC＝∠C．
（3）∠ADC＝180°﹣∠NDC＝180°﹣60°＝120°，
∵BD⊥DC，
∴∠BDC＝90°．
∴∠ADB＝∠ADC﹣∠BDC＝120°﹣90°＝30°．
∵MN∥BC，
∴∠DBC＝∠ADB＝30°．
∴∠ABD＝∠DBC＝∠ABC．
∴BD是∠ABC的平分线．
5．（1）证明：∵BC∥AD，
∴∠B＝∠DOE，
又∵BE∥AF，
∴∠DOE＝∠A，
∴∠A＝∠B．
（2）解：∵BE∥AF，
∴∠EOA+∠A＝180°，
∵∠EOA＝∠DOB＝135°，
∴∠A＝180°﹣∠EOA＝180°﹣135°＝45°．
6．证明：（1）∵AE平分∠BAC，
∴∠BAE＝∠CAE，
∵∠CAE＝∠CEA，
∴∠CEA＝∠BAE，
∴AB∥CD；
（2）过F作FM∥AB，如图，

∵AB∥CD，
∴AB∥FM∥CD，
∴∠BAF+∠AFM＝180°，∠DEF+∠EFM＝180°，
∴∠BAF+∠AFM+∠DEF+∠EFM＝360°，
即∠BAF+∠AFE+∠DEF＝360°．
7．解：（1）EF和AB的位置关系为平行关系．理由如下：
∵CD∥AB，∠DCB＝70°，
∴∠DCB＝∠ABC＝70°，
∵∠CBF＝20°，
∴∠ABF＝∠ABC﹣∠CBF＝50°，
∵∠EFB＝130°，
∴∠ABF+∠EFB＝50°+130°＝180°，
∴EF∥AB；
（2）∵EF∥AB，CD∥AB，
∴EF∥CD，
∵∠CEF＝68°，
∴∠ECD＝112°，
∵∠DCB＝70°，
∴∠ACB＝∠ECD﹣∠DCB，
∴∠ACB＝42°．
8．（1）解：过P作PO∥AB，

∵AB∥CD，
∴AB∥PO∥CD，
∵∠A＝20°，当点P在线段EF上运动时，
∴∠APO＝∠A＝20°，∠C＝∠CPO，
∵∠APC＝70°，
∴∠C＝∠CPO＝∠APC﹣∠APO＝70°﹣20°＝50°；
（2）∠A+∠C＝∠APC，
证明：过P作PO∥AB，

∵AB∥CD，
∴AB∥PO∥CD，
∴∠APO＝∠A，∠C＝∠CPO，
∴∠APC＝∠APO+∠CPO＝∠A+∠C；
（3）解：①当P在线段EF的延长线上运动时，不成立，关系式是：∠A﹣∠C＝∠APC，
理由是：过P作PO∥AB，

∵AB∥CD，
∴AB∥PO∥CD，
∴∠APO＝∠A，∠C＝∠CPO，
∴∠A﹣∠C＝∠APO﹣∠CPO＝∠APC，
即∠A﹣∠C＝∠APC；
②当点P在线段FE的延长线上运动时，新的相等关系为∠C＝∠APC+∠A．
理由：设AB与CP相交于Q，则∠PQB＝∠APC+∠A．

∵AB∥CD，
∴∠C＝∠PQB，
∴∠C＝∠APC+∠A．
③当点P在线段EF上运动时，成立，关系式为∠A+∠C＝∠APC，
证明：过P作PO∥AB，

∵AB∥CD，
∴AB∥PO∥CD，
∴∠APO＝∠A，∠C＝∠CPO，
∴∠APC＝∠APO+∠CPO＝∠A+∠C；
综上所述，当点P在直线EF上运动时，（2）中的结论不一定成立．
9．解：（1）∵AB∥CD，∠MAB＝46°，
∴∠ACE＝∠MAB＝46°，
∵ME⊥AC交直线CD于E，
∴∠CME＝90°，
∴∠MEC＝90°﹣∠MCE＝44°．
故答案为：44°；
（2）∠MAB＝90°+∠MEC，理由如下：
∵ME⊥AC交直线CD于E．
∴∠CME＝90°，
∴∠MCE＝90°﹣∠MEC，
∵AB∥CD，
∴∠BAC＝∠MCE＝90°﹣∠MEC，
∵∠MAB＝180°﹣∠BAC，
∴∠MAB＝180°﹣（90°﹣∠MEC）＝90°+∠MEC；
（3）∴∠MEC+∠BAC＝90°，理由如下：
如图所示：

∵AB∥CD，
∴∠BAC＝∠MCE，
∵ME⊥AC交直线CD于E，
∴∠CME＝90°，
∴∠MEC＝90°﹣∠MCE＝90°﹣∠BAC，
∴∠MEC+∠BAC＝90°．
10．解：（1）如图1，过点P作PM∥AB，

∴∠1＝∠AEP＝40°．（两直线平行，内错角相等）
∵AB∥CD，（已知）
∴PM∥CD，（平行于同一条直线的两直线平行）
∴∠2+∠PFD＝180°． （两直线平行，同旁内角互补）
∵∠PFD＝130°，
∴∠2＝180°﹣130°＝50°．
∴∠1+∠2＝40°+50°＝90°．
即∠EPF＝90°．
（2）∠PFC＝∠PEA+∠P．
理由：如图2，过P点作PN∥AB，则PN∥CD，

∴∠PEA＝∠NPE，
∵∠FPN＝∠NPE+∠FPE，
∴∠FPN＝∠PEA+∠FPE，
∵PN∥CD，
∴∠FPN＝∠PFC，
∴∠PFC＝∠PEA+∠FPE，即∠PFC＝∠PEA+∠P；
（3）如图，过点G作AB的平行线GH．

∵GH∥AB，AB∥CD，
∴GH∥AB∥CD，
∴∠HGE＝∠AEG，∠HGF＝∠CFG，
又∵∠PEA的平分线和∠PFC的平分线交于点G，
∴∠HGE＝∠AEG＝，∠HGF＝∠CFG＝，
由（1）可知，∠CFP＝∠P+∠AEP，
∴∠HGF＝（∠P+∠AEP）＝（α+∠AEP），
∴∠EGF＝∠HGF﹣∠HGE＝（α+∠AEP）＝+∠AEP﹣∠HGE＝．
11．（1）证明：过C作CD∥AB，
∵AB∥EF，
∴CD∥AB∥EF，
∴∠B＝∠BCD，∠F＝∠FCD，
∴∠B+∠F＝∠BCF．
（2）∠B+∠F+∠BCF＝360°，
理由是：过C作CD∥AB，
则∠B+∠BCD＝180°，
又∵AB∥EF，AB∥CD，
∴CD∥EF∥AB，
∴∠F+∠FCD＝180°，
∴∠B+∠F+∠BCF＝360°．
12．（1）证明：∵∠BAF+∠AFC＝180°，
∴AB∥CD，
∴∠B＝∠ECD，
∵∠B＝∠D，
∴∠D＝∠ECD，
∴AD∥BC；
（2）∵DG∥AE，
∴∠G＝∠AEB，
由（1）得AD∥BC，
∴∠AEB＝∠DAE，∠ADC＝∠DCG，
∴∠G＝∠DAE，
∵∠B＝∠ADC，∠G＝∠B，
∴∠G＝∠ADC＝∠DCG，
综上所述，所∠G相等的角有：∠AEB，∠DAE，∠ADC，∠DCG．
13．（1）证明：∵∠AEG＝∠AGE，∠C＝∠DGC，∠AGE＝∠DGC，
∴∠AEG＝∠C，
∴AB∥CD；
（2）证明：∵∠AGE+∠EGH＝180°，∠AGE+∠AHF＝180°，
∴∠EGH＝∠AHF，
∴EC∥BF，
∴∠B＝∠AEG，
∵AB∥CD，
∴∠C＝∠AEG，
∴∠B＝∠C；
（3）解：∵BF∥EC，
∴∠C+∠BFC＝180°，
∵∠BFC＝4∠C，
∴∠C+4∠C＝180°，
解得∠C＝36°，
∵∠C＝∠DGC，
∴∠DGC＝36°，
∴∠D＝180°﹣∠C﹣∠DGC＝108°．
14．证明：（1）∵DG平分∠BDE，
∴∠BDG＝∠ADG．
又∵∠BDG＝∠BGD，
∴∠ADG＝∠DGB．
∴AD∥BC．
∴∠DEF＝∠EFG．
∵∠DBF＝∠DEF，
∴∠DBF＝∠EFG．
∴BD∥EF．
（2）过点G作GH∥BD，交AD于点H，如图，

∵BD∥EF，
∴GH∥EF．
∴∠BDG＝∠DGH，∠GEF＝∠HGE，
∵∠DGE＝∠DGH+∠HGE，
∴∠DGE＝∠BDG+∠FEG．
（3）设∠BDM＝∠MDG＝α，
则∠BDG＝∠EDG＝∠DGB＝2α，∠PDE＝180°﹣4α．
∴∠PDM＝180°﹣α．
∵DN平分∠PDM，
∴．
∴∠EDN＝∠PDN−∠PDE＝90°﹣﹣（180°﹣4α）＝﹣90°．
∴∠GDN＝∠MDN﹣∠MDG＝90°﹣﹣α＝90°﹣．
∵DG⊥ON，
∴∠DNG＝90°．
∴∠DNG＝90°−（90°−）＝．
∵DE∥BF，
∴∠B＝∠PDE＝180°﹣4α．
∵∠B﹣∠DNG＝∠EDN，
∴180°−4α−＝﹣90°，
解得：α＝30°．
∴∠B＝180°﹣4α＝60°，
故答案为：60°．
15．解：（1）平行于同一条直线的两条直线平行，
两直线平行，内错角相等，
∠1，∠2，
∠AEC＝∠BAE+∠DCE，
故答案为：平行于同一条直线的两条直线平行，
两直线平行，内错角相等，
∠1，∠2，
∠AEC＝∠BAE+∠DCE，
（2）①由（1）得：
∠AEC＝∠BAE+∠DCE，
∠AFC＝∠BAF+∠DCF，
∵AF平分∠BAE，CF平分∠DCE，
∴∠BAF＝∠BAE，∠DCF＝∠DCE，
∴∠AFC＝∠BAF+∠DCF
＝∠BAE+∠DCE
＝∠AEC
＝×74°
＝37°；
②由①得：∠AEC＝2∠AFC，
∵∠AEC+∠AFC＝126°，
∴∠AFC＝42°，∠AEC＝82°，
∵CG⊥AF，
∴∠CGF＝90°，
∴∠GCF＝48°，
∵CE平分∠DCG，
∴∠GCE＝∠ECD，
∵CF平分∠DCE，
∴∠DCE＝2∠DCF＝2∠ECF，
∴∠GCF＝3∠DCF，
∴∠DCF＝16°，
∴∠DCE＝32°，
∴∠BAE＝∠AEC﹣∠DCE＝52°．

16．解：（1）如图1．

∵AB∥EF，
∴∠1＝∠3．
∵BC∥DE，
∴∠3＝∠2．
∴∠1＝∠2．
故答案为：∠1＝∠2．
（2）∵AB∥EF，
∴∠1＝∠BGE．
∵BC∥DE，
∴∠2+∠BGE＝180°．
∴∠1+∠2＝180°．
故答案为：∠1+∠2＝180°．
（3）由（1）、（2）得：一角的两边与另一个角的两边分别平行，则这两个角要么相等，要么互补．
（4）这这两个角分别是∠1、∠2，且∠1＝2∠2﹣30°．
∵∠1+∠2＝180°，
∴2∠2﹣30°+∠2＝180°．
∴∠2＝70°．
∴∠1＝2×70°﹣30°＝110°．
∴这两个角分别为70°、110°．
17．（1）解：∵AB∥CD，
∴∠1＝∠CHG．
∵∠2＝2∠1，
∴∠2＝2∠CHG．
∵∠CHG+∠EHF+∠2＝180°，
∴3∠CHG+60°＝180°．
∴∠CHG＝40°．
∴∠1＝40°．
（2）解：∠E、∠AFE、∠MHE的数量关系为：∠AFE＝∠E+∠MHE，理由：
∵AB∥CD，
∴∠AFE＝∠CME．
∵∠CME＝∠E+∠MHE，
∴∠AFE＝∠E+∠MHE．
（3）证明：设∠AFE＝x，则∠BFH＝90°﹣x，∠EFB＝180°﹣x．
∵AB∥CD，
∴∠BFT＝∠ETF．
∵∠EFT＝∠ETF，
∴∠EFT＝∠BFT＝∠EFB＝90°﹣x．
∴∠HFT＝∠BFT﹣∠BFH＝x．
∵∠Q﹣∠HFT＝15°，
∴∠Q＝15°+x．
∵AB∥CD，
∴∠AFE+∠CEF＝180°．
∴∠CEF＝180°﹣x．
∴∠CEH＝∠CEF+∠FEH＝180°﹣x+30°＝210°﹣x．
∵EQ平分∠CEH，
∴∠QEH＝∠CEH＝105°﹣x．
∵∠Q+∠QEH+∠QPE＝180°，
∴15°+x+105°﹣x+∠QPE＝180°．
∴∠QPE＝60°．
∵∠H＝60°，
∴∠QPE＝∠H．
∴PQ∥FH．
18．证明：（1）∵DG平分∠BDE，
∴∠BDG＝∠ADG．
又∵∠BDG＝∠BGD，
∴∠ADG＝∠DGB．
∴AD∥BC．
∴∠DEF＝∠EFG．
∵∠DBF＝∠DEF，
∴∠DBF＝∠EFG．
∴BD∥EF．
（2）过点G作GH∥BD，交AD于点H，如图，

∵BD∥EF，
∴GH∥EF．
∴∠BDG＝∠DGH，∠GEF＝∠HGE，
∵∠DGE＝∠DGH+∠HGE，
∴∠DGE＝∠BDG+∠FEG．
（3）设∠BDM＝∠MDG＝α，
则∠BDG＝∠EDG＝∠DGB＝2α，∠PDE＝180°﹣4α．
∴∠PDM＝180°﹣α．
∵DN平分∠PDM
∴．
∴．
∴∠GDN＝∠MDN﹣∠MDG＝90°﹣﹣α＝90°﹣．
∵DG⊥ON，
∴∠DNG＝90°．
∴．

∵DE∥BF，
∴∠B＝∠PDE＝180°﹣4α．
∵∠B﹣∠DNG＝∠EDN，
∴，
解得：α＝30°．
∴∠B＝180°﹣4α＝60°．
19．证明：（1）∵l1∥l2，
∴∠ABC+∠BCD＝180°．
∵∠ADC＝∠ABC，
∴∠ADC+∠BCD＝180°．
∴AD∥BC．
解：（2）（Ⅰ）∵l1∥l2，
∴∠BAC＝∠ACD＝30°．
∵∠MAC＝∠BAC，
∴∠MAC＝30°．
∵∠ADC＝∠ABC＝115°，∠ACD＝30°，
∴∠DAC＝180°﹣∠ADC﹣∠ACD＝35°．
∴∠DAM＝∠DAC﹣∠MAC＝35°﹣30°＝5°．
（Ⅱ）设∠MAN＝x°，则∠CAD＝8x°，
∵AN平分∠CAD，
∴∠DAN＝∠CAN＝4x°．
∴∠CAM＝∠MAN+∠CAN＝5x°．
∵∠DAB＝180°﹣∠ADC＝65°，
∴∠CAB＝∠DAB﹣∠DAC＝65°﹣8x°，
∵l1∥l2，
∴∠DCA＝∠CAB＝65°﹣8x°．
∴65°﹣8x°＝5x°．
解得：x＝5．
∴∠ACD＝5x＝25°．
20．（1）证明：∵∠AFE＝∠BFE＝90°，
∵θ1＝θ2．
∴∠1＝∠2；
（2）解：直线m∥直线n，
理由：如图2，∵∠1＝∠2＝30°，∠3＝∠4＝60°，
∴∠5＝180°﹣∠1﹣∠2＝120°，∠6＝180°﹣∠3﹣∠4＝60°，
∴∠5+∠6＝180°，
∴直线m∥直线n；
（3）解：∵AB∥CD，
∴∠2＝∠3，
∵∠1＝∠2，∠3＝∠4，
∴∠1＝∠2＝∠3＝∠4，
∴180°﹣∠1﹣∠2＝180°﹣∠3﹣∠4，
即：∠5＝∠6，
∴m∥n．