






中考数学优化探究一轮复习(理数) 第6章 第2节 二元一次不等式(组)与简单的线性规划问题课件PPT
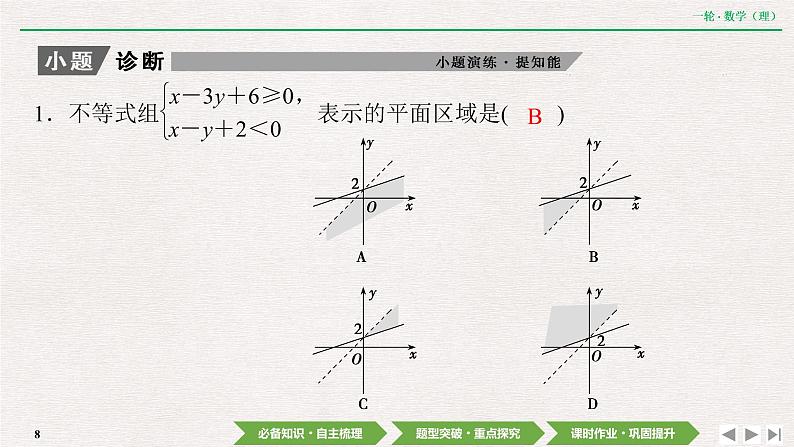
展开第六章 不等式第二节 二元一次不等式(组)与简单的线性规划问题
知识点 简单的线性规划1.二元一次不等式(组)表示的平面区域
2.线性规划中的基本概念
1.画平面区域时避免失误的重要方法就是首先使二元一次不等式化为Ax+By+C>0(A>0)的形式.2.线性规划问题中的最优解不一定是唯一的,即可行域内使目标函数取得最值的点不一定只有一个,也可能有无数多个,也可能没有.
解析:先根据约束条件画出可行域,如图中阴影部分所示,当直线z=ax+y和直线AB重合时,z取得最大值的点(x,y)有无数个,所以-a=kAB=1,所以a=-1.
3.投资生产A产品时,每生产100吨需要资金200万元,需场地200平方米;投资生产B产品时,每生产100吨需要资金300万元,需场地100平方米.现某单位可使用资金1 400万元,场地900平方米,则上述要求可用不等式组表示为_________________.(用x,y分别表示生产A,B产品的吨数,x和y的单位是百吨)
解析:用表格列出各数据
所以不难看出,x≥0,y≥0,200x+300y≤1 400,200x+100y≤900.
题型一 二元一次不等式(组)表示的平面区域
解析:由于x=1与x+y-4=0不可能垂直,所以只有可能x+y-4=0与kx-y=0垂直或x=1与kx-y=0垂直.①当x+y-4=0与kx-y=0垂直时,k=1,检验知三角形区域面积为1,即符合要求;②当x=1与kx-y=0垂直时,k=0,检验不符合要求.综上,实数k的值为1.
根据平面区域确定参数的方法在含有参数的二元一次不等式组所表示的平面区域问题中,首先把不含参数的平面区域确定好,然后用数形结合的方法根据参数的不同取值情况画图观察区域的形状,根据求解要求确定问题的答案.
题型二 目标函数的最值及应用
线性规划问题是高考的重点,而线性规划问题具有代数和几何的双重形式,多与函数、平面向量、数列、三角函数、概率、解析几何等问题交叉渗透,自然地融合在一起,使数学问题的解答变得更加新颖别致.归纳起来常见的命题探究角度有:(1)求线性目标函数的最值;(2)求非线性目标函数的最值;(3)求目标函数中的参数;(4)线性规划的实际应用.
求目标函数最值的三步骤(1)作图——画出约束条件所确定的平面区域和目标函数所表示的平行直线系中过原点的那一条直线.(2)平移——将l平行移动,以确定最优解的对应点的位置.(3)求值——解方程组求出对应点坐标(即最优解),代入目标函数,即可求出最值.
[解析] (1)在坐标平面上点(x,y)所表示的区域如图所示,根据几何意义,u的值即为区域内的点与坐标原点连线的斜率,显然kOA最小,kOB最大.
求解线性规划中含参数问题的基本方法(1)把参数当成常数用,根据线性规划问题的求解方法求出最优解,代入目标函数确定最值,通过构造方程或不等式求解参数的值或取值范围.(2)先分离含有参数的式子,通过观察的方法确定含参的式子所满足的条件,确定最优解的位置,从而求出参数.
考法(四) 线性规划的实际应用[例4] 为了活跃学生课余生活,我校高三年级部计划使用不超过1 200元的资金购买单价分别为90元、120元的排球和篮球.根据需要,排球至少买3个,篮球至少买2个,并且排球的数量不得超过篮球数量的2倍,则能买排球和篮球的个数之和的最大值是________.
解答线性规划实际问题的三步骤(1)根据题意设出变量,找出约束条件和目标函数.(2)准确作出可行域,求出最优解.(3)将求解出来的结论反馈到实际问题当中,设计最佳方案.
3.某届冬奥会中国运动健儿发挥稳定,向世界展现了良好的精神风貌.在饮食方面,每天的中餐主办方向运动员提供A和B两种套餐.已知一个单位的A套餐含有6个单位的蛋白质、6个单位的碳水化合物和12个单位的维生素;一个单位的B套餐含有12个单位的蛋白质、6个单位的碳水化合物和6个单位的维生素.另外,营养师分析:一位运动员每天的中餐需要的营养中至少含有60个单位的蛋白质、42个单位的碳水化合物、54个单位的维生素.若每单位A,B套餐所需费用分别为4元和3元,则在满足上述营养的要求下,每位运动员每天的中餐至少花费_________元.
线性规划应用中的核心素养
求解此类问题的关键是利用转化思想与数形结合思想进行求解.
解析:因为a=(y-2x,m),b=(1,-1),a∥b,所以m=2x-y,作出可行域如图中阴影部分所示,作出直线2x-y=0,并平移,结合图像易知,m=2x-y取得最大值的最优解为(4,2),所以m的最大值为6.
中考数学优化探究一轮复习(理数) 第5章 第4节 数列求和课件PPT: 这是一份中考数学优化探究一轮复习(理数) 第5章 第4节 数列求和课件PPT,共40页。PPT课件主要包含了na1等内容,欢迎下载使用。
中考数学优化探究一轮复习(理数) 第8章 第9节 第2课时 最值、范围、证明问题课件PPT: 这是一份中考数学优化探究一轮复习(理数) 第8章 第9节 第2课时 最值、范围、证明问题课件PPT,共33页。
中考数学优化探究一轮复习(理数) 第8章 第5节 椭圆课件PPT: 这是一份中考数学优化探究一轮复习(理数) 第8章 第5节 椭圆课件PPT,共46页。PPT课件主要包含了等于常数,-aa,-bb,坐标轴,-a0,0-b,0-a,-b0,a2-b2等内容,欢迎下载使用。












