第03讲 复数（原卷版+解析版）-2023年高考数学必考考点二轮复习讲义（新高考专用）

这是一份第03讲 复数（原卷版+解析版）-2023年高考数学必考考点二轮复习讲义（新高考专用），文件包含第三讲复数讲义解析版docx、第三讲复数讲义原卷版docx等2份教案配套教学资源，其中教案共24页， 欢迎下载使用。
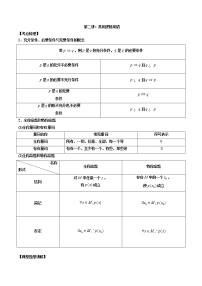
1、复数的有关概念
（1）形如 ()的数叫做复数，其中 分别是复数的实部和虚部．若 ，则 为实数；若 ，则 为虚数；若 且 ，则 为纯虚数．
(2)复数相等：()．
(3)的共轭复数为 ()．
(4)复数()与复平面的点一一对应．
(5)复数()的模
注意：任意两个复数全是实数时能比较大小，其他情况不能比较大小．
2、复平面及复数的几何意义
（1）.复平面
（2）复数的几何意义
①复数()复平面内的点.
②复数()平面向量.
（3）复数的模：①定义：向量的模叫做复数()的模或绝对值.
②记法：复数i的模记为或 ③公式：
（3）共轭复数：当两个复数的实部相等，虚部互为相反数时，这两个复数叫做互为共轭复数.虚部不等于0的两个共轭复数也叫共轭虚数.
2.表示：的共轭复数用表示，即若()，则
3、复数加法与减法的运算法则
（1）设，()是任意两个复数，则
①；②
（2）对任意，有
①；②.
4、复数加减法的几何意义
如图，设复数，对应向量分别为，，四边形为平行四边形，向量与复数对应，向量eq \(Z2Z1,\s\up6(→))与复数对应.
5、复数乘法的运算法则和运算律
（1）复数的乘法法则
设，()是任意两个复数，则.
2.复数乘法的运算律
对任意复数，有
6、复数除法的法则
设，(，且)是任意两个复数，
则
7、方程的虚数根
对所有的实系数一元二次方程，若，则此方程没有实根，但有两个虚根，且两根，故实系数方程的虚根成对出现．
8、常用结论
①②③
【典型题型讲解】
考点一：复数的相关概念
【典例例题】
例1.已知为复数，有以下四个命题，其中真命题的序号是（ ）
①若，则； ②若，则；
③若，则； ④若是虚数，则都是虚数.
A．①④B．②C．②③D．①②③
例2.已知，（，为虚数单位），则实数的值为（ ）
A．5B．6C．7D．8
【方法技巧与总结】
复数模、共轭复数、复数相等或代数运算都要认清复数包括实部和虚部两部分，所以在解决复数有关问题时要将复数的实部和虚部都认识清楚．
【变式训练】
1.已知复数和，则“”是“”的（ ）
A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件
2.已知，若复数是纯虚数，则（ ）
A．0B．2C．0或D．
3.若，则是的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分又不必要条件
考点二：复数的运算
【典例例题】
例1．（2022·广东·金山中学高三期末）（多选）下面是关于复数（为虚数单位）的命题，其中真命题为（ ）
A．B．
C．的共轭复数为D．的虚部为
例2．（2022·广东东莞·高三期末）（多选）已知复数，是的共轭复数，则下列结论正确的是（ ）
A．若，则B．若，则
C．若，则D．若，则
【方法技巧与总结】
设，则
（1）（2）
（3）
【变式训练】
1．（2022·广东汕尾·高三期末）若复数z满足其中（i为虚数单位），则复数z的共轭复数为（ ）
A．B．C．D．
2．（2022·广东清远·高三期末）已知i为虚数单位，复数z的共轭复数满足，则（ ）
A．B．C．D．
3．（2021·广东汕头·高三期末）已知i为虚数单位，复数z满足：z(1-i)=4-3i，则z=（ ）
A．B．C．D．
4.复数（ ）
A．B．C．D．
5.已知复数（为虚数单位）为实系数方程的一根，则（ ）
A．4B．2C．0D．
6．若 （为虚数单位），则（ ）
A．B．C．D．
7．若复数的虚部小于0，，且，则（ ）
A．B．C．D．
考点三：复数的几何意义
【典例例题】
例1.复数满足，则复数在复平面内所对应的点在（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
例2．（2022·全国·模拟预测）如图，在复平面内，复数，对应的向量分别是，，则对应的点位于（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
【方法技巧与总结】
复数的几何意义在于复数的实质是复平面上的点，其实部、虚部分别是该点的横坐标、纵坐标，这是研究复数几何意义的最重要的出发点．
【变式训练】
1．在复平面内，复数对应的点位于（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
2．已知为虚数单位，复数满足，则复数在复平面内对应的点位于（ ）
A． 第一象限 B． 第二象限 C． 第三象限 D． 第四象限
3．若复数在复平面内对应的点位于实轴上，则（ ）
A．4B．2C．D．
4．已知复数，则的共轭复数在复平面中对应的点在第（ ）象限
A．一B．二C．三D．四
5．在复平面内，复数对应的点的坐标为，则（ ）
A．B．C．D．
6．已知复数（为虚数单位）在复平面内对应的点在第三象限，则实数的取值范围是（ ）
A．B．C．D．
7．已知复数z满足，若复数z在复平面上对应的点在第二或第四象限，则实数a的取值范围是（ ）
A．B．
C．D．
【巩固练习】
一、单选题
1．已知复数，则的虚部为（ ）
A．B．C．D．
2．已知复数，则的共轭复数的虚部为（ ）
A．B．C．D．
3．已知，且，其中，为实数，则（ ）
A．1B．3C．D．5
4．复数z满足，则（ ）
A．1B．2C．D．3
5．已知为虚数单位，则复数对应的点位于（ ）
A．第一象限B．第二象限C．第三象限D．第四象限
6．已知复数z满足，则（ ）．
A．5B．C．22D．2
7．已知复数满足，若为纯虚数，则（ ）
A．B．1C．D．2
8．复平面内表示复数，则（ ）
A．B．C．4D．
9．欧拉公式（其中，为虚数单位）是由瑞士著名数学家欧拉创立，该公式建立了三角函数与指数函数的关系，在复变函数论中占有非常重要的地位，被誉为“数学中的天桥”根据欧拉公式，下列结论中正确的是（ ）
A．的实部为B．在复平面内对应的点在第一象限
C．D．的共轭复数为
二、多选题
10．（2022·河北·高三阶段练习）若复数z在复平面对应的点为Z，则下列说法正确的有（ ）
A．若，则
B．若，则Z在复平面内的轨迹为圆
C．若，满足，则的取值范围为
D．若，则的取值范围为
11．（2022·江苏·姜堰中学高三阶段练习）已知复数，则下列说法正确的是（ ）
A．复数在复平面内对应的点在第四象限B．复数的虚部为
C．复数的共轭复数D．复数的模
三、填空题
12．己知，则___________．
13．若复数为纯虚数，则___________.
14．如图，在复平面内，复数对应的向量分别是，若，则复数___________.
15．设为实数，复数，（其中i为虚数单位），若为纯虚数，则的值为_______.
交换律
结合律
乘法对加法的分配律