第12讲 三角恒等变换（原卷版+解析版）-2023年高考数学必考考点二轮复习讲义（新高考专用）

这是一份第12讲 三角恒等变换（原卷版+解析版）-2023年高考数学必考考点二轮复习讲义（新高考专用），文件包含第十二讲三角恒等变换解析版docx、第十二讲三角恒等变换原卷版docx等2份教案配套教学资源，其中教案共24页， 欢迎下载使用。
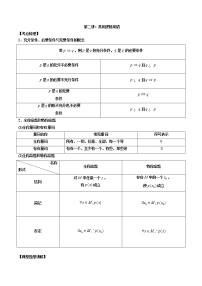
两角和与差的三角函数公式



二倍角公式


3、辅助角公式
(其中)
4、降幂公式

【典型题型讲解】
考点一：两角和与差公式
【典例例题】
例1．（2022·广东汕头·高三期末）已知，则（ ）
A．-1B．0C．D．
【答案】B
【详解】∵，∴，故
故选：B
例2.（2022·广东湛江·一模）已知，，则（ ）
B．C．D．
【答案】B
【详解】由，，得，
所以，
故选:B.
例3．（2022·广东汕头·一模）已知，，则（ ）
A．B．C．3D．
【答案】B
【详解】由，得，又，
得，即，
整理，得或(舍去)，
所以，又，，
解得，
故
.
故选：B
【方法技巧与总结】
1.三角函数式化简的方法：化简三角函数式常见方法有弦切互化，异名化同名，异角化同角，降幂与升幂等.
2.给值求值：解题的关键在于“变角”，把待求三角函数值的角用含已知角的式子表示出来，求解时要注意对角的范围的讨论.
【变式训练】
1.已知，则__________．
【答案】
【解析】本题主要考查三角恒等变换，考查考生的运算求解能力.
，解方程得.故答案为.
2.（2022·广东韶关·一模）若，则__________.
【答案】
【详解】因为，所以，所以，所以.
故答案为：
3.（2022·全国·高考真题）若，则（ ）
A．B．
C．D．
【答案】C
【详解】
由已知得：,
即：，
即：,
所以,
故选：C
4.已知，，且，，则（ ）
A．B．C．D．
【答案】A
【解析】
易知，利用角的范围和同角三角函数关系可求得和，分别在和两种情况下，利用两角和差正弦公式求得，结合的范围可确定最终结果.
【详解】
且，，.
又，，.
当时，
，
，，不合题意，舍去；
当，同理可求得，符合题意.
综上所述：.
故选：.
5.已知，则的值为（ ）
A．B．C．D．
【答案】A
【解析】
根据题意得到进而得到，，从而有.
【详解】
∵，
∴，
则，
，
∴
，
故选A.
考点二：二倍角公式
【典例例题】
例1.（2022·广东中山·高三期末）若，则___________.
【答案】
【分析】根据余弦的二倍角公式即可计算.
【详解】.
故答案为：.
例2．（2022·广东清远·高三期末）已知，则________．
答案】
【详解】
．
故答案为：
例3.若，则（ ）
A．B．C．D．
【答案】A
【详解】
，
，，，解得，
，.
故选：A.
【方法技巧与总结】
三角恒等变换的基本思路：找差异，化同角(名)，化简求值.三角恒等变换的关键在于观察各个角之间的联系，发现题目所给条件与恒等变换公式的联系.
【变式训练】
1．（2022·广东汕头·一模）已知，，则（ ）
A．B．C．3D．
【答案】．B
【详解】由，得，又，
得，即，
整理，得或(舍去)，
所以，又，，
解得，
故
.
故选：B
2．（2022·广东韶关·二模）已知 ，则（ ）
A．B．C．D．
【答案】．C
【详解】由题知，有，
所以，
故选：C．
3.（2022·广东佛山·二模）已知sin，则___________.
【答案】
【详解】
所以
所以
故答案为：
4.（2022·广东肇庆·二模）若，则______．
【答案】
【详解】∵，
∴，
所以．
故答案为：.
5．（2022·广东深圳·二模）已知，则__________．
【答案】
【详解】解：由题意可知： .
6.若，且，则（ ）
A．B．C．2D．2
【答案】D
【详解】
，故，
可解得或，又，故，故，
故选：D
7．已知，则（ ）
A．B．C．D．
【答案】B
【详解】
因为，所以，
.
故选：B.
8．已知，且，则（ ）
A．B．C．D．
【答案】D
【详解】
因为，所以
又，所以，所以
所以
故选：D
9．已知，则（ ）
A．B．C．D．
【答案】B
【详解】
因为，
所以.
故选：B．
10．已知，，则（ ）
A．B．C．D．
【答案】B
【详解】
解：因为，所以，又，
所以，
所以。
即，所以
故选：B
【巩固练习】
一、单选题
1．已知角与角的顶点均与原点O重合，始边均与x轴的非负半轴重合，它们的终边关于x轴对称．若，则（ ）
A．B．C．D．
【答案】A
【详解】
因为与关于轴对称，，
所以，，
则，，，，
当时，，
，
当时，，
所以，
故选：A．
2．已知，，则（ ）
A．0B．C．D．1
【答案】C
【详解】
因为，，
两式平方相加得： ，
即 ，即，
则，
故即，，即，
即，，即，
故，
故选：C
3．已知，，则（ ）
A．B．C．1D．2或6
【答案】A
【详解】
因为，所以，解得，
又，所以.
故选:A.
4．公元前6世纪，古希腊的毕达哥拉斯学派研究过正五边形和正十边形的作图，发现了黄金分割约为0.618，这一数值也可以表示为，若，则（ ）
A．－4B．－2C．2D．4
【答案】B
【详解】
．
故选：B．
5．若，则的值为（ ）
A．B．C．D．
【答案】D
【详解】
由，可得
又，则
故选：D
6．若，则（ ）
A． B． C．D．
【答案】C
【详解】
，
因为
所以，，
因为，，
所以，，
则．
故选：C
二、多选题
7．已知，，则（ ）
A．B．C．D．
【答案】BD
【详解】
因为， 所以，又 ，
所以，，故A错误，B正确．，
所以，，
故C错误，D正确．
故选：BD.
8．下列各式的值为的是（ ）.
A．sin B．sincs C．D．
【答案】AD
【详解】
A：，符合题意；
B：，不符合题意；
C：，不符合题意；
D：，符合题意，
故选：AD
9．已知，其中为锐角，则以下命题正确的是（ ）
A．B．
C．D．
【答案】AB
【详解】
因为，，
所以，故A正确；
因为，
所以
所以
，故B正确；
，
，
由得，，解得；故C不正确；
由得，，解得；
，故D不正确.
故选：AB.
三、填空题
10．若，则__________，_________．
【答案】
【详解】
，∴，即，
即，令，，
则，∴，即，
∴ ，
则．
故答案为：；．
11．已知，则________.
【答案】
【详解】
因为，，
所以，
所以
，所以，
，所以，
则.
故答案为：.
12．已知 ，则_____________ .
【答案】
【详解】
因为
所以.
.
故答案为：
13．__________.
【答案】0
【详解】
.
故答案为：0．
四、解答题
14．已知，．
(1)求的值；
(2)若，，求的值．
【答案】(1) (2)
【解析】
(1)
解：因为，，
又，所以，
所以.
(2)
解：因为，
，
又因为，所以，
由（1）知，，
所以．
因为，，则，所以．
15．已知角为锐角，，且满足，
(1)证明：；
(2)求.
【答案】(1)证明见解析
(2)
【解析】
(1)
证明：因为，
所以，
因为为锐角且函数在上单调递增，所以
(2)
由，结合角为锐角，解得，，
因为，且 所以.
又，
所以
16．（1）已知，求的值；
（2）已知，，且，，求．
【答案】（1）；（2）
【详解】
（1）
；
（2）由可知，又，，
则，又，则，则，
又，则.