山东省临沂市沂南县2022-2023学年七年级上学期期末数学试题（含详细答案）

山东省临沂市沂南县2022-2023学年七年级上学期期末数学试题

学校:___________姓名：___________班级：___________考号：___________

一、单选题

1．下列各式中，是一元一次方程的是（     ）

A．x－y=2 B．3x+5=8 C．2x－3 D．

2．被誉为：“中国天眼”的世界上最大的单口径球面射电望远镜的反射面总面积约为，将250000用科学记数法可表示为（  ）

A． B． C． D．

3．如图，检测4个排球，其中质量超过标准的克数记为正数，不足的克数记为负数．最接近标准的是（    ）

A． B． C． D．

4．在，3.14，，0.1414，中，有理数的个数是（    ）

A．5个 B．4个 C．3个 D．2个

5．某同学用剪刀沿直线将一片平整的银杏叶剪掉一部分（如图），发现剩下的银杏叶的周长比原银杏叶的周长要小，能正确解释这一现象的数学知识是（　   　）

A．两点确定一条直线 B．点动成线 C．直线是向两方无限延伸的 D．两点之间线段最短

6．下列等式的变形中，正确的是（    ）

A．如果，那么 B．如果，那么

C．如果，那么 D．如果，那么

7．已知，，，下列结论正确的是（　　）

A．  B．

C．  D．以上均不正确

8．把方程去分母后，正确的是(    )．

A． B． C． D．

9．如图，甲从O地出发向北偏东方向走到A处，乙从O地出发向南偏东方向走到B处，则的度数是（    ）

A．90° B．100° C．105° D．110°

10．如图，数轴上A，B，C三点所表示的数分别为a，b，c，且．如果有，那么该数轴原点0的位置应该在（    ）

A．点A的左边 B．点A与B之间 C．点B与C之间 D．点C的右边

11．我国元朝朱世杰所著的《算学启蒙》中记载：“良马日行二百四十里，驽马日行一百五十里．驽马先行一十二日，问良马几何追及之．”意思是：“跑得快的马每天走240里，跑得慢的马每天走150里，慢马先走12天，快马几天可以追上慢马？”若设快马x天可以追上慢马，则可列方程为（    ）

A． B．

C． D．

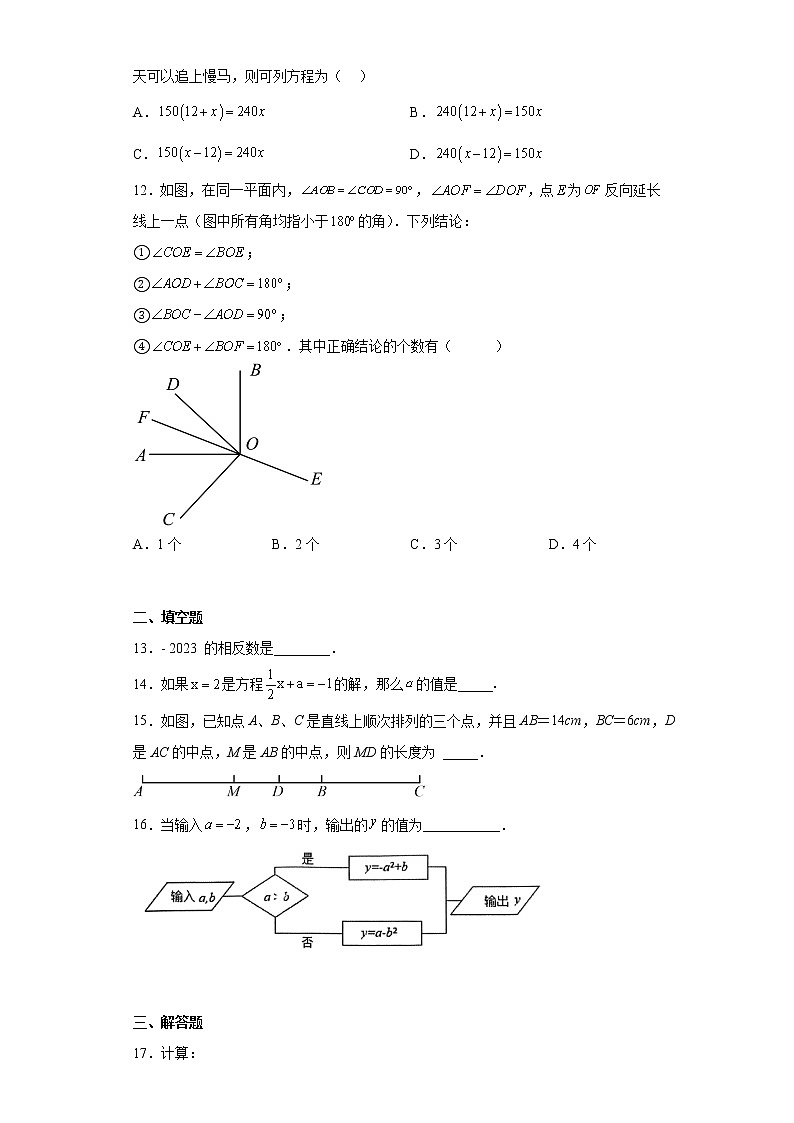
12．如图，在同一平面内，，，点为反向延长线上一点（图中所有角均指小于的角）．下列结论：

①；

②；

③；

④．其中正确结论的个数有（　　　）

A．1个 B．2个 C．3个 D．4个

二、填空题

13．- 2023 的相反数是________．

14．如果是方程的解，那么的值是_____．

15．如图，已知点A、B、C是直线上顺次排列的三个点，并且AB＝14cm，BC＝6cm，D是AC的中点，M是AB的中点，则MD的长度为 _____．

16．当输入，时，输出的的值为___________．

三、解答题

17．计算：

(1)

(2)．

18．解方程：．

19．小睿同学在做一道改编自课本上的习题时，解答过程如下：

(1)小睿同学的解答正确吗？如果正确，给出各步计算的依据；如果不正确，请给出正确的计算过程．

(2)当时，求此代数式的值．

20．体育课上全班男生进行了百米测试，达标成绩为秒，下面是第一小组8名男生的成绩记录，其中“”表示成绩大于秒，“”表示成绩小于秒．

(1)跑的最快的是百米跑了___________秒．

(2)这个小组男生百米测试的达标的有___________人．

(3)求这个小组8名男生的平均成绩是多少？

21．如图所示，已知线段a，b．

①作射线；

②在射线上依次截取；

③在线段上截取．

(1)由作图可知________．（用含a，b的式子表示）

(2)若，，E为线段的中点，F为线段的中点，求线段的长．

22．某车间为提高生产总量，在原有16名工人的基础上，新调入若干名工人，使得调整后车间的总人数是新调入工人人数的3倍多4人．

(1)求调入多少名工人；

(2)在（1）的条件下，每名工人每天可以生产240个螺栓或400个螺母，1个螺栓需要2个螺母，为使每天生产的螺栓和螺母刚好配套，应该安排生产螺栓和螺母的工人各多少名？

23．已知：点O是直线上的一点，，是的平分线．

(1)当点C、D、E在直线的同侧（如图1）时，

①若，求的度数．

②若，则_____________．（用含的式子表示）

(2)当点C与点D，E在直线的两侧（如图2）时，（1）中②的结论是有仍然成立？请给出你的结论并说明理由．

参考答案：

1．B

【分析】根据一元一次方程的定义逐个判断即可．

【详解】A、是二元一次方程，不是一元一次方程，故本选项不符合题意；

B、是一元一次方程，故本选项符合题意；

C、是代数式，不是方程，故本选项不符合题意；

D、未知数的最高次数不是1，此方程不是一元一次方程，故本选项不符合题意．

故选：B．

【点睛】本题考查了一元一次方程的定义，能熟记一元一次方程的定义的内容是解此题的关键，注意：只含有一个未知数，并且所含未知数的项的最高次数是1次的整式方程，叫一元一次方程．

2．B

【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．

【详解】250000=2.5×105，

故选：B．

【点睛】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．

3．D

【分析】求出超过标准的克数和低于标准的克数的绝对值，绝对值小的则是最接近标准的球．

【详解】解：通过求4个排球的绝对值得：

，，，，

的绝对值最小．

所以这个球是最接近标准的球．

故选：D．

【点睛】本题考查正数和负数，绝对值，解题的关键是明确正数和负数在题目中表示的实际意义．

4．B

【分析】根据有理数的定义，即可求解．

【详解】解：有理数有，3.14，，0.1414，有4个．

故选：B

【点睛】本题主要考查了有理数的定义，熟练掌握整数和分数统称为有理数是解题的关键．

5．D

【分析】根据两点之间，线段最短即可解答．

【详解】解：根据两点之间，线段最短，可知剩下的银杏叶的周长比原银杏叶的周长要小，

故能正确解释这一现象的数学知识是两点之间，线段最短

故选D．

【点睛】此题考查的是线段公理，掌握用两点之间，线段最短解释生活现象是解决此题的关键．

6．A

【分析】根据等式的性质和绝对值的意义逐项求解即可．

【详解】A．如果，那么两边都减去c可得，故正确；

B．当是，a、b相等或互为相反数，故不正确；

C．当时，满足，但x与 y不一定相等，故不正确；

D．如果，当时，不成立，故不正确；

故选：A．

【点睛】本题考查了等式的基本性质，正确掌握等式的性质是解题的关键．等式的基本性质1是等式的两边都加上（或减去）同一个整式，所得的结果仍是等式；等式的基本性质2是等式的两边都乘以（或除以）同一个数（除数不能为0），所得的结果仍是等式．

7．B

【分析】根据小单位化大单位除以进率，由，可得答案．

【详解】解：∵，

∴，

∵，，

∴，

故选：B．

【点睛】本题考查了度分秒的换算，小单位化大单位除以进率是解题关键．

8．D

【详解】试题解析：方程两边都乘以6得：3x-2（x-1）=6，

故选D．

点睛：解一元一次方程的步骤是去分母、去括号、移项、合并同类项、系数化成1．

9．B

【分析】首先求得与正东方向的夹角的度数，再求得与正东方向的夹角的度数，然后 等于这两个角的和，即可得到答案．

【详解】解：与正东方向的夹角的度数是：，

与正东方向的夹角的度数是：，

则，

故选：B

【点睛】本题考查了方位角，角的和差运算，解决此题时，能准确找到方位角是解题的关键．

10．C

【分析】根据各个选项的情况，去分析a，b，c三个数的正负，判断选项的正确性．

【详解】解：若原点在点A左边，则、、，就不满足，故A选项错误；

若原点在点A与点B之间，则、、，且，就不满足，故B选项错误；

若原点在点B与点C之间，则、、，条件都可以满足，故C选项正确；

若原点在点C右边，则、、，就不满足，故D选项错误．

故选：C．

【点睛】本题考查数轴，解题的关键是根据数轴上点的位置判断式子的正负．

11．A

【分析】直接根据相遇时所走路程相等列出一元一次方程即可得出答案．

【详解】设快马x天可以追上慢马，由题意可知：．

故选：A．

【点睛】本题考查了由实际问题抽象出一元一次方程，解题的关键是准确找出等量关系，正确列出一元一次方程．

12．C

【分析】由∠AOB=∠COD=90°，根据等角的余角相等得到∠AOC=∠BOD，结合即可判断①正确；由∠AOD+∠BOC=∠AOD+∠AOC+∠AOD+∠BOD，结合即可判断②正确；由∠BOC-∠AOD=∠AOC+90°-∠AOD，而不能判断∠AOD=∠AOC，即可判断③不正确；由E、O、F三点共线得∠BOE+∠BOF=180°，而∠COE=∠BOE，从而可判断④正确．

【详解】解：∵∠AOB=∠COD=90°，

∴∠AOC=∠BOD，

而∠AOF=∠DOF，

∴180°-∠AOC-∠AOF=180°-∠BOD-∠DOF，

即∠COE=∠BOE，所以①正确；

∠AOD+∠BOC=∠AOD+∠AOC+∠AOD+∠BOD=∠COD+∠AOB =180°，

所以②正确；

∠COB-∠AOD=∠AOC+90°-∠AOD，

而，所以③不正确；

∵E、O、F三点共线，

∴∠BOE+∠BOF=180°，

∵∠COE=∠BOE，

∴∠COE+∠BOF=180°，所以④正确．

所以，正确的结论有3个．

故选：C．

【点睛】题考查了余角和补角、角度的计算、余角的性质以及角平分线的定义等知识，准确识图是解题的关键．

13．2023

【分析】直接利用相反数的定义分析得出答案．

【详解】-2023的相反数是：2023．

故答案为：2023．

【点睛】本题主要考查了相反数，正确掌握相反数的定义是解题关键．

14．-2

【分析】此题可将x=2代入方程，然后得出关于a的一元一次方程，解方程即可得出a的值．

【详解】将x=2代入方程x+a=-1得1+a=-1，

解得：a=-2．

故答案为-2．

【点睛】此题考查的是一元一次方程的解法，方程两边可同时减去1，即可解出a的值．

15．3cm

【分析】由AB=14cm，BC=6cm，于是得到AC=20cm，根据线段中点的定义得到AD、AM的长，根据线段的和差得到MD=AD-AM，于是得到结论．

【详解】解：∵AB=14cm，BC=6cm．

∴AC=AB+BC=20cm，

∵D是AC的中点，

∴AD=AC=10cm；

∵M是AB的中点，

∴AM=AB=7cm，

∴DM=AD-AM=3cm．

故答案为：3cm．

【点睛】此题主要考查了两点之间的距离，线段的和差、线段的中点的定义，利用线段差及中点性质是解题的关键．

16．1

【分析】先根据有理数比较大小的方法求出，再把，代入中进行求解即可．

【详解】解：∵，，

∴，

∴，

故答案为：1．

【点睛】本题主要考查了与程序流程图有关的代数式求值，有理数比较大小，正确计算是解题的关键．

17．(1)23

(2)

【详解】（1）

；

（2）

．

【点睛】本题考查了有理数的混合运算，解题的关键是掌握运算法则和运算顺序．

18．

【分析】方程去分母，去括号，移项合并，把x系数化为1，即可求出解．

【详解】解：

去分母得，

去括号得，

移项得，

合并同类项得，

系数化为1得，．

【点睛】本题主要考查解一元一次方程，解题的关键是掌握解一元一次方程的基本步骤：去分母、去括号、移项、合并同类项、系数化为1．

19．(1)不正确，见解析

(2)

【分析】（1）观察小睿同学的解答过程，可知第一步去括号错误，根据去括号合并同类项的步骤写出正确的步骤；

（2）把代入（1）中化简的结果计算即可．

【详解】（1）解：不正确．

原式

；

（2）解：当时，

原式

．

【点睛】本题考查了整式的加减——化简求值，一般先把所给整式去括号合并同类项，再把所给字母的值或代数式的值代入计算．

20．(1)；

(2)5；

(3)秒．

【分析】（1）小于达标数越多，跑得越快；

（2）根据非正数是达标数，解得达标数，再将达标数除以总人数即可解题；

（3）计算数据的总和，再除以8即可解题．

【详解】（1）由题意可知：

，

故答案为：；

（2）由表格可知，达标的有5人．

（3），

，

答：这个小组8名男生的平均成绩是秒．

【点睛】本题考查了利用正负数解决实际问题的能力，关键是能准确理解正负数的意义，并结合实际问题列式计算．

21．(1)

(2)11

【分析】（1）由作图可知，，，根据可得答案；

（2）根据线段中点的定义得出，，由（1）可知，，根据可得答案．

【详解】（1）由作图可知，，，

．

故答案为：；

（2）为线段的中点，为线段的中点，，，

，，

由（1）可知，，

．

【点睛】本题考查作图基本作图，两点间的距离，线段中点的定义，解答此类题目时要注意线段之间的和差关系．

22．(1)调入6名工人

(2)10名工人生产螺栓，12名工人生产螺母，可使每天生产的螺栓和螺母刚好配套．

【分析】（1）设调入x名工人，根据“调整后车间的总人数是调入工人人数的3倍多4人”得：，可解得答案；

（2）设y名工人生产螺栓，由“1个螺栓需要2个螺母”，可得，即可解得答案．

【详解】（1）解：设调入x名工人，

根据题意得：，

解得，

∴调入6名工人；

（2）解：由（1）知，调入6名工人后，车间有工人（名），

设y名工人生产螺栓，则名工人生产螺母，

∵每天生产的螺栓和螺母刚好配套，

∴，

解得，

∴，

答：10名工人生产螺栓，12名工人生产螺母，可使每天生产的螺栓和螺母刚好配套．

【点睛】本题考查一元一次方程的应用，解题的关键是读懂题意，找到等量关系列方程．

23．(1)①，②．

(2)成立，理由见解析

【分析】（1）①根据，，求出，再根据角平分线得到，即可得到答案；②根据，，求出，再根据角平分线得到，即可得到答案；

（2）根据，，求出，再根据角平分线得到，即可得到答案．

【详解】（1）解：（①∵，，

∴，

∵平分，

∴；

∴

②∵，，

∴，

∵平分，

∴；

∴

故答案为；

（2）解：成立，理由如下，

∵，，

∴，

∵平分，

∴；

∴．

【点睛】本题考查角平分线分两个角相等都等于大角一半，及直角平角定义，解题的关键是根据直角等于，并用一个角表示出另一个角．