高中数学人教A版 (2019)选择性必修 第三册8.3 分类变量与列联表优秀课时作业

这是一份高中数学人教A版 (2019)选择性必修 第三册8.3 分类变量与列联表优秀课时作业，共5页。试卷主要包含了3 列联表与独立性检验，下列说法正确的是，2X+0等内容，欢迎下载使用。

1.下列关于独立性检验的说法中，错误的是（ ）
A.独立性检验依据小概率原理 B.独立性检验原理得到的结论一定正确
C.样本不同，独立性检验的结论可能有差异 D.独立性检验不是判定两类事物是否相关的唯一方法
2.在研究打鼾与患心脏病之间的关系中，通过收集数据、整理分析数据得到“打鼾与患心脏病有关”的结论，并且在犯错误的概率不超过0.01的前提下认为这个结论是成立的.下列说法中正确的是（ ）
A.100个心脏病患者中至少有99人打鼾 B.1个人患心脏病，则这个人有99%的概率打鼾
C.100个心脏病患者中一定有打鼾的人 D.100个心脏病患者中可能一个打鼾的人都没有
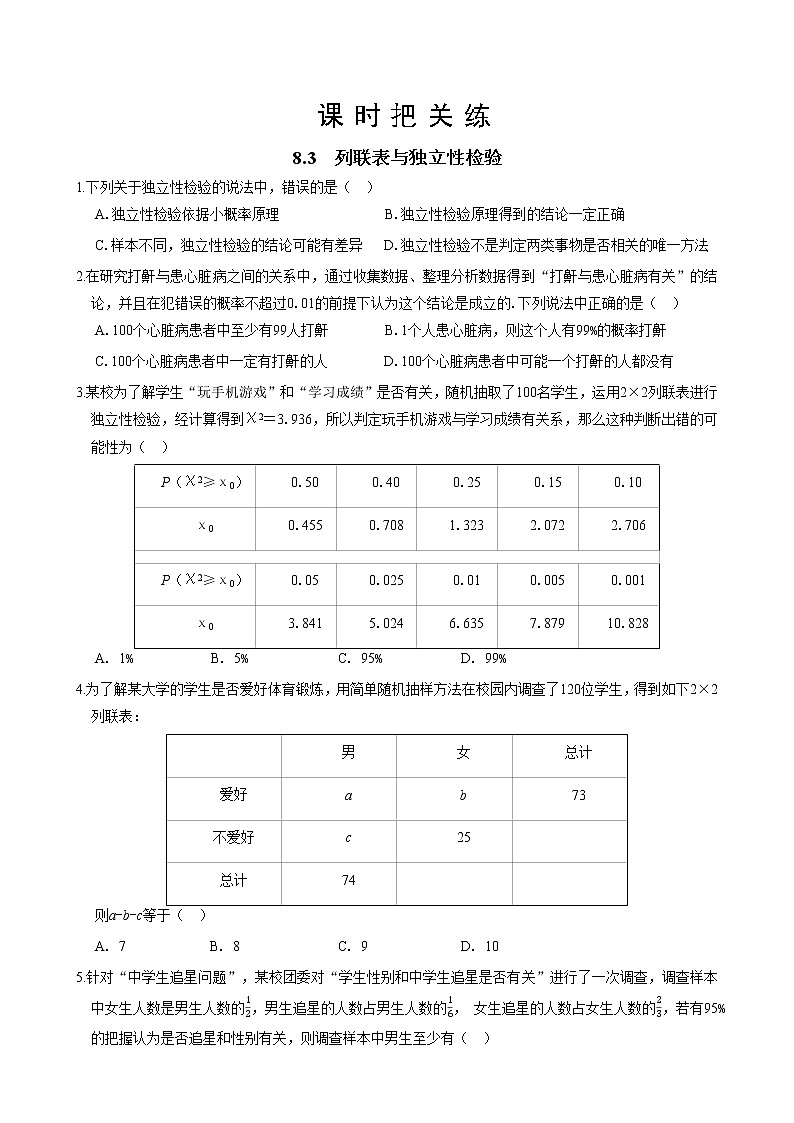
3.某校为了解学生“玩手机游戏”和“学习成绩”是否有关，随机抽取了100名学生，运用2×2列联表进行独立性检验，经计算得到χ2＝3.936，所以判定玩手机游戏与学习成绩有关系，那么这种判断出错的可能性为（ ）
A. 1%B. 5%C. 95% D. 99%
4.为了解某大学的学生是否爱好体育锻炼，用简单随机抽样方法在校园内调查了120位学生，得到如下2×2列联表：
则a-b-c等于（ ）
A. 7 B. 8 C. 9 D. 10
5.针对“中学生追星问题”，某校团委对“学生性别和中学生追星是否有关”进行了一次调查，调查样本中女生人数是男生人数的12，男生追星的人数占男生人数的16， 女生追星的人数占女生人数的23，若有95%的把握认为是否追星和性别有关，则调查样本中男生至少有（ ）
A. 12人 B. 11人 C. 10人 D. 18人
6.下列说法正确的是（ ）
A.两个变量的相关关系一定是线性相关
B.两个随机变量的线性相关性越强，则相关系数的绝对值就越接近于0
C.在线性回归方程Y＝0.2X+0.8中，当解释变量X每增加1个单位时，预报变量Y平均增加1个单位
D.对分类变量X与Y，随机变量χ2的观测值χ越大，则判断“X与Y有关系”的把握程度越大
7.两个分类变量X和Y，值域分别为{x1，x2}和{y1，y2}，其样本频数分别是a＝10，b＝21，c＋d＝35．若X与Y有关系的可信程度不小于95%，则c等于( )
A．3 B．7 C．5 D．6
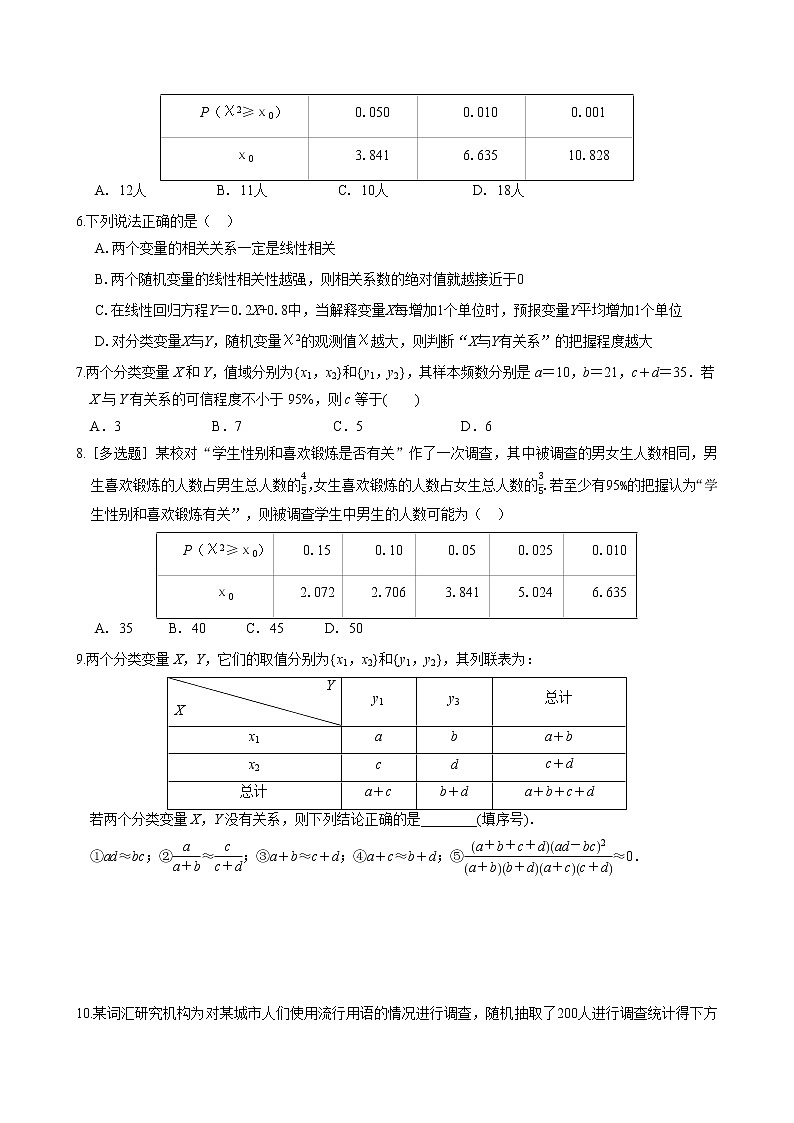
8.［多选题］某校对“学生性别和喜欢锻炼是否有关”作了一次调查，其中被调查的男女生人数相同，男生喜欢锻炼的人数占男生总人数的45，女生喜欢锻炼的人数占女生总人数的35.若至少有95%的把握认为“学生性别和喜欢锻炼有关”，则被调查学生中男生的人数可能为（ ）
A. 35B. 40C. 45D. 50
9.两个分类变量X，Y，它们的取值分别为{x1，x2}和{y1，y2}，其列联表为：
若两个分类变量X，Y没有关系，则下列结论正确的是________(填序号)．
①ad≈bc；②eq \f(a,a＋b)≈eq \f(c,c＋d)；③a＋b≈c＋d；④a＋c≈b＋d；⑤eq \f(a＋b＋c＋dad－bc2,a＋bb＋da＋cc＋d)≈0．
10.某词汇研究机构为对某城市人们使用流行用语的情况进行调查，随机抽取了200人进行调查统计得下方的2×2列联表.则根据列联表可知：
有 的把握认为“经常用流行用语”与“年轻人”有关系.
11.足不出户，手机下单，送菜到家，轻松逛起手机“菜市场”，拎起手机“菜篮子”，省心又省力.某手机App（应用程序）公司为了了解这款App使用者的人数及满意度，对一大型小区居民开展5个月的调查活动，得到对这款App不满意度的人数统计数据如下：
（1）请利用所给数据求不满意人数Y与月份X之间的回归直线方程Y＝bX+ a，并预测该小区10月份对这款App不满意的人数；
（2）工作人员发现使用这款App居民的年龄X近似服从正态分布N（35，42），求P（27< x≤47）的值；
（3）工作人员从这5个月内的调查表中随机抽查100人，调查是否使用这款App与性别的关系，得到下表：
你能否据此判断有99%的把握认为是否使用这款App与性别有关？
参考公式：b＝ i=1nxiyi−nxyi=1nxi2−nx2＝ i=1nxi−xyi−yi=1nxi−x2，a＝y- bx.
附：随机变量：ξ~N（μ，σ2），则P（μ−σ<ξ≤μ+σ）≈0.682 6，P（μ−2σ<ξ≤μ+2σ）≈0.9544，P（μ−3σ<ξ≤μ+3σ）≈0.997 4，χ2＝nad−bc2a+bc+da+cb+d（其中n＝a+b+c+d）.
P（χ2≥χ0）
0.50
0.40
0.25
0.15
0.10
χ0
0.455
0.708
1.323
2.072
2.706
P（χ2≥χ0）
0.05
0.025
0.01
0.005
0.001
χ0
3.841
5.024
6.635
7.879
10.828
男
女
总计
爱好
a
b
73
不爱好
c
25
总计
74
P（χ2≥χ0）
0.050
0.010
0.001
χ0
3.841
6.635
10.828
P（χ2≥χ0）
0.15
0.10
0.05
0.025
0.010
χ0
2.072
2.706
3.841
5.024
6.635
Y
X
y1
y3
总计
x1
a
b
a＋b
x2
c
d
c＋d
总计
a＋c
b＋d
a＋b＋c＋d
年轻人
非年轻人
总计
经常用流行用语
125
25
150
不常用流行用语
35
15
50
总计
160
40
200
月份
1
2
3
4
5
不满意的人数
120
105
100
95
80
使用App
不使用App
合计
女性
48
12
60
男性
22
18
40
合计
70
30
100
P（χ2≥χ0）
0.15
0.10
0.05
0.025
0.010
χ0
2.072
2.706
3.841
5.024
6.635
课时把关练
8.3 列联表与独立性检验
参考答案
1.B 2.D 3.B 4.C 5.A 6.D 7.A 8.CD
9.①②⑤ 10. 95%
11.解：（1）由表中的数据可知，x＝1+2+3+4+55＝3，y＝120+105+100+95+805＝100，
所以b＝i=15xiyi−5x yi=15xi2−5x2＝1 410−1 50055−45＝-9，故a＝y-bx＝100-（-9）×3＝127，
所以所求的回归直线方程为Y＝-9X+127.
令X＝10，则Y＝-9×10+127＝37（人），
所以预测10月份该小区对这款App不满意的人数为37.
（2）依题意得P（27≈0.954 4+0.997 4−0.954 42≈0.954 4+0.997 42＝0.975 9.
（3）由表中的数据计算可得：
χ2＝100×48×18−22×12260×40×70×30＝507≈7.143>6.635，
根据临界值可得，有99%的把握认为是否使用这款App与性别有关.