第一章 1.2空间向量在立体几何中的应用 1.2.2空间中的平面与空间向量（同步练习含答案）

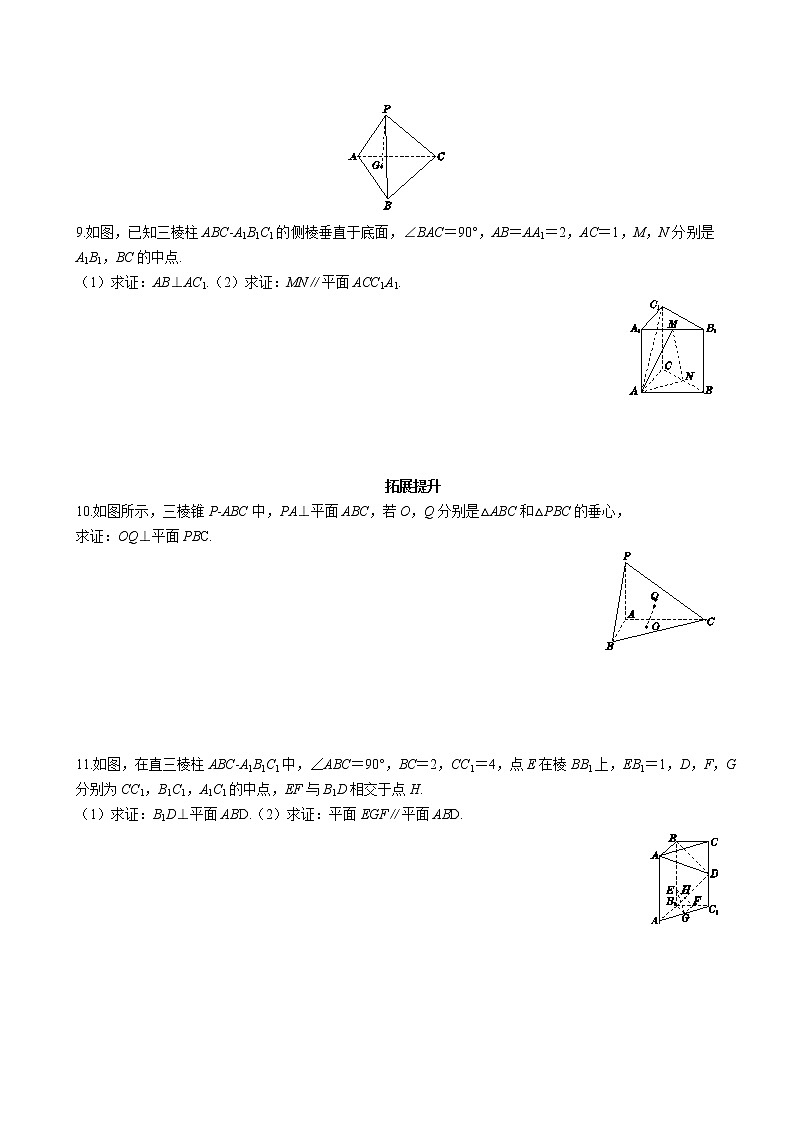
  课时把关练1.2  空间向量在立体几何中的应用 1.2.2　空间中的平面与空间向量基础巩固1.［多选题］下列命题中正确的是（　）A. 已知直线l垂直于平面α，向量a与直线l平行，则a是平面α的一个法向量B. 一个平面的法向量有无数个，任意两个都是共线向量C. 若平面外的一条直线的方向向量与平面的法向量垂直，则该直线与平面平行D. 直线的方向向量与平面的法向量的方向相同或相反时，直线与平面垂直2.若a＝是平面α的一个法向量，且b＝（-1，2，1），c＝与平面α都平行，则向量a等于（　）A.   B.       C.     D.3.若向量＝（1，2，3），＝（3，2，1），则平面ABC的一个法向量为（　）A.（-1，2，-1）       B.（1，2，1）          C.（1，2，-1）         D.（-1，2，1）4.如图，在正方体ABCD-A1B1C1D1中，以D为原点建立空间直角坐标系Oxyz，E，F分别在棱BB1，CC1上，且B1E＝2EB，CF＝2FC1，则下列向量中，能作为平面AEF的法向量的是（　）A.（1，-1，3）       B.（1，-1，-3）     C.（2，-3，6）          D.（-2，3，-6） 5.已知平面α的一个法向量是（2，3，-1），平面β的一个法向量是（4，λ，-2），若α∥β，则λ的值是（　）A.               B. 6                C. -6                 D. 6.若平面α，β的法向量分别为n1＝（2，-3，5），n2＝（-3，1，-4），则（　）A. α∥β          B. α⊥β        C. α，β相交但不垂直      D. 以上均不正确7.已知m＝，n＝（-4，1，1）分别是平面α，β的法向量，若α⊥β，则k＝（　）A. -2           B. -1           C.            D. 28.如图所示，在三棱锥P-ABC中，PA⊥BC，PB⊥AC，点G是P在平面ABC内的射影，则G是△ABC的（　）A. 内心            B. 外心         C. 垂心        D. 重心9.如图，已知三棱柱ABC-A1B1C1的侧棱垂直于底面，∠BAC＝90°，AB＝AA1＝2，AC＝1，M，N分别是A1B1，BC的中点.（1）求证：AB⊥AC1.（2）求证：MN∥平面ACC1A1.    拓展提升10.如图所示，三棱锥P-ABC中，PA⊥平面ABC，若O，Q分别是△ABC和△PBC的垂心，求证：OQ⊥平面PBC.     11.如图，在直三棱柱ABC-A1B1C1中，∠ABC＝90°，BC＝2，CC1＝4，点E在棱BB1上，EB1＝1，D，F，G分别为CC1，B1C1，A1C1的中点，EF与B1D相交于点H.（1）求证：B1D⊥平面ABD.（2）求证：平面EGF∥平面ABD. 　   课时把关练1.2  空间向量在立体几何中的应用 1.2.2　空间中的平面与空间向量参考答案1. BCD   2. D   3. A   4.A   5. B   6. C   7.B   8. C   9. 证明：∵ 三棱柱为直三棱柱，∴ AA1⊥平面ABC，∴ AA1⊥AC，AA1⊥AB.又∠BAC＝90°，则AB，AC，AA1两两互相垂直，可建立如图所示的空间直角坐标系，则A（0，0，0），B（0，2，0），C1（-1，0，2），M（0，1，2），N.（1）∵＝（0，2，0），＝（-1，0，2），∴·＝0×（-1）+2×0+0×2＝0，∴ AB⊥AC1.（2）由题意知，是平面ACC1A1的一个法向量.∵＝（0，2，0），＝，∴·＝0×+2×0+0×（-2）＝0，∴⊥.∵ MN平面ACC1A1，∴ MN∥平面ACC1A1.10.证明：如图，连接AO并延长交BC于点E，连接PE.∵ PA⊥平面ABC，AE⊥BC（由于O是△ABC的垂心），∴ PE⊥BC（三垂线定理），∴ 点Q在PE上.∴BC⊥平面PAEBC⊥OQ.①连接BO并延长交AC于点F，则BF⊥AC.连接BQ并延长交PC于点M，则BM⊥PC.连接MF.∵ PA⊥平面ABC，BF⊥AC，∴ BF⊥PC（三垂线定理）.∴PC⊥平面BMFPC⊥OQ.②由①②，知OQ⊥平面PBC.11. 证明：（1）如图所示，建立空间直角坐标系，设AB＝a，则B1（0，0，0），F（0，1，0），E（0，0，1），A（a，0，4），B（0，0，4），D（0，2，2），，所以＝（0，2，2），＝（-a，0，0），＝（0，2，-2），所以·＝0+0+0＝0，·＝0+4-4＝0，所以⊥，⊥，所以B1D⊥AB，B1D⊥BD.又AB∩BD＝B，所以B1D⊥平面ABD.（2）由（1）可得＝（-a，0，0），＝（0，2，-2），＝，＝（0，1，-1），所以＝，＝，所以∥，∥，所以GF∥AB，EF∥BD.又GF∩EF＝F，AB∩BD＝B，所以平面EGF∥平面ABD.