
2022-2023学年福建省泉州市九年级上册数学期中专项突破模拟试卷(含解析)
展开一、选择题
1. 己知关于x的二次函数的图象经过原点,则m为( )
A. 1B. C. 1或D. 0
2. 如图,在网格中,A、B均为格点,以点A为圆心,以的长为半径作弧,图中的点C是该弧与网格线的交点,则的值是( )
A. B. C. D.
3. 如图,线段CD两个端点的坐标分别为C(﹣1,﹣2),D(﹣2,﹣1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的2倍,得到线段AB,则线段AB的中点E的坐标为( )
A (3,3)B. ()
C. (2,4)D. (4,2)
4. 三角函数之间的大小关系是( )
A. B.
C. D.
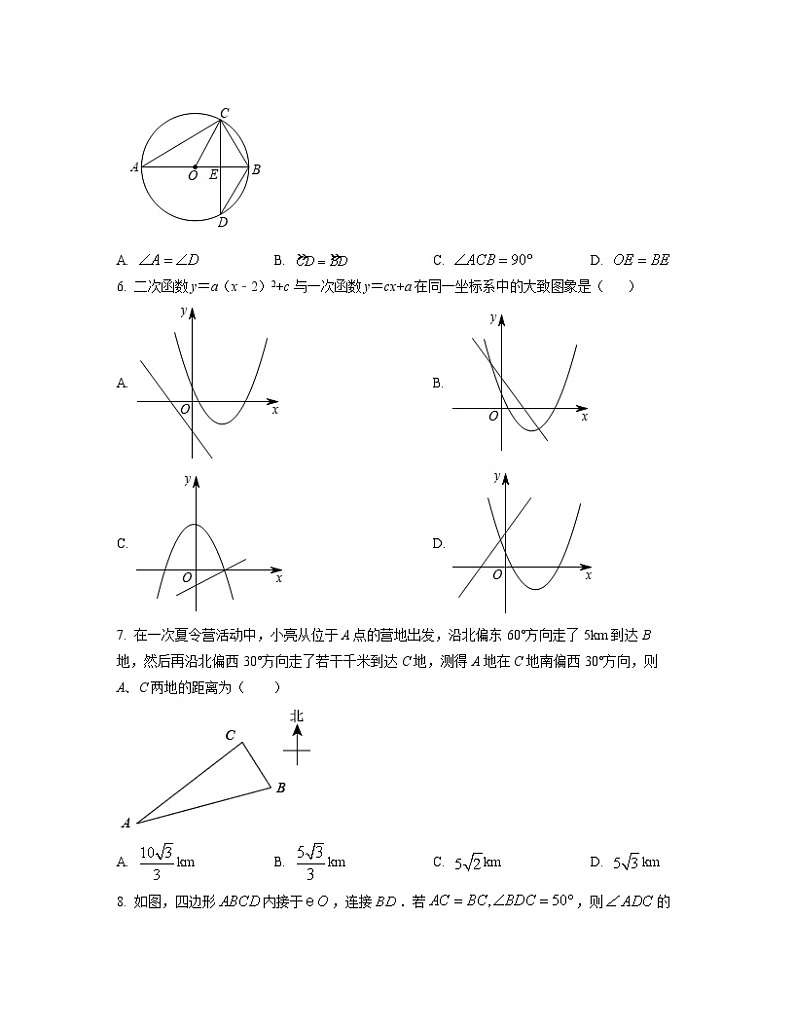
5. 如图,是的直径,为弦,且交于点E,则下列结论中不一定成立的是( )
A. B. C. D.
6. 二次函数y=a(x﹣2)2+c与一次函数y=cx+a在同一坐标系中的大致图象是( )
A. B.
C. D.
7. 在一次夏令营活动中,小亮从位于A点的营地出发,沿北偏东60°方向走了5km到达B地,然后再沿北偏西30°方向走了若干千米到达C地,测得A地在C地南偏西30°方向,则A、C两地的距离为( )
A. kmB. kmC. kmD. km
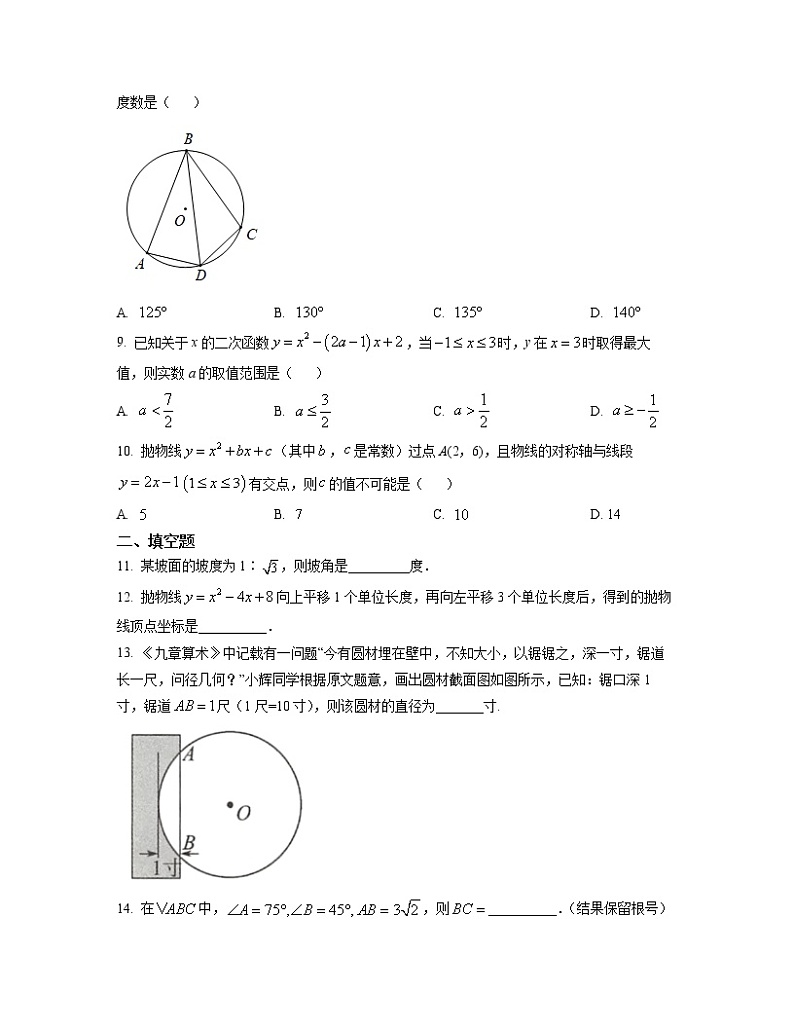
8. 如图,四边形内接于,连接.若,则的度数是( )
A. B. C. D.
9. 已知关于x的二次函数,当时,y在时取得最大值,则实数a的取值范围是( )
A. B. C. D.
10. 抛物线(其中,是常数)过点A(2,6),且物线的对称轴与线段有交点,则的值不可能是( )
A. B. C. D. 14
二、填空题
11. 某坡面的坡度为1∶,则坡角是_________度.
12. 抛物线向上平移1个单位长度,再向左平移3个单位长度后,得到的抛物线顶点坐标是__________.
13. 《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深1寸,锯道尺(1尺=10寸),则该圆材的直径为_______寸.
14. 在中,,则__________.(结果保留根号)
15. 如图,人工喷泉有一个竖直的喷水枪,喷水口A距地面,喷出水流的运动路线是抛物线,如果水流的最高点P到喷水枪所在直线的距离为,且到地面的距离为,则水流的落地点C到水枪底部B的距离为__________m.
16. 二次函数的图象过、、、四个点,①若,则一定有;②若,则可能;③若,则一定有;④若,则可能;以上说法中正确有__________.(填序号)
三、解答题
17 计算:
18. 如图,△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2)(正方形网格中,每个小正方形的边长均是1个单位长度).
(1)△A1B1C1与△ABC关于x轴成轴对称,请画出△A1B1C1,并写出C1点的坐标;
(2)以点B1为位似中心,将△A1B1C1放大得到△A2B1C2,放大前后面积之比为1:4,画出△A2B1C2,使它与△A1B1C1在位似中心同侧,并写出C2点的坐标;
(3)连接AC2、CC2,判断△ACC2的形状并直接写出结论.
19. 如图,己知抛物线与x轴交于A,B两点,与y轴交于点C.
(1)求A,B,C三点围成的三角形面积;
(2)点P是第一象限抛物线上的一个动点,并且∠POB的正切值为,求点P的坐标.
20. 如图,在四边形中,,过三点的圆交边于点E.
(1)求证:E是的中点;
(2)若,求证:.
21. 如图,某大楼的顶部竖有一块广告牌,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为,沿坡面向上走到B处测得广告牌顶部C的仰角为,己知山坡的坡度,米,米.
(1)求点B距水平地面的高度;
(2)若市政规定广告牌的高度不得大于7米,请问该公司的广告牌是否符合要求,并说明理由.(测角器的高度忽略不计,结果精确到0.1米,参考数据:,,,,)
22. 材料:如图1,和是的两条弦(即折线是圆的一条折弦),,M是的中点,则从M向所作垂线的垂足D是折弦的中点,即.下面是运用“截长法”证明的部分证明过程.
证明:如图2,在上截取,连接和,∵M是的中点,∴,……
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)如图3,已知内接于,D是的中点,依据(1)中的结论可得图中某三条线段的等量关系为__________;
(3)如图4,已知等腰内接于,D为上一点,连接于点E,的周长为,请求出的长.
23. 2020年体育中考,增设了考生进入考点需进行体温检测的要求.防疫部门为了解学生错峰进入考点进行体温检测的情况,调查了一所学校某天上午考生进入考点的累计人数(人)与时间(分钟)的变化情况,数据如下表:(表中9-15表示)
(1)根据这15分钟内考生进入考点的累计人数与时间的变化规律,利用初中所学函数知识求出与之间的函数关系式;
(2)如果考生一进考点就开始测量体温,体温检测点有2个,每个检测点每分钟检测20人,考生排队测量体温,求排队人数最多时有多少人?全部考生都完成体温检测需要多少时间?
(3)在(2)的条件下,如果要在12分钟内让全部考生完成体温检测,从一开始就应该至少增加几个检测点?
24. 如图①,在和中,,,.现将绕着点旋转一定角度后,再平移线段得到线段(点与点对应),连接,.
(1)如图②,当点在线段的延长线上时,求线段的长;
(2)当点与点在直线的同侧时,探究与的数量关系和位置关系,并说明理由;
(3)连接,求线段长的最大值.
25 已知抛物线与直线.
(1)如图1,若抛物线C与直线l只有一个交点A.
①求点A的坐标;(用含a的代数式表示)
②连接点A与点交抛物线C于另一点B,求的值.
(2)如图2,若抛物线C与直线l交于D,B两点(点D在点E左侧),连接,当时,判断a与b的积是否为定值若是,求出该定值;若不是,说明理由.
答案解析
一、选择题
【1题答案】
【正确答案】A
【2题答案】
【正确答案】B
【3题答案】
【正确答案】A
【4题答案】
【正确答案】A
【5题答案】
【正确答案】D
【6题答案】
【正确答案】B
【7题答案】
【正确答案】A
【8题答案】
【正确答案】B
【9题答案】
【正确答案】B
【10题答案】
【正确答案】A
二、填空题
【11题答案】
【正确答案】30
【12题答案】
【正确答案】
【13题答案】
【正确答案】26
【14题答案】
【正确答案】##
【15题答案】
【正确答案】##
【16题答案】
【正确答案】②③④
三、解答题
【17题答案】
【正确答案】-1
【18题答案】
【正确答案】(1)图见解析,C1(2,﹣2);(2)图见解析,C2(1,0);(3)△ACC2是等腰直角三角形
【19题答案】
【正确答案】(1)6 (2)点P的坐标为(,).
【20题答案】
【正确答案】(1)见解析;(2)见解析
【21题答案】
【正确答案】(1)5米 (2)该公司的广告牌符合要求,理由见解析
【22题答案】
【正确答案】(1)该证明的剩余部分见解析
(2)
(3)4
【23题答案】
【正确答案】(1);(2)队人数最多时是490人,全部考生都完成体温检测需要20.25分钟;(3)至少增加2个检测点
【24题答案】
【正确答案】(1)6;(2),,理由见解析;(3)
【25题答案】
【正确答案】(1)①,②
(2)a与b的积是定值,定值是14,理由见解析时间(分钟)
0
1
2
3
4
5
6
7
8
9
9~15
人数(人)
0
170
320
450
560
650
720
770
800
810
810
2022-2023学年福建省泉州市中考数学专项突破仿真模拟卷(一模二模)含答案: 这是一份2022-2023学年福建省泉州市中考数学专项突破仿真模拟卷(一模二模)含答案,共54页。
2022—2023学年福建省泉州市八年级下册数学期末专项突破模拟试卷(含解析): 这是一份2022—2023学年福建省泉州市八年级下册数学期末专项突破模拟试卷(含解析),共12页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年福建省泉州市九年级上册数学期中专项提升模拟试卷(含解析): 这是一份2022-2023学年福建省泉州市九年级上册数学期中专项提升模拟试卷(含解析),共9页。试卷主要包含了选择题.,填空题.,解答题.等内容,欢迎下载使用。












