2022-2023学年乌鲁木齐市九年级上册数学期末专项突破仿真模拟试卷（含解析）

这是一份2022-2023学年乌鲁木齐市九年级上册数学期末专项突破仿真模拟试卷（含解析），共9页。试卷主要包含了请将答案正确填写在答题卡上，方程的根的情况是等内容，欢迎下载使用。

注意事项：
1．答题前填写好自己的姓名、班级、考号等信息
2．请将答案正确填写在答题卡上
一、单选题（每小题5分，共45分）
1．下面图形中是轴对称图形不是中心对称图形的是（ ）
A．B．
C．D．
2．打开新华字典，恰好找到汉字“数”，这个事件是（ ）
A．必然事件B．随机事件C．不可能事件D．确定事件
3．方程的根的情况是（ ）
A．没有实数根B．有两个相等的实数根
C．有两个不相等的实数根D．有一个实数根
4．如图，点A，B，C，D，E在⊙O上，AB＝CD，∠E＝15°，则∠A＝（ ）
A．70°B．75°C．80°D．60°
5．如图将△ABC绕点C逆时针旋转得到△A’B’C，点B恰好落在A’B’上，若，则旋转角为（ ）
A．30°B．35°C．40°D．45°
6．已知抛物线为常数，与轴交于，两点（点在点的左侧），下列关于该抛物线的描述中，说法正确的是（ ）
A．该抛物线的有最高点
B．
C．点在轴的正半轴
D．当时，函数随的增大而增大
7．新冠疫情牵动人心，若有一人感染了新冠，在每轮传染中平均一个人可以传染个人，经过两轮传染后共有169人感染，若不加以控制，第三轮传染后感染人数为（ ）
A．338B．256C．2197D．2028
8．如图，P是等边三角形ABC内一点，将△ACP绕点A顺时针旋转60°得到△ABQ，若PA＝，PB＝ ，，则四边形APBQ的面积为（ ）
A．B． C．D．
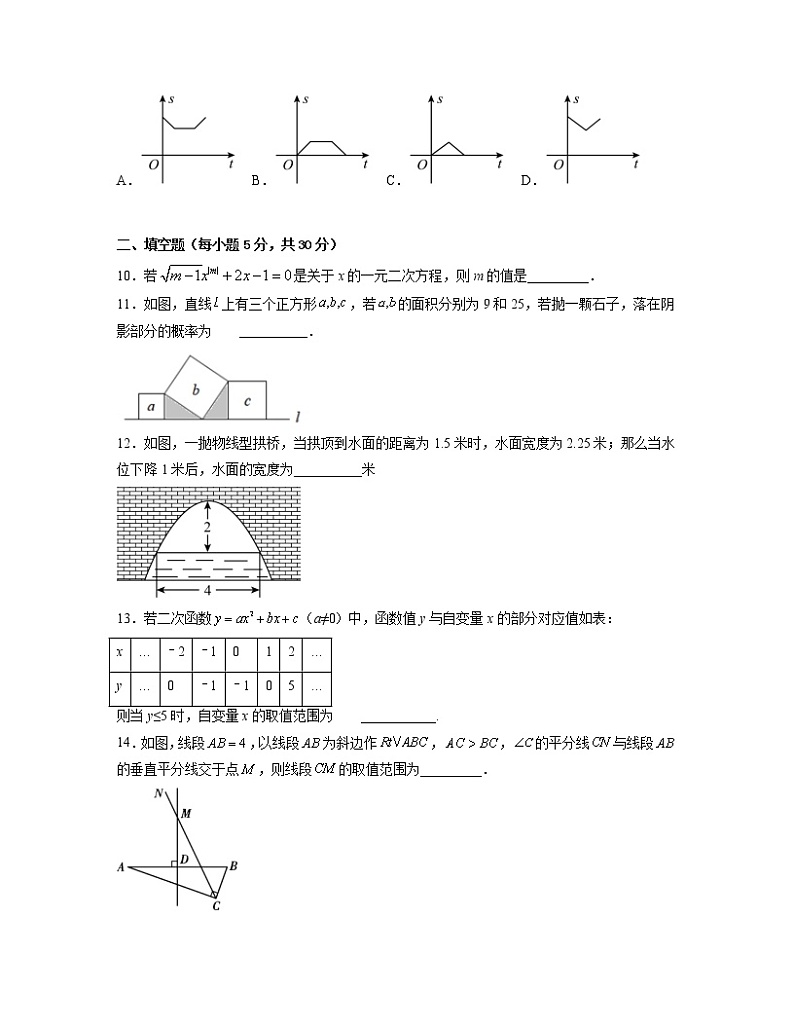
9．如图所示，半径为的圆和边长为的正方形在同一水平线上，圆沿该水平线从左向右匀速穿过正方形，设穿过的时间为，圆与正方形重叠部分阴影部分的面积为S，则S与的函数关系式的大致图象为（ ）
A．B．C．D．
二、填空题（每小题5分，共30分）
10．若是关于x的一元二次方程，则m的值是_________．
11．如图，直线上有三个正方形，若的面积分别为9和25，若抛一颗石子，落在阴影部分的概率为 __________．
12．如图，一抛物线型拱桥，当拱顶到水面的距离为1.5米时，水面宽度为2.25米；那么当水位下降1米后，水面的宽度为__________米
13．若二次函数（a≠0）中，函数值y与自变量x的部分对应值如表：
则当y≤5时，自变量x的取值范围为 ___________.
14．如图，线段，以线段为斜边作，，的平分线与线段的垂直平分线交于点，则线段的取值范围为_________．
15．如图，长方形中，，为上一点，且为边上的一个动点，连接，将绕着点顺时针旋转到的位置，连接和，则的最小值为___________．
三、解答题（共75分）
16．（8分）解下列一元二次方程：
(1)
(2)
17．（8分）已知关于的一元二次方程．
(1)不解方程，判断此方程根的情况；
(2)若是该方程的一个根，求代数式的值．
18．（9分）国家规定，中小学生每天在校体育活动时间不低于1h，为了解这项政策的落实情况，有关部门就“你每天在校体育活动时间是多少”的问题，在某校随机抽查了部分学生，再根据活动时间t（h）进行分组（A组：，B组：，C组：，D组：），绘制成如图所示的两幅不完整统计图，请根据图中信息回答问题：
(1)此次抽查的学生为_______人；
(2)补全条形统计图；
(3)从抽查的学生中随机询问一名学生，该生当天在校体育活动时间低于1小时的概率是多少？
(4)若当天在校学生为1200人，请估计在当天达到国家规定体育活动时间的学生有多少人？
19．（8分）如图，学校准备利用学校仓库旁一块空地，开辟一个矩形花圃，打算一面利用长为15米的墙面，三面利用长为31米的旧围栏，且矩形花圃正面留有一米宽的门．
(1)若矩形的面积为120米求矩形花圃的宽AB．
(2)当矩形花圃的宽AB为多少米时，所开辟的矩形花圃面积最大？（AB为正整数）
20．（8分）如图，在正方形ABCD中，射线AE与边CD交于点E，将射线AE绕点A顺时针旋转，与CB的延长线交于点F，，连接FE．
(1)求证：；
(2)若，，求的面积．
21．（10分）某地新茶上市，一茶商在该地收购新茶，茶商经过包装处理试销数日发现，平均每斤茶叶利润为20元，并且每天可售出60斤．进一步根据茶叶市场调查发现，销售单价每增加5元，每天销售量会减少10斤．设销售单价每增加元，每天售出斤．
(1)求与的函数关系式；
(2)求该茶商每天的最大利润．
22．（11分）如图，是半圆的直径，是半圆上不同于，的一点，作，过点作于点，的延长线与的延长线相交于点．
(1)求证：是半圆所在圆的切线；
(2)若，，求BE．
23．（13分）已知抛物线（a为常数，）交x轴于点A（6，0），点，交y轴于点C．
(1)求点C的坐标和抛物线的解析式；
(2)P是抛物线上位于直线AC上方的动点，过点P作y轴平行线，交直线AC于点D，当PD取得最大值时，求点P的坐标；
(3)M是抛物线的对称轴l上一点，N为抛物线上一点；当直线AC垂直平分的边MN时，求点N的坐标．
答案：
1．C
2．B
3．C
4．B
5．C
6．B
7．C
8．B
9．B
10．2
11．
12．
13．3≤x≤2
14．
15．
16．(1)，；
(2)，．
17．(1)
(2)6
18．(1)200
(2)
(3)
(4)816人
19．(1)AB长度为10米
(2)当矩形花圃的宽AB为9米时，所开辟的矩形花圃面积最大
20．(1)
(2)8
21．(1)
(2)1250元
22．(1)
(2)2
23．(1)C（0，6）；抛物线的解析式为y＝−x2＋5x＋6
(2)P（3，12）
(3)点N的坐标为或x
…
2
1
0
1
2
…
y
…
0
1
1
0
5
…