2022-2023学年江苏省盐城市亭湖区九年级（上）期末数学试卷（含解析）

这是一份2022-2023学年江苏省盐城市亭湖区九年级（上）期末数学试卷（含解析），共23页。试卷主要包含了选择题，填空题，计算题，解答题等内容，欢迎下载使用。
1. 下列图形中，既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2. 函数y=(x+1)2−3的最小值是( )
A. 1B. −1C. 3D. −3
3. 从拼音“shuxue”中随机抽取一个字母，抽中字母u的概率为( )
A. 13B. 14C. 15D. 16
4. 关于x的一元二次方程mx2−4x−1=0有两个不相等的实数根，则m的取值范围是( )
A. m≥−4B. m≥−4且m≠0C. m>−4D. m>−4且m≠0
5. 随着网络的发展，在节日期间长辈们往往用抢微信红包的形式发放红包，下表是针对某班同学们在春节期间所抢的红包金额进行统计的结果表：
根据表中提供的信息，红包金额的众数和中位数分别是( )
A. 16元，50元B. 30元，30元C. 30元，40元D. 30元，50元
6. 乐乐是一名职业足球队员，根据以往比赛数据统计，乐乐进球的概率为15，他明天将参加一场比赛，下面几种说法正确的是( )
A. 乐乐明天肯定进球B. 乐乐明天有可能进球
C. 乐乐明天比赛每射球5次必进球1次D. 乐乐明天的进球率为10%
7. 若抛物线y=−x2+bx+c经过点(−2,3)，则c−2b的值是( )
A. 7B. −1C. −2D. 3
二、填空题（本大题共10小题，共30.0分）
8. 一元二次方程x2=−x的根是______．
9. 抛物线y=−2(x+2)2+5的顶点坐标是______．
10. 甲、乙两人在相同条件下进行射击练习，每人10次射击成绩的平均数都是8环，方差分别为S甲2=1.4，S乙2=0.6，则两人射击成绩比较稳定的是______ (填“甲”或“乙”)．
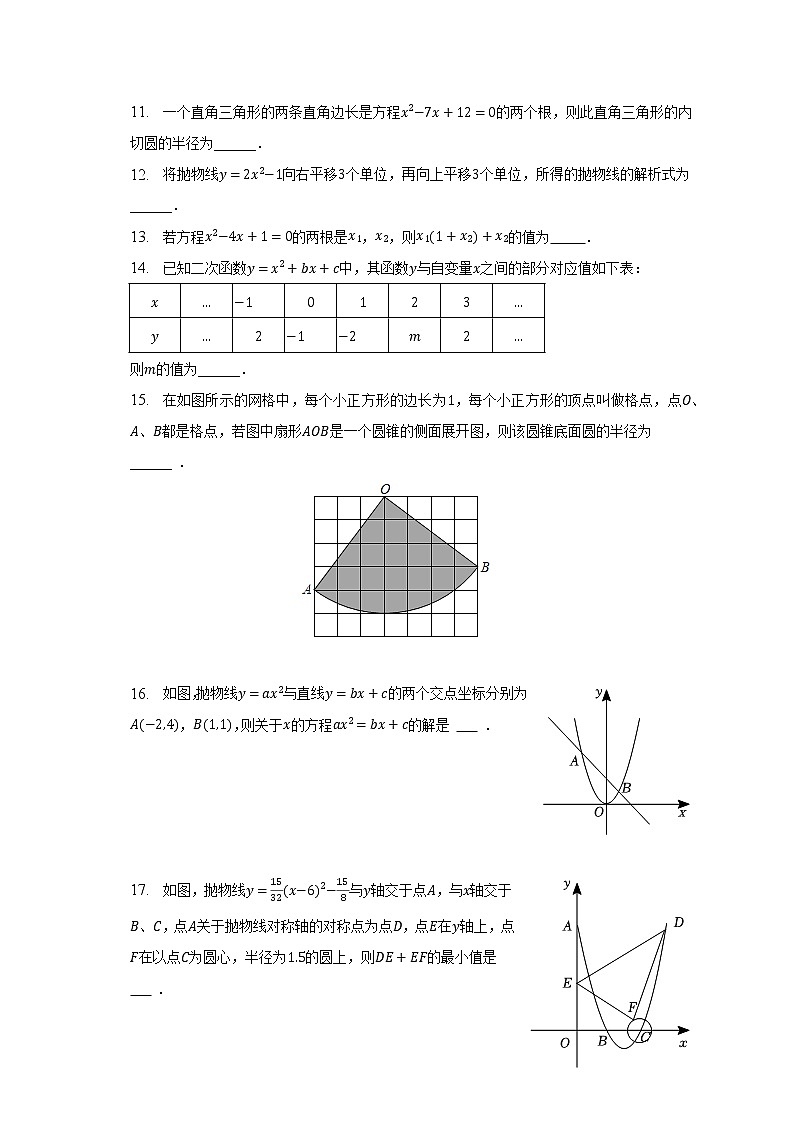
11. 一个直角三角形的两条直角边长是方程x2−7x+12=0的两个根，则此直角三角形的内切圆的半径为______．
12. 将抛物线y=2x2−1向右平移3个单位，再向上平移3个单位，所得的抛物线的解析式为______．
13. 若方程x2−4x+1=0的两根是x1，x2，则x1(1+x2)+x2的值为 ．
14. 已知二次函数y=x2+bx+c中，其函数y与自变量x之间的部分对应值如下表：
则m的值为______．
15. 在如图所示的网格中，每个小正方形的边长为1，每个小正方形的顶点叫做格点，点O、A、B都是格点，若图中扇形AOB是一个圆锥的侧面展开图，则该圆锥底面圆的半径为______ ．
16. 如图，抛物线y=ax2与直线y=bx+c的两个交点坐标分别为A(−2,4)，B(1,1)，则关于x的方程ax2=bx+c的解是 ．
17. 如图，抛物线y=1532(x−6)2−158与y轴交于点A，与x轴交于B、C，点A关于抛物线对称轴的对称点为点D，点E在y轴上，点F在以点C为圆心，半径为1.5的圆上，则DE+EF的最小值是 ．
三、计算题（本大题共1小题，共6.0分）
18. 如图，足球场上守门员在O处开出一记手跑高球，球从地面1.4米的A处抛出(A在y轴上)，运动员甲在距O点6米的B处发现球在自己头的正上方达到最高点M，距地面3.2米高，球落地点为C点．
(1)求足球开始抛出到第一次落地时，该抛物线的解析式．
(2)足球第一次落地点C距守门员多少米？
四、解答题（本大题共8小题，共64.0分。解答应写出文字说明，证明过程或演算步骤）
19. (本小题8.0分)
已知关于x的一元二次方程x2+mx−m−1=0．
(1)求证：无论m取何值，方程总有两个实数根；
(2)若方程有一根为−4，求m的值．
20. (本小题8.0分)
已知二次函数y=x²−4x+3．
(1)直接写出抛物线与x轴交点坐标______、______；与y轴交点坐标______；顶点坐标为______；
(2)在给出的平面直角坐标系xOy中，画出这个二次函数的图象；
(3)当00且m≠0，
解得m>−4且m≠0；
故选：D．
根据根的判别式的意义得到Δ=(−4)2−4m⋅(−1)>0且m≠0，然后解不等式即可．
本题考查了根的判别式：一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2−4ac有如下关系：当Δ>0时，方程有两个不相等的实数根；当Δ=0时，方程有两个相等的实数根；当ΔS乙2，
∴两人射击成绩比较稳定的是乙．
故答案为：乙．
根据方差的意义即方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，数据越稳定，即可得出答案．
此题主要考查了方差的意义和应用，要熟练掌握，解答此题的关键是要明确：方差越大，表明这组数据偏离平均数越大，数据越不稳定；方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，数据越稳定．
11.【答案】1
【解析】解：解方程x2−7x+12=0得，
x1=3，x2=4，
由勾股定理得，斜边为5，
∴此直角三角形的内切圆的半径为=12×(3+4−5)=1，
故答案为：1．
先解一元二次方程，根据勾股定理解得三角形的斜边，利用直角三角形内切圆的半径等于两直角边之和与斜边之差的一半，可得结果．
本题主要考查了因式分解法解一元二次方程，熟记直角三角形内切圆的半径等于两直角边之和与斜边之差的一半是解答此题的关键．
12.【答案】y=2(x−3)2+2
【解析】解：抛物线y=2x2−1的顶点坐标为(0,−1)，
先向右平移3个单位，再向上平移3个单位后的抛物线的顶点坐标为(3,2)，
所以平移后的抛物线的解析式为y=2(x−3)2+2．
故答案为：y=2(x−3)2+2．
先求出平移后抛物线的顶点坐标，再利用抛物线的顶点式写出解析式即可．
本题考查了二次函数图象与几何变换，解题的关键是熟练掌握点的平移规律，并根据规律利用点的变化确定函数解析式．
13.【答案】5
【解析】
【分析】
本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0(a≠0)的两根时，x1+x2=−ba，x1x2=ca．
先根据根与系数的关系得到x1+x2=4，x1x2=1，然后把x1(1+x2)+x2展开得到x1+x2+x1x2，然后利用整体代入的方法计算即可．
【解答】
解：根据题意得x1+x2=4，x1x2=1，
所以x1(1+x2)+x2=x1+x1x2+x2
=x1+x2+x1x2
=4+1
=5．
故答案为5．
14.【答案】−1
【解析】解：把x=−1，y=2和x=0，y=−1代入y=x2+bx+c1−b+c=2c=−1，解得b=−2c=−1，
所以二次函数为y=x2−2x−1，
当x=2时，y=4−4−1=−1，
所以m=−1．
故答案为−1．
先把x=−1，y=2和x=0，y=−1代入二次函数解析式求出b、c，确定二次函数解析式，然后计算出自变量为2的函数值即可．
本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．
15.【答案】54
【解析】解：设该圆锥底面圆的半径为r．
∵每个小方格都是边长为1的正方形，
∴AO=32+42=5，AB=72+12=52，
∵OA2+OB2=AB2，
∴∠AOB=90°，
∴90π×5180=2πr，
∴r=54．
故答案是：54．
利用弧长等于圆锥底面圆的周长这一等量关系即可求解．
本题运用了弧长公式和圆的周长公式，建立准确的等量关系是解题的关键．
16.【答案】无解
【解析】解：把A(−2,4)代入抛物线解析式得：4=4a，即a=1，
把a=1代入得：y=x2，
把A(−2,4)与B(1,1)代入直线解析式得：−2b+c=4b+c=1，
解得：b=−1c=2，即直线解析式为y=−x+2，
可得方程x2+x+2=0，
∵Δ=1−8=−70时，方程有两个不相等的两个实数根；②当Δ=0时，方程有两个相等的两个实数根；③当Δ