
初中数学北师大版七年级上册6.3 数据的表示第3课时教学设计
展开
这是一份初中数学北师大版七年级上册6.3 数据的表示第3课时教学设计,共9页。教案主要包含了教学重难点,教学用具,教学过程设计等内容,欢迎下载使用。
教学目标
1.学会对数据进行分组.
2.明确绘制频数直方图的一般步骤,能绘制频数直方图.
3.经历对数据的分析与处理过程,提高数据处理能力.
4.通过学生收集数据,组织讨论,作出决策的活动,培养学生独立思考,合作交流,敢于发表自己的观点的习惯.
二、教学重难点
重点:明确制作频数直方图的一般步骤,能绘制频数直方图.
难点:对数据进行合理分组.
三、教学用具
电脑、多媒体、课件等
四、教学过程设计
教学环节
教师活动
学生活动
设计意图
环节一
创设情境
【复习回顾】
教师活动:先复习回顾上节课的知识点,再回顾在已知分组的情况下制作频数直方图的方法,通过追问顺势引出本节课需要探讨的主题.
问题:频数直方图是一种特殊的______,它将统计对象的数据进行了_______,画在横轴上,纵轴表示各组数据的_______.
预设答案: 条形统计图;分组;频数
问题:右表是某校七(2)班的同学入学信息表,如何制作班上数学成绩的频数直方图?
预设答案:班上学生数量较多,且数学成绩为连续的数据, 先将数学成绩按照一定的距离分组,统计每个组的学生人数.再根据统计表制作出频数直方图.
追问: 如何对数据进行分组?
回顾、思考并积极回答问题.
回顾频数直方图的相关知识,及在已知分组情况下频数直方图的制作方法,为本节课的学习做好铺垫.
环节二 探究新知
【合作探究】
教师活动:结合实例分析,帮助学生掌握给数据分组的方法,在探索的过程中明确制作频数直方图的一般步骤.
为了了解某地区新生儿体重状况,某医院随机调取了该地区60名新生儿的出生体重,结果(单位:g)如下:
绘制相应的频数直方图,图中反映出该地区新生儿体重状况怎样?
教师强调:当遇到大量的数据或数据连续取值时,我们通常先将数据适当分组,然后再制作频数直方图直观地反映整体的分布状况.
预设答案:
解:(1)确定所给数据的最大值和最小值.上述数据中最大值是4160,最小值是1900;
(2)将数据适当分组.
最大值和最小值相差:4160-1900=2260.
方法一:先定组距再定分组数.
提示:每组两个端点之间的距离叫组距.分组时,应要求各组的组距相等.
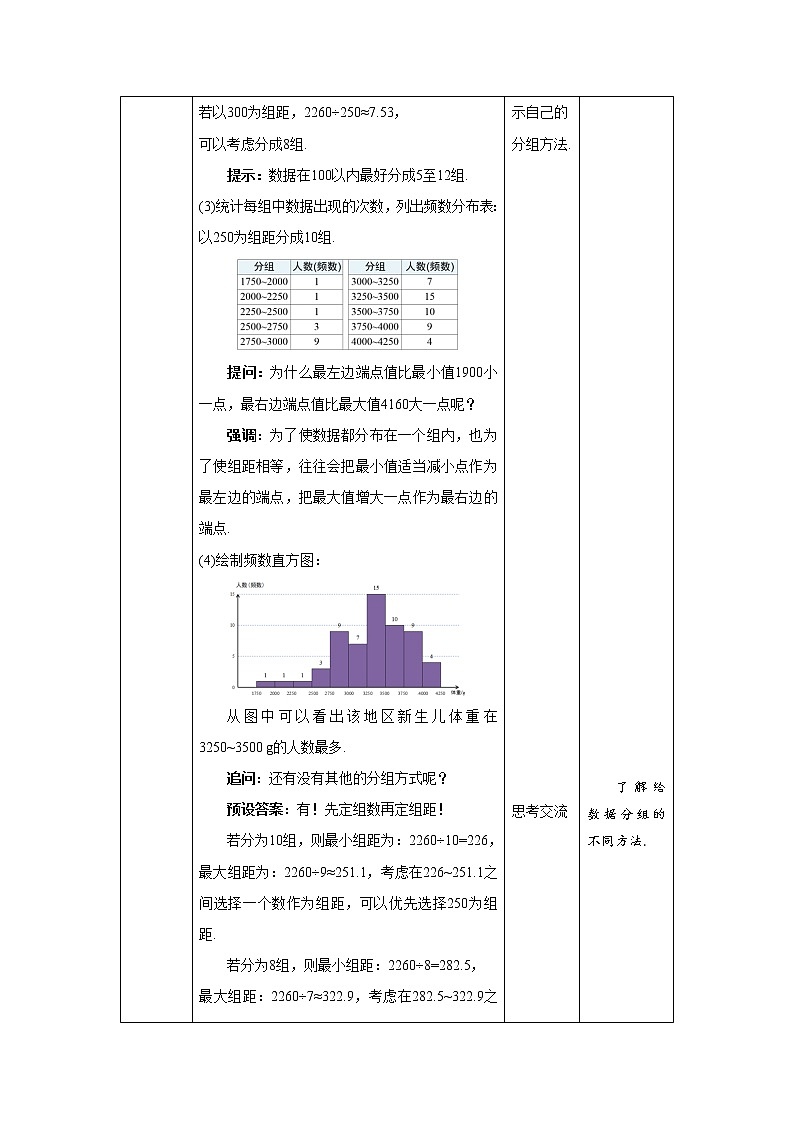
若以250为组距,2260÷250=9.04,
可以考虑分成10组;
若以300为组距,2260÷250≈7.53,
可以考虑分成8组.
提示:数据在100以内最好分成5至12组.
(3)统计每组中数据出现的次数,列出频数分布表:
以250为组距分成10组.
提问:为什么最左边端点值比最小值1900小一点,最右边端点值比最大值4160大一点呢?
强调:为了使数据都分布在一个组内,也为了使组距相等,往往会把最小值适当减小点作为最左边的端点,把最大值增大一点作为最右边的端点.
(4)绘制频数直方图:
从图中可以看出该地区新生儿体重在3250~3500 g的人数最多.
追问:还有没有其他的分组方式呢?
预设答案:有!先定组数再定组距!
若分为10组,则最小组距为:2260÷10=226,
最大组距为:2260÷9≈251.1,考虑在226~251.1之间选择一个数作为组距,可以优先选择250为组距.
若分为8组,则最小组距:2260÷8=282.5,
最大组距:2260÷7≈322.9,考虑在282.5~322.9之间选择一个数作为组距.可以优先选择300为组距.
统计分成8组,以300为组距的每组中数据出现的次数,列出频数分布表:
强调:“~“包含左边的数,不包含右边的数.
如:3000~3300,包含3000,但不包含3300.
绘制频数直方图:
从图中可以看出该地区新生儿体重在3300~3600 g的人数最多.
【归纳】
1.确定组数和组距.可以先定组距,再定组数;也可以先定组数,再定组距.
2.组数和组距的关系:组数=(最大值-最小值)÷组距.
3.数据在100以内最好分成5至12组.
【议一议】
制作频数直方图的大致步骤是什么?
预设答案:
(1)找出所给数据中的最大值和最小值,确定统计量的范围;
(2)确定组数和组距并进行分组,数据个数在100以内,一般分5至12组;
(3)统计每组中数据的频数,列出频数分布表;
(4)根据分组和频数,绘制频数直方图.
【做一做】
测量一下你1 min脉搏跳动的次数.
预设答案:用右手食指和中指按住左手手腕处脉搏,使用教室墙壁上的挂钟计数,从第1秒开始默数自己的脉搏跳动次数,60秒后记下脉搏跳动的总次数.
(通过测试,1 min内我的脉搏跳动的次数为80次.)
(2)汇总全班同学的数据,制作频数直方图,看看大多数同学1 min脉搏跳动的次数处于哪个范围.
汇总班上40名同学在1 min内脉搏跳动的次数如下:
a.数据中最大值是105,最小值是69,两者相差为:105-69=36.
b.使用先定组距再定组数的方法来分组,若考虑以7为组距, 36÷7≈5.14,可以考虑分成6组.
c.统计每组中数据出现的次数,列出如下频数分布表:
d.绘制频数直方图:
从图中可以看出大多数同学1 min脉搏跳动的次数处于93~100次这个范围.
【归纳】
绘制频数直方图的一般步骤
(1)找出所给数据中的最大值和最小值;
(2)确定组数和组距并进行分组;
(3)统计每组中数据的频数,列出频数分布表;
(4)绘制频数直方图.
小组交流、讨论.
各小组展示自己的分组方法.
思考交流
.
记笔记.
交流发言.
小组讨论、制作.
记笔记.
通过对具体实例的分析,帮助学生理解、掌握给数据分组的方法.
掌握组距、分点的概念,得出组距与组数的关系.
了解给数据分组的不同方法.
学会给数据正确分组并绘制频数直方图.
总结出绘制频数直方图的一般步骤.
让学生再次经历统计的过程,进一步感受如何用频数直方图处理连续型数据.
归纳、总结绘制频数直方图的一般步骤.
环节三 应用新知
【典型例题】
让学生先独立思考,可以尝试自己先做一做,教师再进行适当的讲解与整理.
例 通过问卷调查得出某班32位同学出生时的身高的结果(单位:cm)如下:
请将数据适当分组,并绘制相应的频数直方图,看看班上大多数同学出生时的身高处于哪个范围.
预设答案:
分析:分析:先找出这32个数据中的最大值与最小值,算出相差后先定好组距,使用公式:组数=(最大值-最小值)÷组距计算出组数,给数据分好组后统计每组数据出现的频数,列好频数分布表,根据频数分布表绘制出频数直方图后获取相关信息即可.
解:(1)上述数据中:最大值是53,最小值是45,最大值和最小值相差为:53-45=8;
(2)考虑以1.5为组距,8÷1.5≈5.3,可以考虑分为6组;
(3)统计每组中数据出现的次数,列出频数分布表:
(4)绘制频数直方图:
从图中可以看出班上大多数同学出生时的身高在49 cm至50.5 cm范围内.
明确频数直方图的画法.
通过对有关实际问题的解决,进一步掌握绘制频数直方图的方法.
环节四 巩固新知
教师给出练习,随时观察学生完成情况并相应指导,最后给出答案,根据学生完成情况适当分析讲解.
1.已知一组数据,最大值为93,最小值为22,先要把它分成6组,则下列组距合适的是( )
A 9 B 12 C 15 D 18
2.在绘制频数直方图时,计算处最大与最小值的差为25,若取组距为4,则组数为( )
A 4组 B 5组 C 6组 D 7组
3.一组数据的最小数是12,最大数是38,如果分组的组距相等且组距为3,那么分组后的第一组为( )
A 11.5~13.5 B 11.5~14.5
C 12.5~14.5 D 12.5~15.5
4.某班大课间活动抽查了25名学生每分钟的跳绳次数,获得如下数据(单位:次):
请将数据适当分组,并绘制相应的频数直方图.
答案:1.B;2.D;3.B
4.
解析:
1.分析:根据题意,最大值与最小值的差值为:93-22=71,要把它分成6组,已知组数=(最大值-最小值)÷组距,组距=71÷6≈11.8,所以选择12为组距比较合适.答案选 B.
2.分析:根据题意,最大值与最小值的差值为25,已知组数=(最大值-最小值)÷组距,若取组距为4,则组数=25÷4=6.25,所以考虑分为7组比较合适.答案选 D.
3.分析:为了使数据都分布在组内,往往会把最小值适当减小点作为最左边的端点.而题中这组数据的最小数是12,所以第一组数据的最左边端点应小于12,选项C、D错误;已知题中分组的组距相等且组距为3,所以第一组的右侧端点应为:11.5+3=14.5,即第一组的数据范围为:11.5~14.5,答案选B.
4.分析:先找出这25个数据中的最大值与最小值并算出差,定好组距与组数,给数据分好组后统计每组数据出现的频数列出频数分布表,根据频数分布表绘制出相应频数直方图.
解:(1)上述数据中最大值和最小值差值为:133-60=73;
(2)考虑以12为组距,73÷12≈6.1,可以考虑分为7组;
(3)统计每组中数据出现的次数,列出频数分布表:
(4)绘制频数直方图:
自主完成练习,然后集体交流评价.
通过课堂练习进一步突破给数据分组这一难点内容,并考查学生绘制频数直方图的应用能力.
环节五 课堂小结
思维导图的形式呈现本节课的主要内容:
回顾本节课的重点内容
帮助学生巩固本节所学知识.
环节六
布置作业
教科书第174页习题6.5第1题.
课后自主完成.
及时了解学生对本节课知识的掌握情况,以便对本节下一课时进行课前备课.
相关教案
这是一份初中数学人教版九年级下册29.2 三视图第3课时教学设计,共9页。教案主要包含了教学目标,教学重难点,教学用具,教学过程设计等内容,欢迎下载使用。
这是一份初中数学北师大版九年级上册2 视图第3课时教学设计及反思,共7页。教案主要包含了教学目标,教学重难点,教学用具,教学过程设计等内容,欢迎下载使用。
这是一份北师大版九年级上册1 菱形的性质与判定第3课时教案设计,共8页。教案主要包含了教学目标,教学重难点,教学用具,教学过程设计等内容,欢迎下载使用。










