中考数学专项突破之数学思想与方法 课件

这是一份中考数学专项突破之数学思想与方法 课件，共47页。PPT课件主要包含了返回主目录，≤k≤275等内容，欢迎下载使用。

整体思想,就是在研究和解决有关数学问题时,通过研究问题的整体形式、整体结构、整体特征,从而对问题进行整体处理的解题方法.从整体上去认识问题、思考问题,常常能化繁为简、变难为易,同时又能培养学生思维的灵活性、敏捷性.整体思想的主要表现形式包括：整体代入、整体加减、整体代换、整体联想、整体补形、整体改造等.在初中数学中的数与式、方程与不等式、函数与图象、几何与图形等方面,整体思想都有很好的应用,因此,每年的中考中涌现了许多别具创意、独特新颖的涉及整体思想的问题,尤其在考查高层次思维能力和创新意识方面具有独特的作用.
整体是与局部对应的,按常规不容易求某一个(或多个)未知量时,可打破常规,根据题目的结构特征,把一组数或一个代数式看作一个整体,从而使问题得以解决. 整体思想是指把研究对象的某一部分(或全部)看成一个整体,通过观察与分析,找出整体与局部的联系,从而在客观上寻求解决问题的新途径.
若a+b=2,ab= -3,则代数式a3b+2a2b2+ab3的值为　　　　.分析：将原式因式分解,再把已知等式的值代入计算即可求出结果.解析：a3b+2a2b2+ab3=ab(a2+2ab+b2)=ab(a+b)2=-3×22=-12.【高分点拨】对于考查代数式求值的问题,如果代数式中的字母表示的数没有明确告知,而是隐含在题设条件中,首先应将所需求值的代数式进行同类项的合并,或者进行因式分解,再将相同的项或因式的值整体代入即可求出代数式的值. 已知a-3b=3,则6b+2(4-a)的值是　　　　.解析：∵a-3b=3,∴原式=6b+8-2a=-2(a-3b)+8=-6+8=2.
转化思想要求我们居高临下地抓住问题的实质,在遇到较复杂的问题时,能够辩证地分析问题,通过一定的策略和手段,使复杂的问题简单化,陌生的问题熟悉化,抽象的问题具体化. 转化的内涵非常丰富,比如把隐含的数量关系转化为明显的数量关系,把从这一个角度提供的信息转化为从另一个角度提供的信息.
利用转化思想解决问题,常常涉及对已知与未知、数量与图形、图形与图形之间的转化,通过这些元素之间的转化来解决问题.
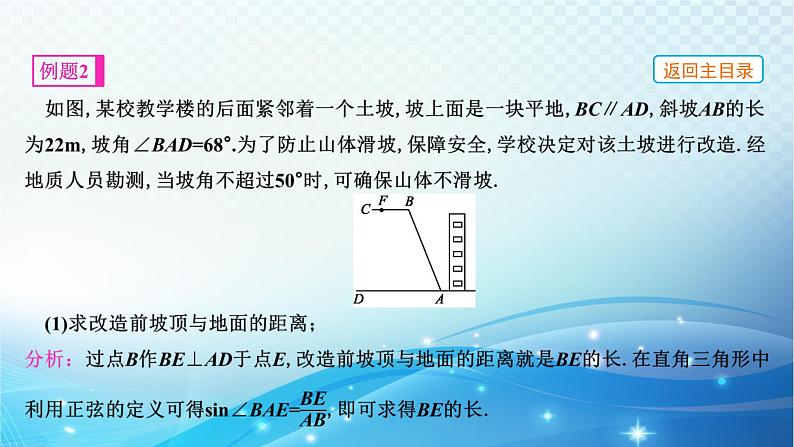
【高分点拨】本题中的转化思想主要体现在把实际的测量问题转化为数学问题、把斜三角形问题转化为直角三角形问题,此类题型属中考常考题型.
方程思想要求我们将问题中的已知量和未知量之间的数量关系通过适当设未知数建立起方程(组),然后通过解方程(组)使问题得到解决的思维方式. 揭示题目中隐含的等量关系,设未知数、构造方程,建立已知与未知的联系,从而使问题得到解决.
在几何计算中,常利用几何中的定理、公式,如勾股定理、垂径定理、三角函数关系等作为等量关系来构造方程,或利用图形中的某些位置关系所隐含的等量关系来构造方程.
当数学问题不能用统一方法处理时,我们可以依据研究对象性质的差异,按照一定的分类方法或标准将问题分为全而不重、广而不漏的若干类,然后逐类分别讨论,再把结论汇总得到问题的答案. 分类讨论题型常与开放探究问题结合在一起,当题目条件给得不明确时,或者情况不唯一时,都需要根据条件分类解决.
在解答分类讨论问题时,首先确定讨论对象的取值范围；其次确定分类标准,做到不重不漏；再对所分的类逐步进行讨论；最后进行归纳小结,综合得出结论.
(2,4)或(3,4)或(8,4)
从现实生活或具体情境中抽象出数学问题,用数学符号建立方程、不等式、函数等,表示数学问题中的数量关系和变化规律,求出结果并讨论结果的意义. 把所考察的实际问题转化为数学问题,构造相应的数学模型,通过对数学模型的研究使实际问题得以解决.
将具体问题数学化是建模的关键,也就是将具体问题中的量首先用字母表示出来,再根据式子所符合的具体数学问题,运用相关的知识进行求解.
跳绳是大家喜闻乐见的一项体育运动,集体跳绳时,需要两人同频甩动绳子,当绳子甩到最高处时,其形状可近似看作抛物线.如图是小明和小亮甩绳子到最高处时的示意图,两人拿绳子的手之间的距离为4 m,离地面的高度为1 m,以小明的手所在位置为原点,建立平面直角坐标系.(1)当身高为1.5 m的小红站在绳子的正下方,且距小明拿绳子手的右侧1 m处时,绳子刚好通过小红的头顶,求绳子所对应的抛物线的解析式；
在水平的地面BD上有两根与地面垂直且长度相等的电线杆AB,CD,以点B为坐标原点,直线BD为x轴建立平面直角坐标系,得到图①.已知电线杆之间电线的形状可近似地看成抛物线y=0.1x2-0.8x+3. (1)求电线最低点离地面的距离；解：∵0.1＞0,∴抛物线的顶点为最低点.由题意y=0.1x2-0.8x+3化为顶点式为y=0.1(x-4)2+1.4,∴电线最低点离地面的距离为1.4米.答：电线最低点离地面的距离为1.4米.
(2)因实际需要,电力公司需要在BD之间增设一根电线杆.①若将电线杆MN增设在距离AB为3米处(如图②),使左边抛物线的最低点离MN为1米,离地面1.8米,求MN的长；解：∵y=0.1x2-0.8x+3,∴A(0,3).由题意得,抛物线F1的顶点坐标为(2,1.8).设F1的解析式为y=a(x-2)2+1.8(a≠0),将(0,3)代入,得4a+1.8=3,解得a=0.3,∴抛物线F1的解析式为y=0.3(x-2)2+1.8.当x=3时,y=0.3×1+1.8=2.1.∴MN的长为2.1米.
②若将一根长为3米的电线杆MN增设在线段BD之间的位置上(如图③),使右边抛物线F2的二次项系数始终是0.25,设电线杆MN距离AB为m米,抛物线F2的最低点离地面的距离为k米,当4≤m≤6时,k的取值范围是　　　　 .解：∵AB=MN=CD=3米,∴右边抛物线F2的顶点一定在MD的垂直平分线上.∵y=0.1x2-0.8x+3=3,∴x1=0或x2=8.∴BD=8米.
5.如图,在△ABC中,BC=AC=5,AB=8,CD为边AB的高,点A在x轴上,点B在y轴上,点C在第一象限,若A从原点出发,沿x轴向右以每秒1个单位长度的速度运动,则点B随之沿y轴下滑,并带动△ABC在平面内滑动,设运动时间为t秒,当B到达原点时停止运动.(1)连接OC,线段OC的长随t的变化而变化,当OC最大时,t=　　　　； 解析：∵BC=AC=5,AB=8,CD⊥AB,∴BD=4=AD,∴由勾股定理得CD=3.