2022-2023学年山西省朔州市七年级（上）期末数学试卷（A卷）（含解析）

这是一份2022-2023学年山西省朔州市七年级（上）期末数学试卷（A卷）（含解析），共15页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1. 数轴上点P表示的数为−2，与点P距离为3个单位长度的点表示的数为( )
A. 1B. 5C. 1或−5D. 1或5
2. 一方有难八方支援，各省市都斥资到抗疫前线，据有关部门初步统计，国家已经投入资金1390亿元抗疫防控，这个数据的背后不仅是抗击疫情的强力保障，更是祖国综合实力的直接体现，为此很多人高呼：此生无悔入华夏，来世再做中国人，将139000000000用科学记数法表示为( )
A. 1.39×108B. 1.39×109C. 1.39×1010D. 1.39×1011
3. 下列说法中，正确的是( )
A. 单项式−3a2bc的次数是2
B. 代数式2ab−ab2+3c−1是三次四项式
C. 单项式−12abc的系数是−12，次数是1
D. −2不是单项式
4. 教材中“整式的加减”一章的知识结构如图所示，则A和B分别代表的是( )
A. 整式，合并同类项B. 单项式，合并同类项
C. 系数，次数D. 多项式，合并同类项
5. 下列计算正确的是( )
A. 3a2+2a2=5a4B. −2(a+b)=−2a+2b
C. 6xy−x=6yD. −a2b+2a2b=a2b
6. 如图，已知B，C是线段AD上任意两点，E是AB的中点，F是CD的中点，下列结论不正确的是( )
A. AC=CDB. AB=2AE
C. CF=12CDD. BC=EF−AE−FD
7. 如图所示，∠AOC=90°，点B，O，D在同一直线上，若∠1=28°，则∠2的度数为( )
A. 118°
B. 108°
C. 62°
D. 152°
8. 解方程2x+13=1−x−12，去分母正确的是( )
A. 2(2x+1)=1−3(x−1)B. 2(2x+1)=6−3x−3
C. 2(2x+1)=6−3(x−1)D. 3(2x+1)=6−2(x−1)
9. 如图，把半径为1的圆放到数轴上，圆上一点A与表示−1的点重合，圆沿着数轴滚动一周，此时点A表示的数是( )
A. −1+2πB. −1+π
C. −1+2π或−1−2πD. −1+π或−1−π
10. 《九章算术》中有这样一道数学问题，原文如下：清明游园，共坐八船，大船满六，小船满四，三十八学子，满船坐观.请问客家，大小几船？其大意为：清明时节出去游园，所有人共坐了8只船，大船每只坐6人，小船每只坐4人，38人刚好坐满，问：大小船各有几只？若设有x只小船，则可列方程为( )
A. 6x+4(8−x)=38B. 4x+6(8−x)=38
C. 4x+6x=38D. 8x+6x=38
二、填空题（本大题共5小题，共15.0分）
11. −(+16)的相反数是 ．
12. 若代数式x2+3x的值为5，则代数式2x2+6x−9的值为______．
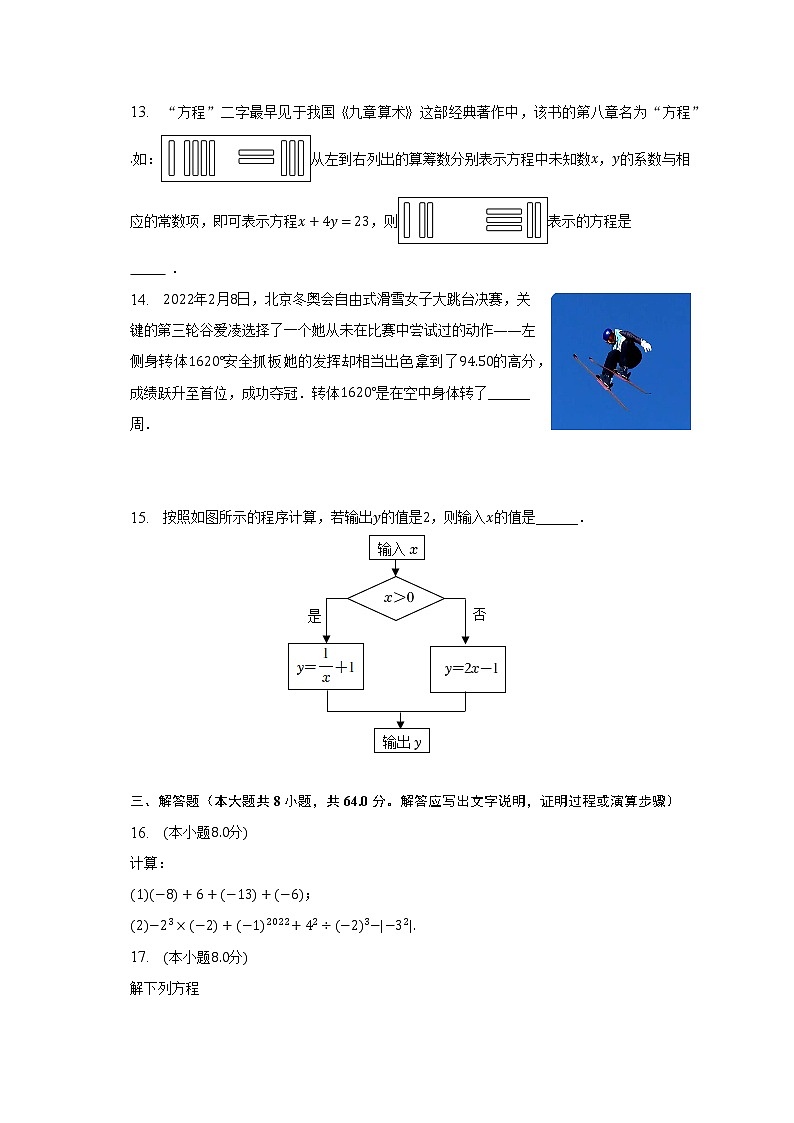
13. “方程”二字最早见于我国《九章算术》这部经典著作中，该书的第八章名为“方程”.如：从左到右列出的算筹数分别表示方程中未知数x，y的系数与相应的常数项，即可表示方程x+4y=23，则表示的方程是 ．
14. 2022年2月8日，北京冬奥会自由式滑雪女子大跳台决赛，关键的第三轮谷爱凌选择了一个她从未在比赛中尝试过的动作——左侧身转体1620°安全抓板，她的发挥却相当出色，拿到了94.50的高分，成绩跃升至首位，成功夺冠．转体1620°是在空中身体转了______周．
15. 按照如图所示的程序计算，若输出y的值是2，则输入x的值是______．
三、解答题（本大题共8小题，共64.0分。解答应写出文字说明，证明过程或演算步骤）
16. (本小题8.0分)
计算：
(1)(−8)+6+(−13)+(−6)；
(2)−23×(−2)+(−1)2022+42÷(−2)3−|−32|.
17. (本小题8.0分)
解下列方程
(1)10x+7=14x−5；
(2)2x−13−10x−16=2x+14−1．
18. (本小题8.0分)
小明在计算多项式M减去多项式2x2y−3xy+1时，误计算成加上这个多项式，结果得到答案2x2y−xy．
(1)请你帮小明求出多项式M；
(2)对于(1)中的多项式M，当x=−1，y=2时，求多项式M的值．
19. (本小题8.0分)
出租车司机李师傅从上午8：00～9：15在大厦至会展中心的东西走向路上营运.共连续运载十批乘客，若规定向东为正，向西为负，李师傅运载这十批乘客的里程如下(单位：千米)：+8，−6，+3，−7，+8，+4，−7，−4，+3，+4．
(1)将最后一批乘客送到目的地时，李师傅在第一批乘客出发地的东边还是西边？相距多少千米？
(2)上午8：00−9：15李师傅开车行驶的路程是多少？
20. (本小题8.0分)
阅读感悟：
数学课上，老师给出了如下问题：
如图1，一条直线上有A、B、C、D四点，线段AB=8cm，点C为线段AB的中点，线段BD=2.5cm，请你补全图形，并求CD的长度．
以下是小华的解答过程：
解：如图2，
因为线段AB=8cm，点C为线段AB的中点，
所以BC=______AB=______cm．
因为BD=2.5cm，
所以CD=BC−BD=______cm．
小斌说：我觉得这个题应该有两种情况，小华只考虑了点D在线段AB上，事实上，点D还可以在线段AB的延长线上．
完成以下问题：
(1)请填空：将小华的解答过程补充完整；
(2)根据小斌的想法，请你在备图中画出另一种情况对应的示意图，并求出此时CD的长度．
21. (本小题8.0分)
为了迎接世界杯足球赛的到来，足球协会举办了一次足球赛，其中得分规则及奖励方案如表：
当比赛进行到每队比赛完12场时，A队共积分20分，并且没有负一场．
(1)试判断A队胜、平各几场？
(2)每赛一场，A队每名队员均得出场费500元，那么比赛完12场后，A队每名队员所得奖金与出场费累计为多少元？
22. (本小题8.0分)
为了节约水资源，某地区对居民用水实行阶梯水价制度，将居民全年用水量(取整数)划分为三档，标准如表：
如该地某户全年用水量为250立方米．则其应缴全年综合水费(含水费、水资源费、污水处理费)合计为180×5+(250−180)×7=1390(元)．
(1)如该地某户全年用水量为300立方米．则其应缴全年综合水费(含水费、水资源费、污水处理费)合计为多少元？
(2)如该地某户缴纳全年综合水费(含水费、水资源费、污水处理费)1180元，求该户全年用水量是多少立方米？
23. (本小题8.0分)
将一副三角板中的含有60°角的三角板的顶点和另一块的45°角的顶点重合于一点O，绕着点O旋转60°的三角板，拼成如图的情况(OB在∠COD内部)，请回答问题：
(1)如图1放置，将含有60°角的一边与45°角的一边重合，求出此时∠AOD的度数．
(2)绕着点O，转动三角板AOB，恰好是OB平分∠COD，此时∠AOD的度数应该是多少？
(3)是否存在这种情况，∠AOC的度数恰好等于∠BOD度数的3倍．如果存在，请求出∠AOD的度数，如果不存在请说明理由．
答案和解析
1.【答案】C
【解析】解：如图：

根据数轴可以得到在数轴上与点P距离3个长度单位的点所表示的数是：−5或1．
故选：C．
在数轴上表示出P点，找到与点P距离3个长度单位的点所表示的数即可．此类题注意两种情况：要求的点可以在已知点−2的左侧或右侧．
此题主要考查了数轴，用几何方法借助数轴来求解，非常直观，且不容易遗漏，体现了数形结合的优点．
2.【答案】D
【解析】解：139000000000=1.39×1011．
故选：D．
科学记数法的表示形式为a×10n的形式，其中1≤|a|